
- •2. Пәннің қысқаша сипаттамасы
- •Осы процестерді қайталау арқылы
- •Осы сияқты екінші және төртінші теңдіктерден
- •Сонымен
- •Сонымен қатар
- •Бұл әдісті кейде “Чебышевтің тиімді итерациялық әдісі ” деп те атайды.
- •Біздің негізгі мақсатымыз берілген үшін -ға минимум беретін параметрлерін табу керек болғандықтан, кесіндісінде анықталған
- •Бөлшектеу әдісі.
- •Итерациялық процестің жалпы қойылуы және сығу принципі.
- •3.Парабола әдісі. (Симпсон формуласы).
- •1. Эйлер әдісі
- •2. Жетілдірілген Эйлер әдісі.
- •3. Рунге –Кутт әдісі. Берілген
- •4.Адамстың экстраполяциялық әдiсi.
- •5. Адамстың интерполяциялық әдісі .
- •1. Тор және торлық функциялар
- •1. Бір өлшемді кеңістіктегі тор және торлық функция.
- •2. Екі өлшемдегі кеңістіктегі тор және торлық функция.
- •2. Жай дифференциалдық операторларды жуықтау
- •Операторын торлық функциялармен алмастыру.
- •Операторын торлық функциялармен алмастыру .
- •Тейлор формуласы бойынша
- •4. Операторын торлық функциямен алмастыру.
- •§3. Шекаралық есептерді жуықтау
- •Жай дифференциалдық теңдеудің Коши есебі:
- •2. Бір ретті дифференциалды теңдеулер жүйесіне қойылған Коши есебі:
- •Шекаралық есеп. (Дирихле есебі)
- •5. Жылу өткішгіштік теңдеуіне қойылған аралас шекаралық есеп
- •Туралы түсінік
- •5.Айырымдық схеманың орнықтылығы туралы түсінік
- •Жәй дифференциалды теңдеулерді шешу. Жетілдірілген Эйлер әдісі.
- •Рунге-Кутт әдісі.
- •Айырымдық схемалардың негізгі түсініктері.
- •Айрымдық схемалардың орнықтылығын зерттеу.
- •Айырымдық есептің жинақталуы .
- •Екінші ретті жай дифференциалдық теңдеулердің шекаралық есебін шешу әдістері
- •Тапсырмалар
- •Глоссари
Туралы түсінік
![]()
Айталық,
![]() облысында сызықты дифференциалды теңдеу
облысында сызықты дифференциалды теңдеу
![]() (4.1)
(4.1)
және оның қосымша шарты
![]() (4.2)
(4.2)
берілсін.
Мұнда
![]() берілген функциялар ,
берілген функциялар ,
![]() сызықты
дифференциалды оператор. (4.1)-(4.2) есебінің
бір ғана шешуі бар деп ұйғарамыз. Енді
сызықты
дифференциалды оператор. (4.1)-(4.2) есебінің
бір ғана шешуі бар деп ұйғарамыз. Енді
![]() облысын
облысын
![]() торымен жабайық.
түйіндердің
тығыздығын анықтайтын параметр болсын.
(4.1)-(4.2) есебін
торымен жабайық.
түйіндердің
тығыздығын анықтайтын параметр болсын.
(4.1)-(4.2) есебін
![]() ,
(4.3)
,
(4.3)
![]() (4.4)
(4.4)
айырымдық
есебімен алмастырайық. Мұндағы
![]() белгілі торлық функциялар. (4.3)-(4.4)
есебінің шешуі
белгілі торлық функциялар. (4.3)-(4.4)
есебінің шешуі
![]() торында анықталған торлық функция.
параметрін өзгерту арқылы, яғни
торында анықталған торлық функция.
параметрін өзгерту арқылы, яғни
![]() торының тығыздығын өзгерту арқылы
(4.3)-(4.4) есебінің
тан
тәуелді шешулерінің
торының тығыздығын өзгерту арқылы
(4.3)-(4.4) есебінің
тан
тәуелді шешулерінің
![]() жиынын аламыз.
жиынын аламыз.
(4.1)-(4.2)
есебінің шешуін (4.3)-(4.4) есебінің шешуі
қаншалықты жуықтайтындығын
![]() -торлық
функциялар кеңістігінде қарастырамыз.
-торлық
функциялар кеңістігінде қарастырамыз.
Айталық,
![]() функциясының
функциясының
![]() торының түйіндеріндегі, яғни
торының түйіндеріндегі, яғни
![]() болсын.
болсын.
Енді айырымдық схеманың шешуінің дәлдігін былай белгілесек:
![]() ,
(4.5)
,
(4.5)
![]() (4.6)
(4.6)
есебін аламыз. Мұндағы
![]()
шамалары жуықтау қателігі (апроксимация қателігі). Яғни (4.1)-(4.2) есебін (4.3)-(4.4) есебімен алмастырғандағы жіберілген қате.
Енді
![]() шамаларын бағалау үшін оларды тиісінше
шамаларын бағалау үшін оларды тиісінше
![]() шекті өлшемді торлық функциялар жиынында
жатады деп есептеп, осы жиындарда
шекті өлшемді торлық функциялар жиынында
жатады деп есептеп, осы жиындарда
![]() нормаларын енгізейік.
нормаларын енгізейік.
Анықтама-1
Егер
![]() шарттары орындалса, онда (4.3)-(4.4)
айырымдық схемасы (4.1)-(4.2) есебіноның
шешуінде
тың
шарттары орындалса, онда (4.3)-(4.4)
айырымдық схемасы (4.1)-(4.2) есебіноның
шешуінде
тың
![]() дәрежесіндегі дәлдікпен жуықтайды
(аппроксимациялайды) дейді. Мұндағы
дәрежесіндегі дәлдікпен жуықтайды
(аппроксимациялайды) дейді. Мұндағы
![]()
Анықтама-2.
Егер
![]() нөлге ұмтылғанда
нөлге ұмтылғанда
![]() нөлге ұмтылса, онда (4.3)-(4.4) есебінің
шешуі (4.1)-(4.2) есебінің шешуіне жинақталады
дейміз. Егер жеткілікті аз шама
нөлге ұмтылса, онда (4.3)-(4.4) есебінің
шешуі (4.1)-(4.2) есебінің шешуіне жинақталады
дейміз. Егер жеткілікті аз шама
![]() табылып, және
табылып, және
![]() болғанда
болғанда
![]() бағалауы орындалса, онда айырымдық
схеманың шешуі
бағалауы орындалса, онда айырымдық
схеманың шешуі
![]() жылдамдықпен
(4.1)-(4.2) есебінің шешуіне жинақталады
дейді немесе айырымдық схеманың дәлдігі
-ге
тең дейді. Мұндағы
жылдамдықпен
(4.1)-(4.2) есебінің шешуіне жинақталады
дейді немесе айырымдық схеманың дәлдігі
-ге
тең дейді. Мұндағы
![]() -тан
тәуелсіз сан.
-тан
тәуелсіз сан.
Кейде
(4.3)-(4.4) есебін
![]() функциясының шекаралық (шеткі) нүктелердегі
белгілі мәндерін теңдіктің оң жағына
шығару арқылы,
функциясының шекаралық (шеткі) нүктелердегі
белгілі мәндерін теңдіктің оң жағына
шығару арқылы,
![]() (4.7)
(4.7)
түрінде жазуға болады. Бұл жағдайда айырымдық схеманың жуықтау қателігін былайша жазады:
![]()
Ал
![]()
теңдігін ретті жуықтау қателігі (аппроксимациясы) дейміз.
5.Айырымдық схеманың орнықтылығы туралы түсінік
1-анықтама.
Егер
![]() сандары табылып,
сандары табылып,
![]() орындалғанда кез-келген
орындалғанда кез-келген
![]() үшін
үшін
![]() (5.1)
(5.1)
айырымдық есебінің бір ғана шешуі бар болып,
![]() (5.2)
(5.2)
теңсіздігі орындалса, онда
![]() (5.3)
(5.3)
айырымдық
схемасын орнықты дейміз. Мұндағы
![]() тан
тәуелсіз тұрақты сан.
тан
тәуелсіз тұрақты сан.
(5.2)
теңсіздігі (5.3) айырымдық схемасының оң
жағына
![]() өсімше берсек, онда оның шешуі
бойынша бірқалыпты
өсімше берсек, онда оның шешуі
бойынша бірқалыпты
аз шамаға өзгеретінін көрсетеді.
Егер
![]() операторы
-ты
операторы
-ты
![]() қа
кескіндейтін сызықты оператор болса,
онда жоғарғы анықтамаға пара-пар мына
анықтаманы беруге болады.
қа
кескіндейтін сызықты оператор болса,
онда жоғарғы анықтамаға пара-пар мына
анықтаманы беруге болады.
2-анықтама.
Егер кез-келген
![]() үшін
сызықты айырымдық есебінің бір ғана
шешуі-
үшін
сызықты айырымдық есебінің бір ғана
шешуі-![]() бар болып,
бар болып,
![]() (5.4)
(5.4)
теңсіздігі орындалса, онда айырымдық есепті орнықты дейміз.
Айталық,
(6.1)
айырымдық схемасы
![]() (6.2)
(6.2)
шекаралық
есебін
![]() шешуі бойынша
шешуі бойынша
![]() дәлдікпен жуықтайтын болсын. Яғни (6.2)
теңдеуінің шешуін (6.1) теңдеуіне қойсақ,
онда
дәлдікпен жуықтайтын болсын. Яғни (6.2)
теңдеуінің шешуін (6.1) теңдеуіне қойсақ,
онда
![]()
Осыдан
![]() .
(6.3)
.
(6.3)
Мұндағы
![]() тан
тәуелсіз тұрақты сан. Енді (6.1) айырымдық
есебінің жуықтау дәлдігімен оның
орнықтылығының және
шешуінің (6.2) теңдеуінің шешуіне
жинақталуының арасындағы байланысы,
яғни жуықтау дәлдігі мен орнықтылықтан
жинақтылық шарты орындалатынын көрсететін
теореманы берейік.
тан
тәуелсіз тұрақты сан. Енді (6.1) айырымдық
есебінің жуықтау дәлдігімен оның
орнықтылығының және
шешуінің (6.2) теңдеуінің шешуіне
жинақталуының арасындағы байланысы,
яғни жуықтау дәлдігі мен орнықтылықтан
жинақтылық шарты орындалатынын көрсететін
теореманы берейік.
Теорема.
айырымдық схемасы
![]() есебін
дәлдікпен жуықтайтын және орнықты
болса, онда
шешуі
есебін
дәлдікпен жуықтайтын және орнықты
болса, онда
шешуі
![]() шешуіне жинақталады және
шешуіне жинақталады және
![]() (6.4)
(6.4)
бағалауы орындалады.
Қорытындысында мынаны ескерген жөн:
1.
сызықты айырымдық есебінің шешуі
![]() теңдеуінің шешуіне жинақталатынын
тексеру үшін
теңдеуінің шешуіне жинақталатынын
тексеру үшін
![]() теңдеуінің орнықтылығымен жуықтау
дәлдігін анықтау жеткілікті. Мұнда
есебі тек дифференциалды теңдеудің
шекарадық есебі емес, кез-келген
функционалды теңдеу болуы мүмкін. Ол
тек
айырымдық есебінің конструкциясын
жасау үшін ғана қажетті
теңдеуінің орнықтылығымен жуықтау
дәлдігін анықтау жеткілікті. Мұнда
есебі тек дифференциалды теңдеудің
шекарадық есебі емес, кез-келген
функционалды теңдеу болуы мүмкін. Ол
тек
айырымдық есебінің конструкциясын
жасау үшін ғана қажетті
Зертханалық және студиялық сабақтарды орындаудың нұсқаулығы
№1 Лабораториялық жұмыстар.
Тапсырма: Өрнектерді есептеңіздер және жіберілген қателерді аңықтаңыздар.
1)
![]() 2)
2)
![]() егер
егер
![]()
3)
![]() 4)
4)
![]() егер
егер
![]()
5)
![]() 6)
6)
![]() егер
егер
![]()
7)
![]() 8)
8)
![]() егер
егер
![]()
9)
![]() 10)
10)
![]() егер
егер
![]()
11)
![]() 12)
12)
![]() егер
егер
![]()
14)![]() 15)
15)
![]() егер
егер
![]()
№2 Лабораториялық жұмыстар
1-тапсырма: Таблица арқылы берілген функцияның Лагранж формуласы арқылы нүктесіндегі мәнін табыңыз:
2-тапсырма:
Лагранж
көпмүшесін есептеудің программасын
құрыңыз және осы программаның көмегімен
![]() функциясының мәндерін-
функциясының мәндерін-![]() пайдаланып
пайдаланып
![]() нүктесіндегі мәнін табыңыз. (x-тің мәнін
өздеріңіз алыңыздар)
нүктесіндегі мәнін табыңыз. (x-тің мәнін
өздеріңіз алыңыздар)
Сонымен қоса жіберілген қатені есептеп шығарыңыздар.
Таблица №1
-


Варианттың
номері
0.43
1.63597
1
0.5
0.48
1.73234
13
0.6
0.55
1.87686
15
0.55
0.62
2.03345
7
0.65
0.70
2.22846
9
0.45
Таблица №2
-
Варианттың
номері
0.02
1.02316
6
0.03
0.08
1.09590
8
0.05
0.12
1.14725
12
0.1
0.17
1.21483
14
0.15
0.23
1.30120
4
0.20
Таблица №3
-
Варианттың
номері
0.41
2.57418
2
0.4
0.46
2.32513
3
0.5
0.52
2.09336
5
0.55
0.60
1.86203
10
0.45
0.65
1.74926
11
0.65
№3 Лабораториялық жұмыстар.
1-тапсырма. Гаусс әдісін пайдаланып теңдеулер жүйесін шешініздер және қаншалықты дәлдікпен шешкендеріңді анықтандар.
№ 1 № 2
4,24x1+2,73x2-1,55x3=1,87 0,43x1+1,24x2-0,58x3=2,71
2,34x1+1,27x2+3,15x3=2,16 0,74x1+0,83x2+1,17x3=1,26
3,05x1-1,05x2-0,63x3=-1,25 1,43x1-1,58x2+0,83x3=1,03
№ 3 № 4
0,43x1+0,63x2+1,44x3=2,18 1,24x1+0,62x2-0,95x3=1,43
1,64x1-0,83x2-2,45x3=1,84 2,15x1-1,18x2+0,57x3=2,43
0,58x1+1,55x2+3,18x3=0,74 1,72x1-0,83x2+1,57x3=3,88
№ 5 № 6
0,62x1+0,56x2-0,43x3=1,16 1,06x1+0,34x2+1,26x3=1,17
1,32x1-0,88x2+1,76x3=2,07 2,54x1-1,16x2+0,55x3=2,23
0,73x1+1,42x2-0,34x3=2,18 1,34x1-0,47x2-0,83x3=3,26
№ 7 № 8
3,15x1-1,72x2-1,23x3=2,15 1,73x1-0,83x2+1,82x3=0,36
0,72x1+0,67x2+1,18x3=1,43 0,27x1+0,53x2-0,64x3=1,23 2,57x1-1,34x2-0,68x3=1,03 0,56x1-0,48x2+1,95x3=-0,76
№ 9 № 10
0,95x1+0,72x2-1,14x3=2,15 2,18x1+1,72x2-0,93x3=1,06
0,63x1+0,24x2+0,38x3=0,74 1,42x1+0,18x2+1,12x3=1,07
1,23x1-1,08x2-1,16x3=0,97 0,92x1-1,14x2-2,53x3=-0,45
№ 11 № 12
2,23x1-0,73x2+1,27x3=2,43 0,65x1-0,93x2+0,45x3=-0,72
2,15x1+3,17x2-1,43x3=-0,73 1,15x1+0,43x2-0,72x3=1,24
0,83x1+0,72x2+2,12x3=1,42 0,56x1-0,18x2+1,03x3=2,15
№ 13 № 14
1,16x1-0,28x2+2,16x3=1,60 2,16x1-2,83x2+1,15x3=2,32
0,65x1+0,76x2-1,18x3=0,28 1,71x1+2,17x2-0,83x3=1,25
0,53x1+1,07x2-0,63x3=1,27 0,35x1-0,72x2+1,03x3=0,82
№ 15 № 16
1,02x1+0,72x2-0,65x3=1,27 0,53x1-1,63x2-0,76x3=2,18
0,74x1-1,24x2-1,73x3=0,77 0,86x1+1,17x2+1,84x3=1,95
1,78x1+2,32x2+0,74x3=1,16 0,32x1-0,65x2+1,11x3=-0,47
2-тапсырма. Циклді қуалау әдісін пайдаланып
а 1-b 1+c n=f1
а і+1-b і+c і-1=f1 (і=2,3,...,n-1)
а 1-b n+c n-1=fn
теңдеулер жүйесін программа құру арқылы шешіңіздер.
3-тапсырма. Гаусс әдісі арқылы 1-тапсырмадағы теңдеулер жүйесіндегі матрицаның кері матрицасын табыңыздар.
№ 4 Лабораториялық жұмыстар.
1-тапсырма. Біртіндеп жуықтау әдісін қолданып мына теңдеулер жүйесін берілген дәлдікпен шешіңіздер және

формуласын пайдаланып дәлдік -ның қандай мәнінде орындалатының анықтаныздар.
№1 №2


№3 №4
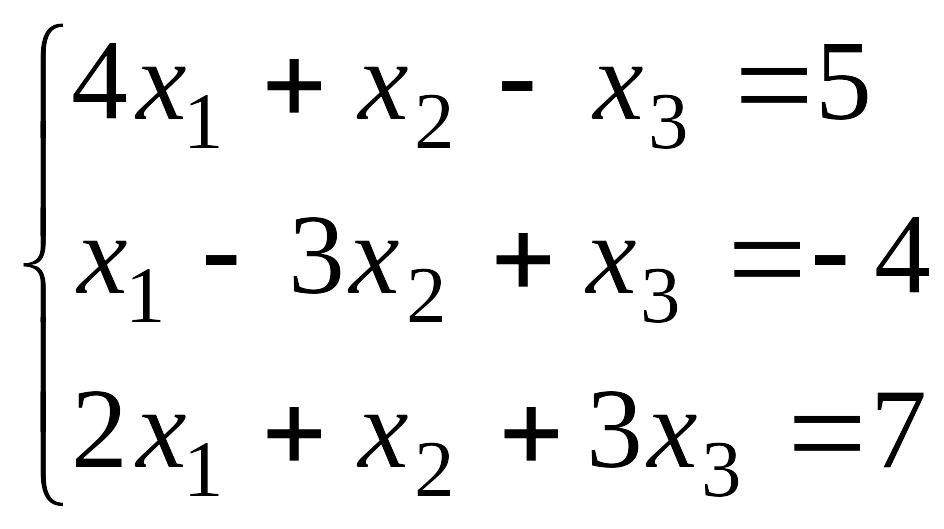

№5 №6

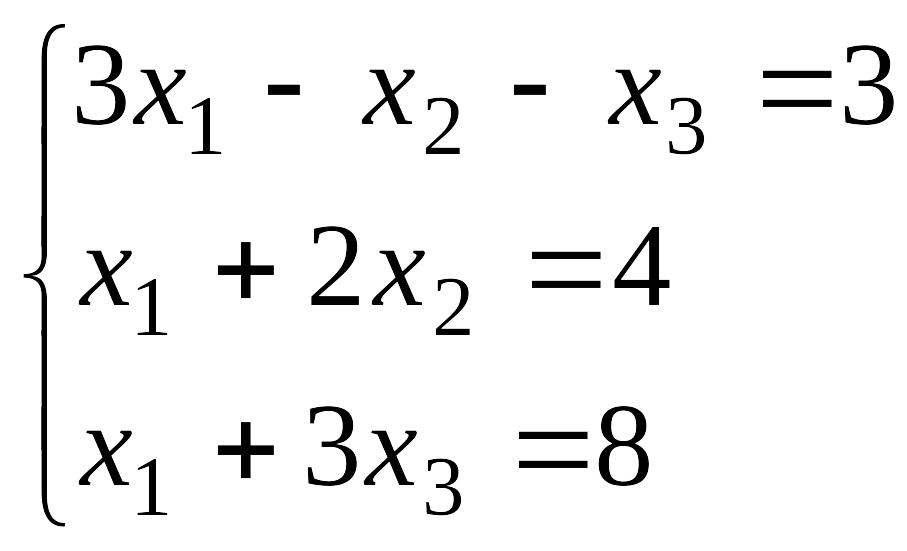
№7 №8


№9 №10
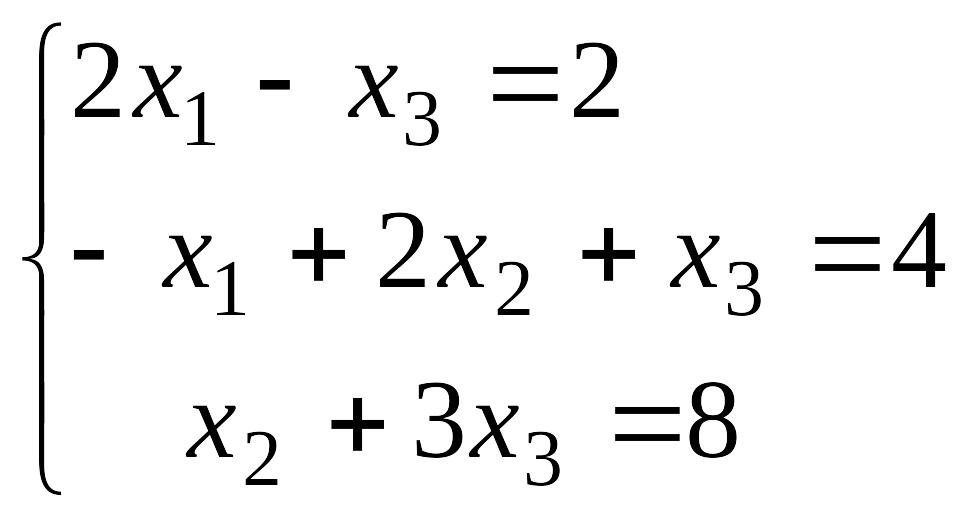
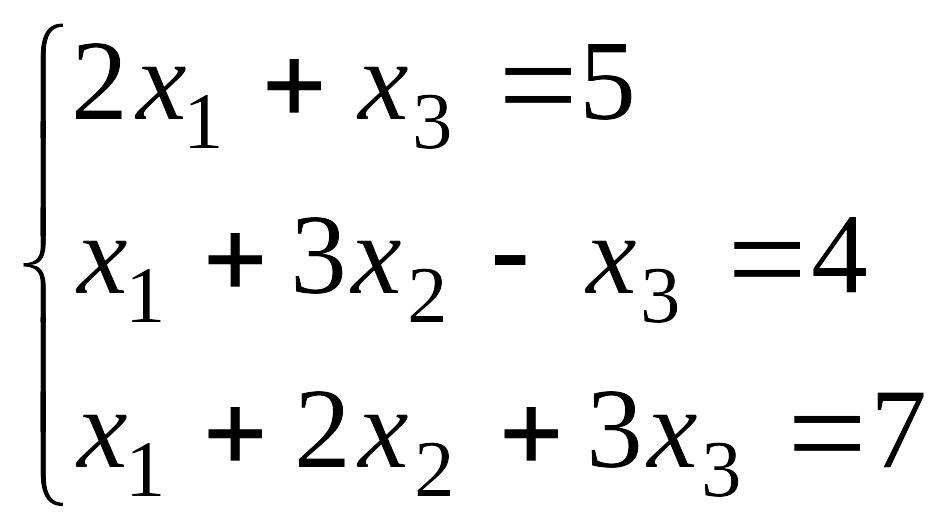
№11 №12

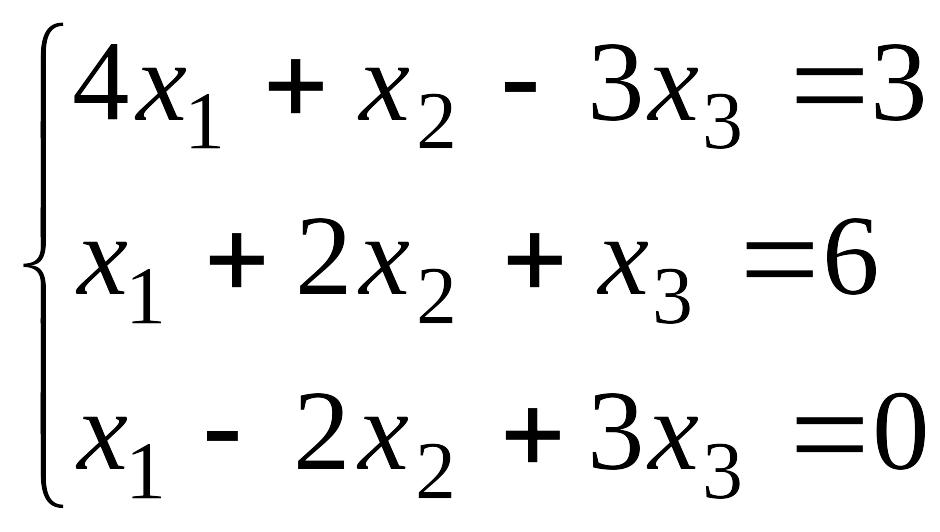
№13 №14
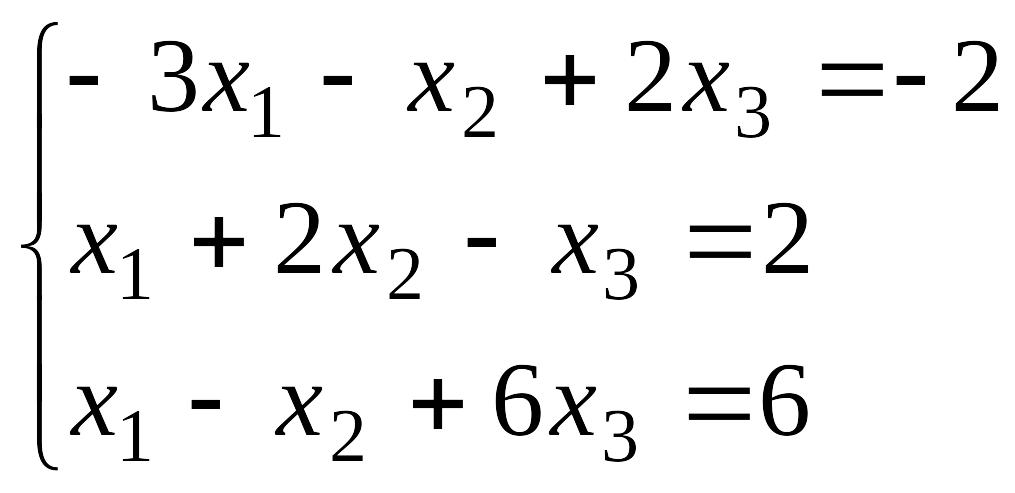

№15 №16


1-тапсырма. 8- параграфтарда көрсетілген әдістерге программа құрыңыздар.
2-тапсырма. 6- параграфтағы лабораториялық жұмыстарда көрсетілген теңдеулер жүйесін градиентті итерациялық әдіс арқылы шешіңіздер.
№ 5 Лабораториялық жұмыстар.
1-тапсырма. Хорда, Ньютон єдістері арќылы тењдеулерді 0,01 дєлдікпен шешіњіздер.
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]() 9.
9.
![]()
10.
![]() 11.
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]() 15.
15.
![]()
№ 6 Лабораториялық жұмыстар.
1. тапсырма интегралды тіктөртбұрыш әдісімен есептеу программасын жаз.
1.1)
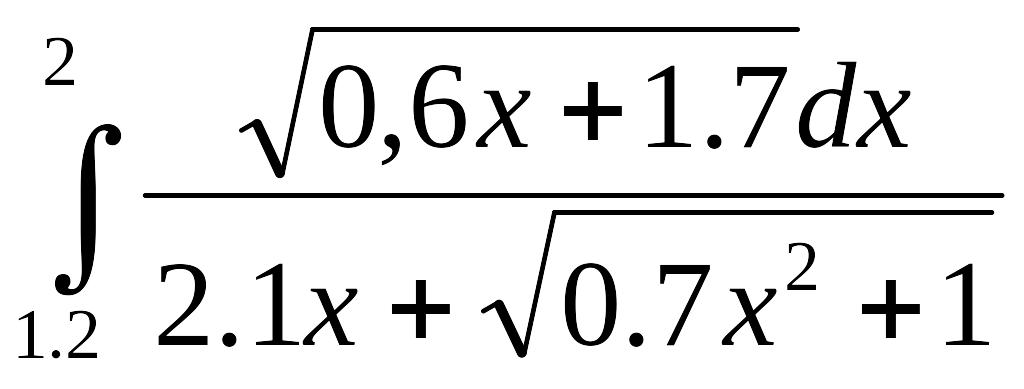 ;
2)
;
2)
 ;
;
3)
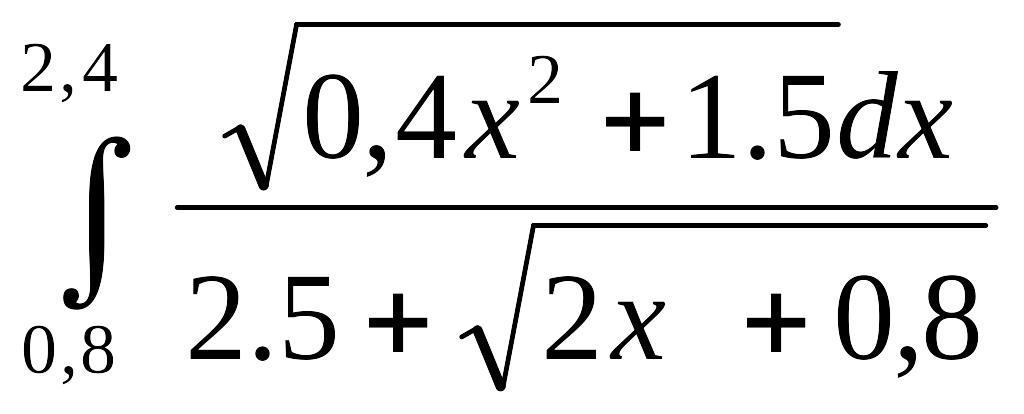 ;
4)
;
4)
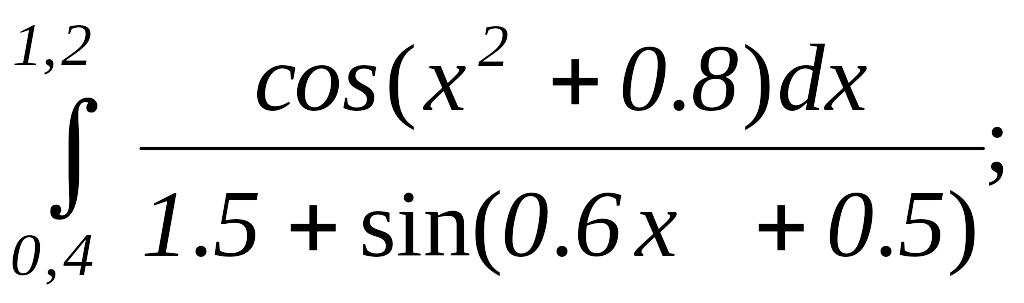 ;
;
5)
 ;
6)
;
6)

7)
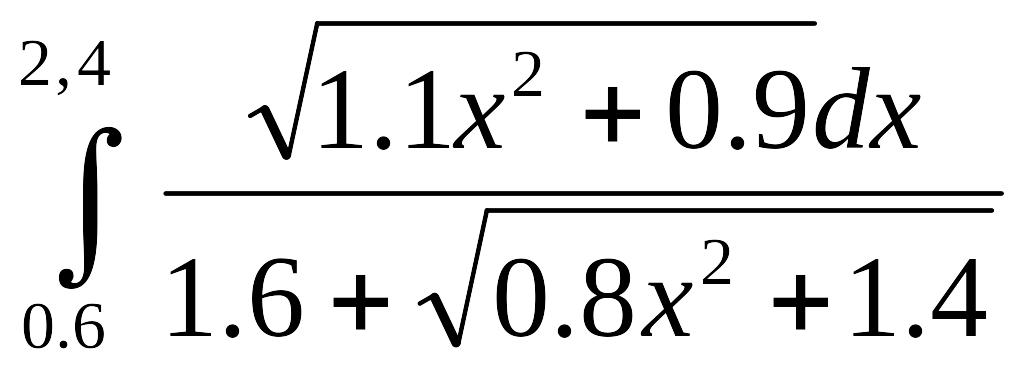 ;
8)
;
8)

9)
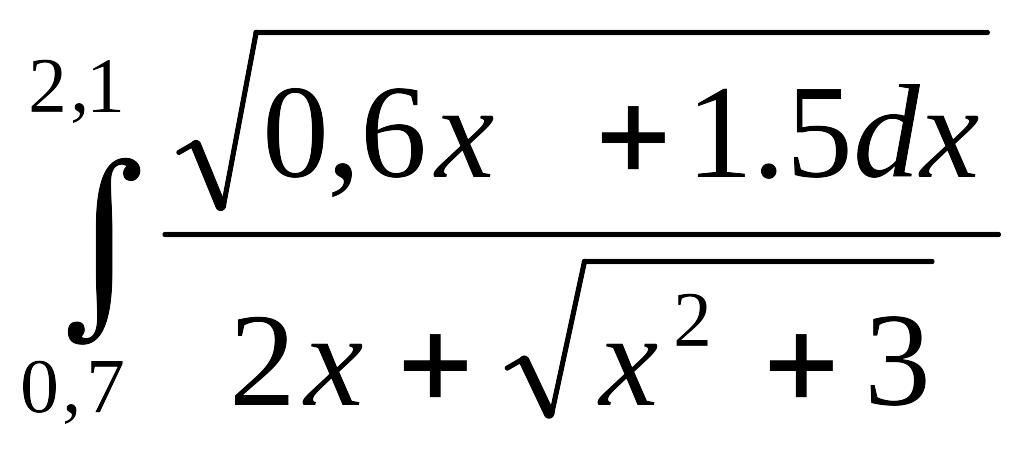 ;
10)
;
10)
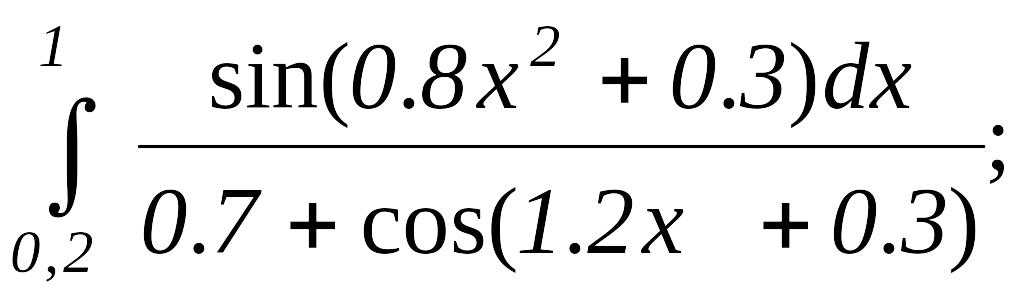
11)
 ;
12)
;
12)

13)
 ;
14)
;
14)
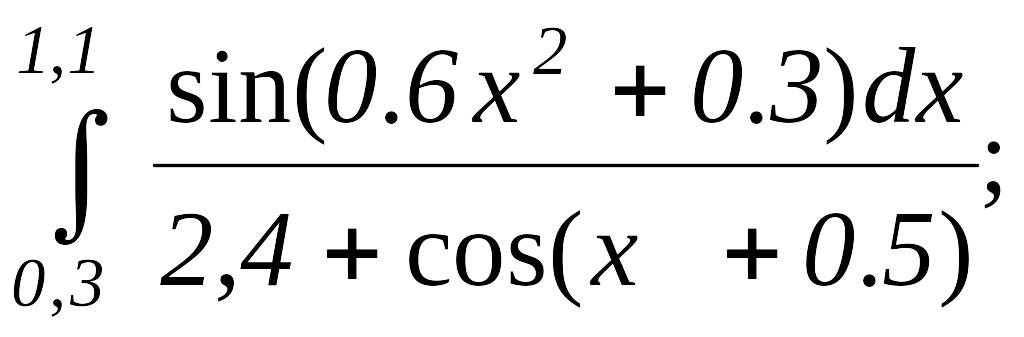
1)Интегралды трапеция әдісімен шығар.
2)Интегралды Симпсон әдісімен шығар.
№7 Лабораториялық жұмыстар.
