§3. Шекаралық есептерді жуықтау
(Айырымдық есептерді қою)
Айталық, дифференциалдық теңдеу
,
,
(3.1)
шекаралық теңдеу
(3.2)
сызықты
дифференциалды есебі берілсін .
облысын
торымен жауып (3.1)-(3.2) есебіндегі
операторларды айырымдық операторлармен
жуықтасақ, онда
(3.3)
(3.4)
есебін
аламыз. Ал
функциялары
тан
тәуелді болғандықтан
ты
өзгерту арқылы, шешулері
параметріне тәуелді (3.3)- (3.4) айырымдық
есептер аламыз. Осы айырымдық есептер
жиынын айырымдық
схема
деп атаймыз.
Жай дифференциалдық теңдеудің Коши есебі:
Айталық,
(3.1)
есебі
берілсін. Бұл есепті шешу үшін
торын алайық та осы торда (3.1) есебін
шешу үшін мынандай айырымдық есеп
қоялық.
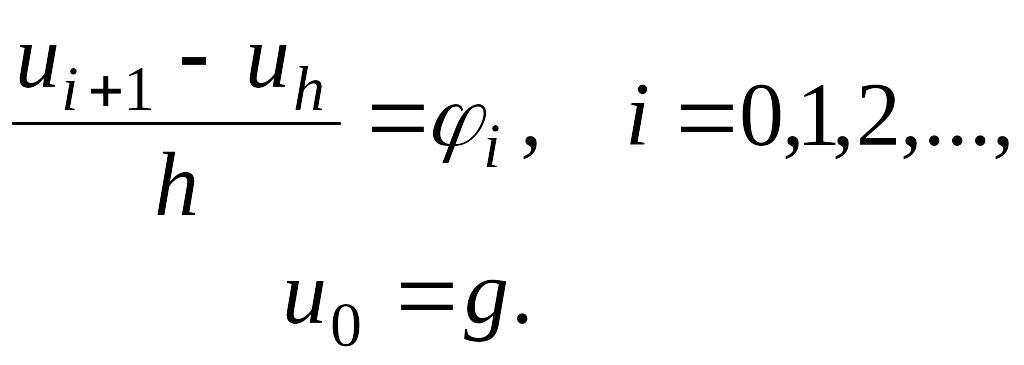
Мұндағы
болуы мүмкін .
Есептің жуық шешуі мына рекурентті формула арқылы табылады.
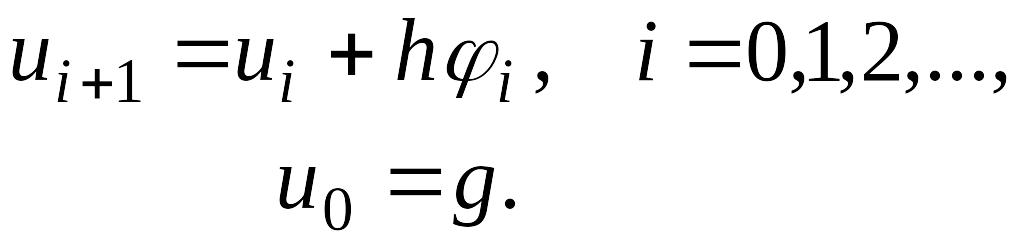
2. Бір ретті дифференциалды теңдеулер жүйесіне қойылған Коши есебі:
Есепті былайша қоямыз.
(3.2)
Мұнда
квадрат
матрица.
өлшемі
ге
тең вектор. Бұл есепті шешу үшін
торында
айырымдық
схеманы пайдаланамыз, яғни
Шекаралық есеп. (Дирихле есебі)
Есеп былайша қойылсын:
(3.3)
Есептің
жуық шешуін табу үшін
кесіндісін
торымен
жабамыз да
үш диагональді алгебралық теңдеулер жүйесімен айырбастаймыз.
Бұл теңдеулер жүйесі қуалау әдісімен шешіледі.
4. Жылу өткізгіштіктің теңдеуіне қойылған бірінші шекаралық есеп.
Бұл есеп былайша қойылады:
(3.4)
облысын
торымен жапсақ, онда (3.4) есебін мына
(3.5)
айырымдық есебімен жуықтауға болады. Мұндағы
т.с.
болуы мүмкін. (3.5) айырымдық схемасын
“анықталған
”
деп атайды, себебі
-ші
қабатта табылған
мәндері
арқылы анықталады, яғни вектор түрінде
жазсақ:
Ал анықталмаған схема былайша жазылады.
,
немесе
Біздің қарастырған мысалдарымызда шекаралық шарттар дәл алынды. Ал есепке екінші және үшінші шекаралық шарттар қойылса, онда оны жуықтау күрделі мәселе болғандықтан кейінге қалдырамыз.
5. Жылу өткішгіштік теңдеуіне қойылған аралас шекаралық есеп
Айталық,
облысында
(3.6)
жылу өткішгіштіктің теңдеуі және
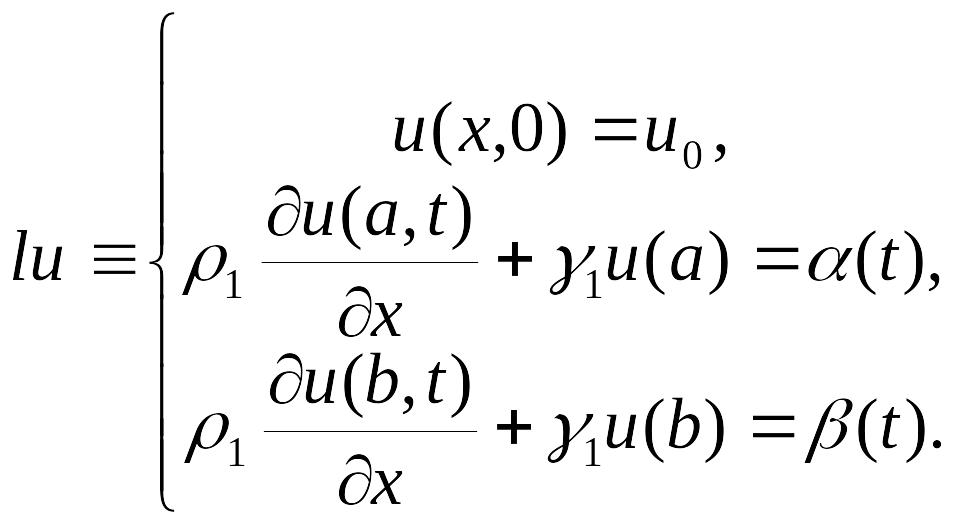(3.7)
шекаралық
шарты берілсін. Мұндағы
белгілі функциялар мен параметрлер.
облысын
торымен
жабайық та есептің бірнеше айырымдық
схемасын қарастырайық.
1
Айқындалған
схема;
қолданылған шаблон
(3.8)
(жуықтау
дәлдігі-
);
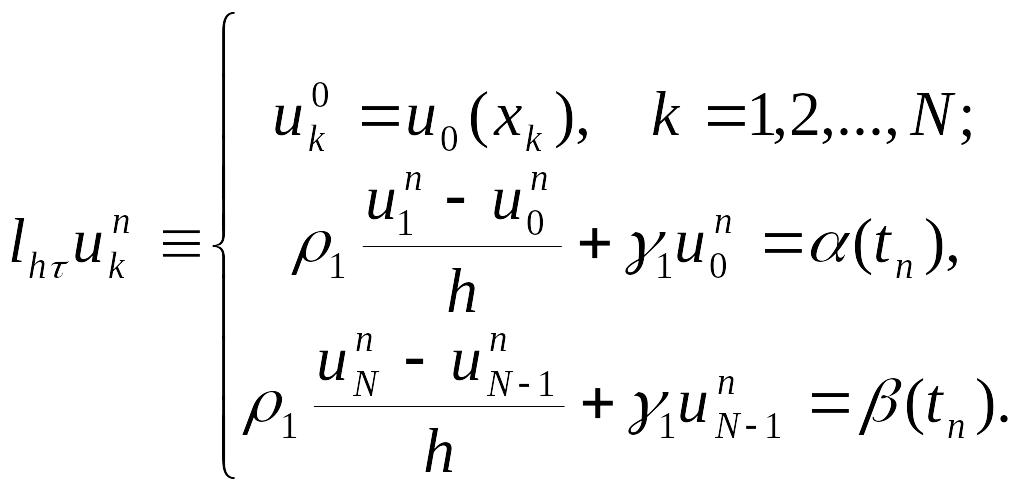(3.9)
(жуықтау
дәлдігі-
).
Схеманың
жалпы дәлдігі-
.
2.
Айқындалмаған схема;
қолданылған шаблон
(3.10)
(жуықтау дәлдігі- );
(3.11)
(жуықтау дәлдігі- ).
Схеманың жалпы дәлдігі- .
3
Крайк-Никольсон
схемасы;
қолданылған шаблон
(3.12)
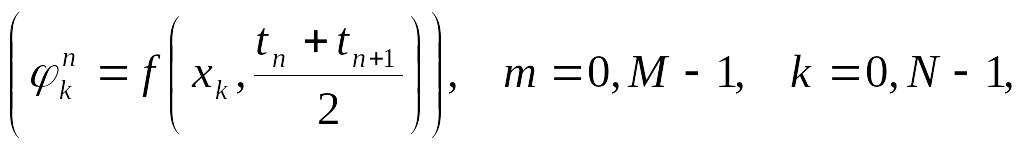
(жуықтау
дәлдігі-
).
(3.13)
(жуықтау дәлдігі- ).
Схеманың
жалпы дәлдігі-
.
Егер
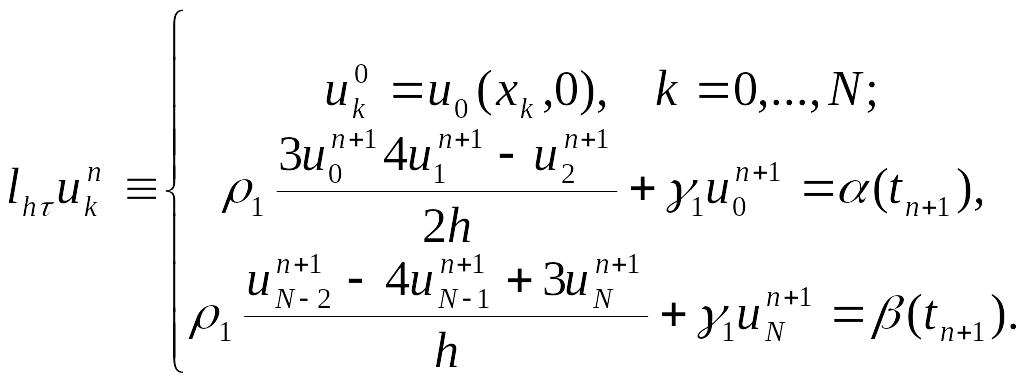(3.14)
(жуықтау
дәлдігі-
).
Айырымымен
жуықтасақ, онда (3.12),(3.14) схемалары (3.6),
(3.7) есебін
дәлдікпен жуықтайды.
Лекция 28-30 4. Айырымдық есептің шешуінің жинақталуы