26. Понятие моделирования. Математическое моделирование.

Моделирование – метод познания, состоящий в создании и исследовании модели.

Модель – некий новый объект, который отражает существенные особенности изучаемого объекта, явления или процесса.

• Предметные (материальные модели) – воспроизводят геометрические, физические и др. свойства объекта в материальной форме.

• Информационные – объекты в образной и знаковой форме

• Образные - зрительные образы объектов, зафиксированные на каком-либо носителе информации

• Знаковые –строятся с использованием различных языков (знаковых систем)

Математическая модель — это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики.

Основные типы задач при математическом моделировании:

1. Решение линейных, алгебраических, трансцендентных уравнений и систем уравнений

2. Решение дифференциальных уравнений и систем

3. Аппроксимация ( приближение функции) - интерполирование, средне квадратическое приближение и др.

4. Решение задач оптимизации

• Решение задач линейного и нелинейного программирования и др.

• Задача планирования эксперимента и т.д.

27. Метод деление отрезков пополам для решения уравнений вида f(x)=0

В интервале [a;b], содержащем один простой корень ( на концах интервала функция имеет разные знаки). Поделим его пополам x=(a+b)/2 [a;x] [x;b] . Выбираем тот на концах которого функция имеет разные знаки, далее цикл до требуемой точности (длинна интервала < ε)

Алгоритм:

Def FNF(x) = ….

Input a,b,eps

2_x = (a+b)/2

If FNF(a)*FNF(x)<0 then b=x else a=x

If b-a >eps then 2

Print x,FNF(x)

End

28. Метод Ньютона для решения нелинейных уравнений вида f(x)=0

При известном хорошем приближении.

Строим последовательность 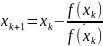сходящуюся к точности

Условия сходимости:

Если точка определена и дважды дифференцируема, причём f(a)*f(b)<0 и f `(x), f ``(x) сохраняется на интервале [a;b]. f(x<sub>0</sub>)*f ``(x₀)>=0.

f(b)>0

f ``(b)>0

Алгоритм

Def FNF (x) = …

Def FNP (x) = …

Input x,eps

2_y = x – FNF(x)/FNP(x)

if ABS (y-x)<ε then 3

x = y : GOTO 2

3_Print y,FNF(y)

End

29. Метод простой итерации для решения уравнений вида f(x)=0

Замена исходного уравненияf(x)=0 на эквивалентноеx = ξ(x) и построение последовательностиx_k+1=ξ(x_k), сходящуюся к точному значению.

Замену можно выполнить разными способами, но самый распространённый

f (x)=0 x=x+

Достаточное условие сходимости:

Функция ξ(x) определена и дифференцируема на интервале [a;b] причём все её значения принадлежат этому интервалу, тогда существует такое число q что <=q<1 то последовательность x_k+1=φ(x_k)k = 0,1,2,3 …. сводится к единственному на [a;b] корню уравнения.

Для оценки точности можно

1. c – искомый корень

2. 

Алгоритм

Def FNF (x) = …

Def FNP (x) = …

Input x,eps

2_y = x – FNF(x)/N

if ABS (y-x)<ε then 3

x = y : GOTO 2

3_Print y,FNF(y)

End

30. Прямые методы решения СЛАУ ( систем линейных алгебраических уравнений). Метод прогонки.

Решение СЛАУ – одно из самых распространённых задач.

Для решения существуют: формула Крамера (через определитель), метод Гаусса, метод прогонки.

Метод прогонки.

При решении систем с матрицами, содержащие много нулевых элементов. В матрицах коэффициентов ненулевые элементы только главные диагонали. Метод прогонки – частный случай метода Гаусса. Метод состоит из прямого и обратного хода. Прямой ход – приведение системы к виду x_i=u_ix_i+v_i ,u_i,v_i – прогоночные коэффициенты, их нахождение – цель прямого хода, для это (i-1) – ое уравнение x_i-1=u_i-1x_i+v_i-1 a_ix_i-1+b_ix_i+c_ix_i+1=d_i

i-ое x_i=

u_i=

v_i=

Обратный ход: при n=ix_n=v_n ,т.к. u_n=0

x_i= u_ix_i+1+v_i i=n;n-1…1

 Прямой ход метода прогонки (вычисление вспомогательных величин):

2 = -c1 / d1 2 = b1 / d1 i+1 = -ci / [di + cii], i=2, ..., n-1 i+1 = [-cii + bi] / [di + cii], i=2, ..., n-1

 Обратный ход метода прогонки (нахождение решения):

xn = [-cnn + bn] / [dn + cnn] xi = i+1xi+1 + i+1, i = n-1, ..., 1

Алгоритм метода прогонки:

1. Ввести коэффициенты системы

2. Выполнить прямой ход

3. Выполнить обратный ход

4. Вычислить невязки r_i=a_ix_i-1+b_ix_i+c_ix_i+1-d_i

5. Вывести результаты x_i,r_i

Достаточное условие устойчивости:

Матрица удовлетворяет условию диагоналей приближений (коэффициенты диагонали больше чем сумма остальной строки)

31. Итерационные методы решения СЛАУ.

Итерационный процесс - последовательное приближение и проверка условия достижения искомого результата.

Позволяют получить решение с любой заданной точностью и не накапливают погрешность округления.

Метод Якоби:

-

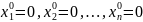
Итерация сходится к точному решению

Достаточное условие сходимости: +

Метод Зейгеля:

-

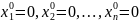
Условие остановки итерационного процесса при требуемой точности ε:

32. Аппроксимация функции. Постановка задачи и способы её решения.

Аппроксимация, или приближение — замена одних объектов другими, в том или ином смысле близкими к исходным, но более простыми.

Задачи:

1. Интерполирование. Близость функции обеспечивается совпадением их значений в узлах интерполяции ( из таблицы, задающей аппроксимируемую функцию). В качестве функции часто выбирают многочлен n-й степени. По Веерштрассу любую гладкую функцию с любой точностью может определить многочлен n-й степени.

2. Среднее квадратичное приближение.В ряде случаев целесообразно приближать функции не по точкам, а в среднем, например, когда необходимо иметь аналитическую зависимость для широкого диапазона значений аргумента, а не только в окрестности некоторого узла, или когда значения функции в узлах определены неточно.

Пусть имеется множество функций , принадлжащих линейному пространству функций. Под близостью в среднем интерполируемой и интерполирующей функций будем понимать результат оценки интеграла