Топологии нейронных сетей.
Полносвязные нейронных сети
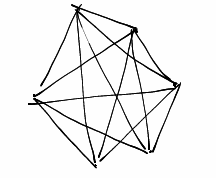
Все нейроны связаны друг с другом. Входные сигналы подаются каждому нейрону. Каждый нейрон передает свой выходной сигнал на все остальные и себе тоже. Выходом сети могут быть все или несколько выходных сигналов после нескольких тактов функционирования сети.
Многослойная сеть
Состоят из нескольких слоев: входной и выходной, и несколько скрытых слоев. Количество нейронов на каждом слое не зависит от количества нейронов на других слоях. Различают многослойные сети прямого распространения и сети с обратными связями, когда выход q+1 скрытого слоя передается на вход предыдущего q слоя.
Слабосвязанные сети
Каждый нейрон связан с 4мя соседним, либо 8
Алгоритмы обучения. Методы Хебба.
Различают алгоритмы обучения с учителем и без учителя.
Алгоритмы обучения с учителем
Такой алгоритм, при котором известны входные и выходные векторы, то есть известны условия задачи и решение. В процессе обучения изменяются параметры сети так, чтобы на выходе получилось результаты, которые нам уже известны. При обучении с учителем задаются множества пар векторов {X,Y}, которое называется обучающим множеством.
{X} = {x1, x2, …, xN} – множество образов
{Y} = {y1, y2, …, yN} – множество допустимых результатов
N – количество элементов в образе.
При обучении изменяются параметры сети таким образом, что сеть научится правильно отображать множество X на множество Y. Количество элементов в обучающем множестве строго не регламентировано, но должно быть достаточным для обучения сети.
Обучение без учителя
Процесс обучения заключается в подстраивании весовых коэффициентах, в некоторых сетях в процессе обучения изменяется и структура нейросети и количество нейронов (сети с
самоорганизацией). Изменения весов могут производиться только на основании информации о состоянии нейронов и уже известных весов. На этом алгоритме по аналогии с принципом самоорганизации нейронов в живых системах построены методы Хебба.
Метод Хебба
Хебб заметил, что синоптическое соединение двух нейронов усиливается, если оба нейрона возбуждены. Для изменения веса он предложил следующую формулу:
Wij(t+1)=Wij(t)+yi[n-1] * yj[n]
Si – уравнение возбуждения i-ого нейрона;
Sj – уравнение возбуждения j-ого нейрона;
Wij(t) и Wij(t+1) весовой коэффициент синапса, соединяющего эти нейроны, на итерациях t и t+1 соответственно;
Этот метод позволяет ответить на сложный вопрос: "Как происходит обучение без учителя?". В методе Хебба обучение является локальным действием, охватывающим только два нейрона. Здесь не нужна система обратных связей.
Сигнальный метод Хебба
В данном методе изменение веса проводится по следующей формуле:
Wij(t+1)=Wij(t)+a *yi[n-1] * yj[n]
yi[n-1] выходное значение нейрона i слоя n-1;
yj[n] выходное значение нейрона j слоя n;
Wij(t) и Wij(t+1) весовой коэффициент синапса, соединяющего эти нейроны, на итерациях t и t+1 соответственно;
a - коэффициент скорости обучения.
При обучении без учителя выполняются следующие шаги:
1) начальные значения весов инициализируются некоторыми небольшими случайными значениями;
2) на входы сети подается входной образ и сигнал о возбуждении распространяется по всем слоям, при этом для каждого нейрона рассчитывается сумма его входов и к полученной сумме применяется функция активации, получаем выходное значение
3) на основании полученных выходных значений по формулам вычисляются новые значения весовых коэффициентов
4) переходим к шагу 2 до тех пор, пока выходные значения не стабилизуются с заданной точностью. На шаге 2 попеременно показываем все входные значения.