
- •26.Зв'язок між моделями Мілі та Мура. Перехід від автомата Мура до автомата Мілі, та навпаки.
- •27.Мінімізація числа внутрішніх станів повністю визначених автоматів.
- •Класифікація тригерів
- •Елементи памяті. Тригери. Rs-тригери. Jk-тригери.
- •Класифікація тригерів
- •Кодування внутрішніх станів цифрових автоматів. Гонки в автоматах. Методи усунення гонок в автоматах.
- •Сусіднє кодування станів цифрових автоматів. Використання шаблонів.
- •Способи опису алгоритмів та мікропрограм.
Сусіднє кодування станів цифрових автоматів. Використання шаблонів.
При
сусідньому кодуванні будь-які два
суміжних стану в графі автомата кодуються
наборами Q 1,...,
Q R, несхожими
станами лише одного елемента (в теорії
кодування такі кодові комбінації
характеризуються мінімальним кодовою
відстанню d =
1). Зазвичай для реалізації сусіднього
кодування граф автомата накладають на
карту Карно відповідного рангу, як це
показано на рис. 4.8 стосовно до графу
рис. 4.5, б.
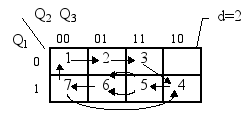 Рис. 4.8. Застосування
сусіднього кодування для станів графа
автомата Мілі рис.4.5, б
4» не зад(перехід
«3 овольняє вимогам сусіднього
кодування)
Сусіднє
кодування, вимоги до якого сформульовані
в роботі [6], не завжди можливо. На рис.
4.9 показані два графа, що не допускають
сусіднього кодування.
Рис. 4.8. Застосування
сусіднього кодування для станів графа
автомата Мілі рис.4.5, б
4» не зад(перехід
«3 овольняє вимогам сусіднього
кодування)
Сусіднє
кодування, вимоги до якого сформульовані
в роботі [6], не завжди можливо. На рис.
4.9 показані два графа, що не допускають
сусіднього кодування.
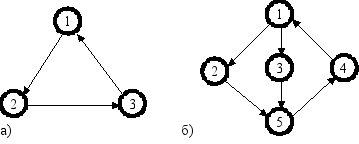 Рис. 4.9 Графи,
що не допускають сусіднє кодування
Рис. 4.9 Графи,
що не допускають сусіднє кодування
Алгоритм кодування станів автомату для D-тригерів. Згідно розглянутого алгоритму при кодуванні необхідно виконати наступне:
Кожному стану автомата а m (m = 1,2, ..., M) ставиться у відповідність ціле число N m, рівне числу переходів у стан а m (N m дорівнює числу появ а m у поле таблиці переходів або числу дуг, що входять в а m при графічному способі завдання автомата).
Числа N 1, N 2,..., N m упорядковуються за спаданням.
Стан а s з найбільшим N s кодується кодом:
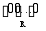 ,
Де R-кількість елементів
пам'яті.
,
Де R-кількість елементів
пам'яті. Наступні R станів згідно списку пункту 2 кодуються кодами, що містять тільки одну 1: 00 ... 01, 00 ... 10, ... , 01 ... 00, 10 ... 00.
Для решти станів знову в порядку списку п.2. використовують коди з двома одиницями, потім із трьома і так далі поки не будуть закодовані всі стани.
У результаті виходить таке кодування, при якому чим більше мається переходів у деякий стан, тим менше одиниць у його коді. Т.к. для D-тригерів функції збудження однозначно визначаються кодом стану переходу, то очевидно, що вирази для функцій збудження будуть простіше. Цей метод особливо ефективний при відсутності мінімізації функцій збудження, що має місце в реальних автоматах з великою кількістю внутрішніх станів і вхідних змінних. Зокрема, для автомата, заданого своїми таблицями переходів і виходів (див. нижче) при кодуванні на базі D-тригерів.
|
a 1 |
a 2 |
a 3 |
a 4 |
a 5 |
|
|
a 1 |
a 2 |
a 3 |
a 4 |
a 5 |
Z 1 |
a 1 |
a 1 |
a 5 |
a 3 |
a 1 |
|
Z 1 |
w 1 |
w 2 |
w 1 |
w 1 |
w 1 |
Z 2 |
a 2 |
a 3 |
a 2 |
a 3 |
a 3 |
|
Z 2 |
w 1 |
w 3 |
w 4 |
w 2 |
w 2 |
Z 3 |
a 3 |
a 4 |
a 2 |
a 4 |
a 2 |
|
Z 3 |
w 2 |
w 2 |
w 2 |
w 1 |
w 3 |
a 1 ~ N 1 = 3 N 3 a 3 = 000 a 2 ~ N 2 = 4 N 2 a 2 = 001 a 3 ~ N 3 = 5 N 1 a 1 = 010 a 4 ~ N 4 = 5 N 4 a 4 = 100 a 5 ~ N 5 = 1 N 5 a 5 = 011 Аналогічно кодуванню внутрішніх станів для D-тригерів можна кодувати вихідні сигнали для будь-якого типу тригерів, тобто чим частіше виробляється даний вихідний сигнал w i, тим менше одиниць у його коді. Так для автомата (рис.41.) Маємо: w 1 ~ N 1 = 6 N 1 w 1 = 00 w 2 ~ N 2 = 5 N 2 w 2 = 01 w 3 ~ N 3 = 2 N 3 w 3 = 10 w 4 ~ N 4 = 2 N 4 w 4 = 11 Передбачається самостійно закінчити синтез автомата при даному кодуванні і при будь-якому іншому. Результати порівняти.
Евристичний алгоритм кодування. Даний алгоритм мінімізує сумарне число переключень елементів пам'яті на всіх переходах автомата і використовується для кодування станів автомата при синтезі на базі T, RS, JK-тригерів. Для даних типів тригерів (на відміну від D-тригерів!) На кожному переході, де тригер змінює своє значення на протилежне, одна з функцій збудження обов'язково дорівнює 1. Зменшення числа переключень тригерів приводить до зменшення кількості одиниць відповідних функцій збудження, що при відсутності мінімізації однозначно приводить до спрощення комбінаційної схеми автомата. Введемо деякі визначення. Нехай Г (S) - неорієнтовані граф переходів автомата S. Вершини графа ототожнюються з станами автомата. Вершини i та j з'єднані ребром, якщо є перехід з а i іа j або навпаки. Позначимо q (i, j) число всіляких переходів автомата з а i в а j. Кожному ребру (i, j) графа Г (S) поставимо у відповідність вага ребра р (i, j) = q (i, j) + q (j, i). Введемо функцію w (i, j) = р (i, j) d (i, j), де d (i, j) - число компонентів, якими коди станів а i в а j відрізняються один від одного (тобто кодова відстань між кодами а i в а j). Функція w (i, j) має простий фізичний зміст. Перходе автомата з а i в а j (або навпаки) супроводжується перемиканням стількох тригерів, скількома компонентами відрізняються коди цих станів, тобто їх число дорівнює w (i, j). Отже, при переході автомата по всіх ребрах, що з'єднує станам а i і а j (їх число p (i, j)!) Всього переключиться кількість тригерів, рівне p (i, j) d (i, j) = w (i , j). Але тоді функція
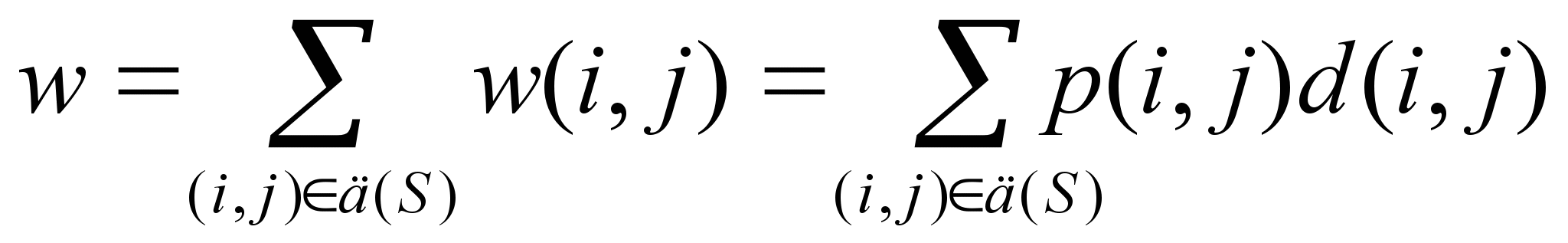 показує,
скільки всього перемикається тригерів
при проходженні автомата по всіх
можливих переходах. Функція w показує,
скільки всього одиниць у функції
збудження, тобто дозволяє оцінювати
складність комбінаційної схеми
автомата. W можна
розглядати як певну цільову функцію,
мінімум якої визначить таке кодування,
при якому комбінаційна схема найбільш
проста. До речі, міінмальное кодова
відстань між різними станами дорівнює
1 і якщо вдається закодувати всі стани
сусіднім кодуванням, то очевидно,
що w буде
мінімально можливим і рівним
показує,
скільки всього перемикається тригерів
при проходженні автомата по всіх
можливих переходах. Функція w показує,
скільки всього одиниць у функції
збудження, тобто дозволяє оцінювати
складність комбінаційної схеми
автомата. W можна
розглядати як певну цільову функцію,
мінімум якої визначить таке кодування,
при якому комбінаційна схема найбільш
проста. До речі, міінмальное кодова
відстань між різними станами дорівнює
1 і якщо вдається закодувати всі стани
сусіднім кодуванням, то очевидно,
що w буде
мінімально можливим і рівним 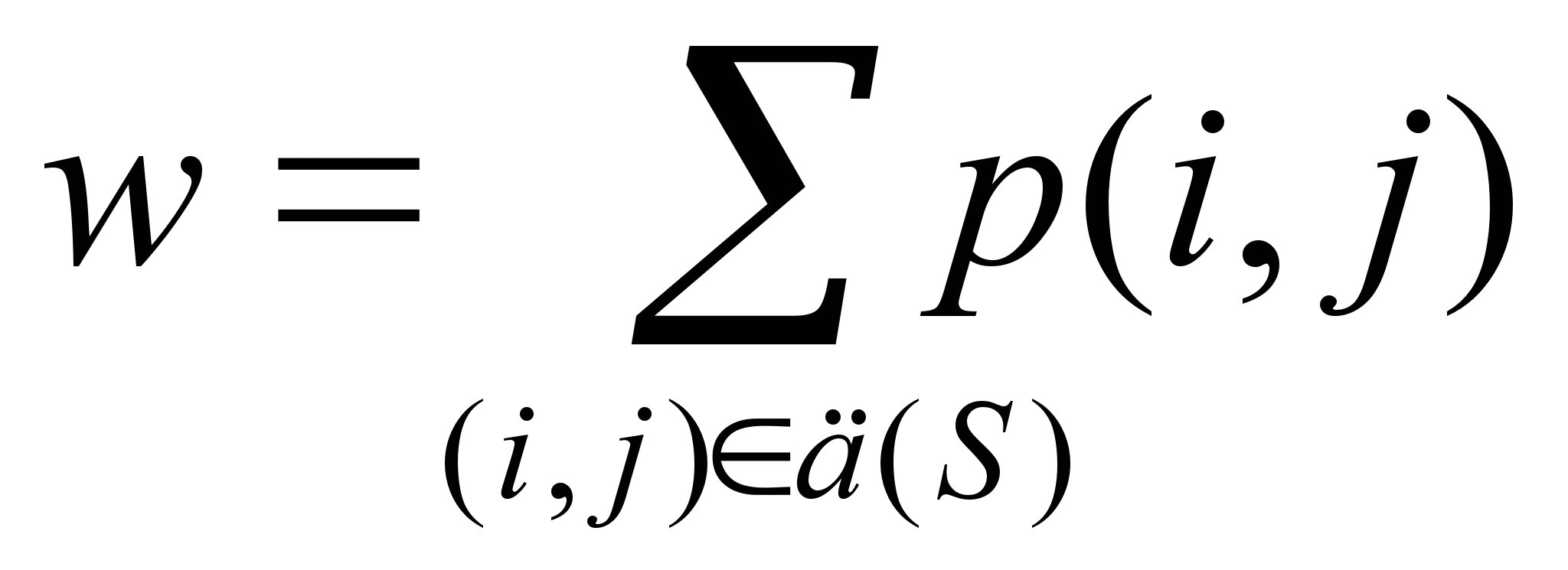 ,
Тобто сумарному числу переходів для
автомата.
З
виразу для w випливає,
що перехід з а i в а i, для
якого d
(i, i) =
0, не впливає на w (що
цілком очевидно, якщо врахувати, що на
цьому переході жоден тригер не
переключається).
Розглянемо
застосування евристичного алгоритму
на конкретному прикладі автомата,
заданого таблицями переходів і виходів
(рис.41.). Для даного автомата можна
побудувати орієнтований граф (без
урахування петель), представлений на
ріс.42. На кожному ребрі вказано його
вагу.
Евристичний
алгоритм складається з наступних
кроків.
1. Будуємо
матрицю
,
Тобто сумарному числу переходів для
автомата.
З
виразу для w випливає,
що перехід з а i в а i, для
якого d
(i, i) =
0, не впливає на w (що
цілком очевидно, якщо врахувати, що на
цьому переході жоден тригер не
переключається).
Розглянемо
застосування евристичного алгоритму
на конкретному прикладі автомата,
заданого таблицями переходів і виходів
(рис.41.). Для даного автомата можна
побудувати орієнтований граф (без
урахування петель), представлений на
ріс.42. На кожному ребрі вказано його
вагу.
Евристичний
алгоритм складається з наступних
кроків.
1. Будуємо
матрицю 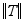 ,
Що складається з усіх пар номерів (i,
j), для
яких р
(i, j)
0 (тобто в автоматі є перехід з а i в а j або
навпаки) і i
<j. Для
кожної пари в матриці
вказуємо
її вагу р
(i, j), що
співпадає з вагою ребра з'єднує а i і а j.
,
Що складається з усіх пар номерів (i,
j), для
яких р
(i, j)
0 (тобто в автоматі є перехід з а i в а j або
навпаки) і i
<j. Для
кожної пари в матриці
вказуємо
її вагу р
(i, j), що
співпадає з вагою ребра з'єднує а i і а j.
|
|
i |
j |
p (i, j) |
|
|
1 |
2 |
2 |
|
|
1 |
3 |
1 |
T |
= |
1 |
5 |
1 |
|
|
2 |
3 |
3 |
|
|
2 |
4 |
1 |
|
|
2 |
5 |
1 |
|
|
3 |
4 |
2 |
|
|
3 |
5 |
2 |
2. Впорядкуємо
рядка матриці
,
Для чого побудуємо матрицю ![]() таким
чином. У перший рядок матриці
помістимо
пару ),
( з
найбільшою вагою ).,
р
( У
нашому випадку ),
( =
(2,3), р (2,3)
= 3. З усіх пар, що мають загальний компонент
з парою ),
( вибирається
пара ),
( з
найбільшою вагою і заноситься у другий
рядок матриці
.
Ясно, що },
{ },
{
0. Потім з усіх пар, що мають загальний
компонент хоча б з однією з внесених
вже в матрицю
пар
вибирається пара з найбільшою вагою і
заноситься в матрицю
і
т.д.. У разі рівності ваг пар обчислюються
суми ваг компонентів пар (вагою )р
( компонента
в матриціназивається
число появ
)
І в матрицю
заноситься
пара з найбільшою сумою ваг. У розглянутому
автоматі на друге місце слідом за парою
(2,3) претендують пари: (1,2) с р (1,2)
= 2; (3,4) с р (3,4)
= 2, (3, 5) з р (3,5)
= 2.
Для
визначення того, яка пара займе друге
місце в матриці
знаходимо
ваги компонентів пар:
р (1)
= 3 р (2)
= 3 р (1)
+ р (2)
= 6
р (3)
= 4 р (4)
= 2 р (3)
+ р (4)
= 6
р (3)
= 4 р (5)
= 2 р (3)
+ р (5)
= 6
У
даному випадку для всіх пар збігаються
і їх ваги і ваги їх компонентів. Тому на
друге місце матриці
може
бути поставлена будь-яка з пар (1,2),
(3,4), (3,5). Але тоді на 3-му і 4-му будуть інші
дві. Виконавши впорядковування всіх
пар, отримаємо матрицю
у
вигляді:
таким
чином. У перший рядок матриці
помістимо
пару ),
( з
найбільшою вагою ).,
р
( У
нашому випадку ),
( =
(2,3), р (2,3)
= 3. З усіх пар, що мають загальний компонент
з парою ),
( вибирається
пара ),
( з
найбільшою вагою і заноситься у другий
рядок матриці
.
Ясно, що },
{ },
{
0. Потім з усіх пар, що мають загальний
компонент хоча б з однією з внесених
вже в матрицю
пар
вибирається пара з найбільшою вагою і
заноситься в матрицю
і
т.д.. У разі рівності ваг пар обчислюються
суми ваг компонентів пар (вагою )р
( компонента
в матриціназивається
число появ
)
І в матрицю
заноситься
пара з найбільшою сумою ваг. У розглянутому
автоматі на друге місце слідом за парою
(2,3) претендують пари: (1,2) с р (1,2)
= 2; (3,4) с р (3,4)
= 2, (3, 5) з р (3,5)
= 2.
Для
визначення того, яка пара займе друге
місце в матриці
знаходимо
ваги компонентів пар:
р (1)
= 3 р (2)
= 3 р (1)
+ р (2)
= 6
р (3)
= 4 р (4)
= 2 р (3)
+ р (4)
= 6
р (3)
= 4 р (5)
= 2 р (3)
+ р (5)
= 6
У
даному випадку для всіх пар збігаються
і їх ваги і ваги їх компонентів. Тому на
друге місце матриці
може
бути поставлена будь-яка з пар (1,2),
(3,4), (3,5). Але тоді на 3-му і 4-му будуть інші
дві. Виконавши впорядковування всіх
пар, отримаємо матрицю
у
вигляді:
|
|
i |
j |
p (i, j) |
|
|
2 |
3 |
3 |
|
|
1 |
2 |
2 |
M |
= |
3 |
4 |
2 |
|
|
3 |
5 |
2 |
|
|
1 |
3 |
1 |
|
|
1 |
5 |
1 |
|
|
2 |
4 |
1 |
|
|
2 |
5 |
1 |
3. Визначаємо
розрядність коду для кодування станів
автомата (кількість елементів пам'яті
- тригерів). Всього станів M = 5. Тоді
R
=] log 2 M
[=] log 2
травня [=
3.
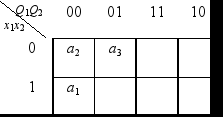
Закодіруем
стану з першого рядка матриці таким
чином: K 2 = K
(а 2) =
000; K 3 = K
(а 3) =
001.
Для
зручності кодування будемо ілюструвати
цей процес картою Карно:

Викреслимо з матриці перший рядок, відповідну закодованим станам а 2 і а 3. Отримаємо матрицю .
|
|
i |
j |
p (i, j) |
|
|
1 |
2 |
2 |
|
|
3 |
4 |
2 |
M ' |
= |
3 |
5 |
2 |
|
|
1 |
3 |
1 |
|
|
1 |
5 |
1 |
|
|
2 |
4 |
1 |
|
|
2 |
5 |
1 |
5. В
силу упорядкування п.2 в першому рядку
закодований рівно один елемент. Виберемо
з першого рядка незакодірованний елемент
і позначимо його . (У
нашому випадку =
1).
6. Будуємо
матрицю ![]() ,
Вибравши з
,
Вибравши з ![]() рядки,
що містять .
рядки,
що містять .
|
|
|
|
i |
j |
p (i, j) |
|
|
|
|
1 |
2 |
2 |
M |
= |
M ' |
= |
1 |
3 |
1 |
|
|
|
|
1 |
5 |
1 |
Нехай B = { 1,..., F} -
безліч елементів з матриці
,
Які вже закодовані. Їх коди До 1,..., K
F відповідно.
У нашому випадку:
B = B 3 =
{2,3} K 2 =
000 K 3 =
001.
7. Для
кожного K
f (f =
1, ..., F) знайдемо ![]() -
Безліч кодів, сусідніх з
-
Безліч кодів, сусідніх з ![]() і
ще не зайнятих для кодування станів
автомата. (Для сусідніх кодів кодова
відстань d = 1).
K 2 =
000
і
ще не зайнятих для кодування станів
автомата. (Для сусідніх кодів кодова
відстань d = 1).
K 2 =
000 ![]() =
{100, 010}
K 3 =
001
=
{100, 010}
K 3 =
001 ![]() =
{011, 101}.
Побудуємо
безліч
=
{011, 101}.
Побудуємо
безліч ![]()
![]() Якщо
виявляється, що
Якщо
виявляється, що ![]() ,
То будуємо нове безліч
,
То будуємо нове безліч ![]() ,
Де
,
Де ![]() -
Безліч кодів, у яких кодова відстань до
коду
дорівнює
2 і т.д..
8. Для
кожного коду з безлічі D знаходимо
кодова відстань до коду
.
K 2 =
000 K 3 =
001
d (100,
000) = 1 d (100,
001) = 2
d (010,
000) = 1 d (010,
001) = 2
d (011,
000) = 2 d (011,
001) = 1
d (101,
000) = 2 d (100,
001) = 1
9. Знаходимо
значення функції w для
кожного коду з безлічі D .
-
Безліч кодів, у яких кодова відстань до
коду
дорівнює
2 і т.д..
8. Для
кожного коду з безлічі D знаходимо
кодова відстань до коду
.
K 2 =
000 K 3 =
001
d (100,
000) = 1 d (100,
001) = 2
d (010,
000) = 1 d (010,
001) = 2
d (011,
000) = 2 d (011,
001) = 1
d (101,
000) = 2 d (100,
001) = 1
9. Знаходимо
значення функції w для
кожного коду з безлічі D .
 10. Із
безлічі D вибираємо
код K , у
якого вийшло мінімальне значення w в
п.9. Вибираємо код для стану a 1 К 1 =
100.
10. Із
безлічі D вибираємо
код K , у
якого вийшло мінімальне значення w в
п.9. Вибираємо код для стану a 1 К 1 =
100.
 11. Із
матриці
викреслюємо
рядки, в яких обидва елементи вже
закодовані, в результаті чого одержимо
нову матрицю
.
Якщо в новій матриці
не
залишилося ні одного рядка, то кодування
закінчено. В іншому випадку повертаємося
до п.5. У нашому випадку маємо:
11. Із
матриці
викреслюємо
рядки, в яких обидва елементи вже
закодовані, в результаті чого одержимо
нову матрицю
.
Якщо в новій матриці
не
залишилося ні одного рядка, то кодування
закінчено. В іншому випадку повертаємося
до п.5. У нашому випадку маємо:
|
|
i |
j |
p (i, j) |
|
|
3 |
4 |
2 |
|
|
3 |
5 |
2 |
M ' |
= |
1 |
5 |
1 |
|
|
2 |
4 |
1 |
|
|
2 |
5 |
1 |
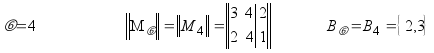 До 2 =
000
=
{010}
K 3 =
001
До 2 =
000
=
{010}
K 3 =
001 ![]() =
{011, 101}
=
{011, 101}
![]() K 2 =
000 K 3 =
001
d (010,
000) = 1 d (010,
001) = 2
d (011,
000) = 2 d (011,
001) = 1
d (101,
000) = 2 d (101,
001) = 1
K 2 =
000 K 3 =
001
d (010,
000) = 1 d (010,
001) = 2
d (011,
000) = 2 d (011,
001) = 1
d (101,
000) = 2 d (101,
001) = 1
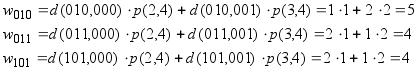 Вибираємо До 4 =
101.
Вибираємо До 4 =
101.

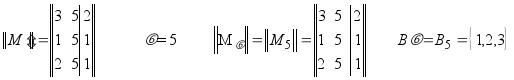 До 1 =
100
До 1 =
100 ![]() =
{110}
K 2 =
000
=
{110}
K 2 =
000 ![]() =
{010}
До 3 =
001
=
{011}
=
{010}
До 3 =
001
=
{011}
![]() До 1 =
100 K 2 =
000 K 3 =
001
d (110,
100) = 1 d (110,
000) = 2 d (110,
001) = 3
d (010,
100) = 2 d (010,
000) = 1 d (010,
001) = 2
d (011,
100) = 3 d (011,
000) = 2 d (011,
001) = 1
До 1 =
100 K 2 =
000 K 3 =
001
d (110,
100) = 1 d (110,
000) = 2 d (110,
001) = 3
d (010,
100) = 2 d (010,
000) = 1 d (010,
001) = 2
d (011,
100) = 3 d (011,
000) = 2 d (011,
001) = 1
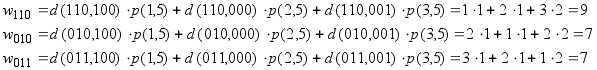 Вибираємо К 5 =
011.
Вибираємо К 5 =
011.
 Т.к.
всі стани автомата закодовані, то робота
алгоритму закінчується. Загальна
кількість перемикань тригерів:
Т.к.
всі стани автомата закодовані, то робота
алгоритму закінчується. Загальна
кількість перемикань тригерів:
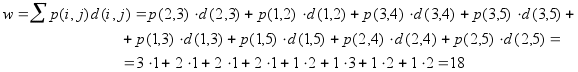 Мінімально
можлива кількість перемикань (якби
стану були закодовані сусіднім
кодуванням)
Мінімально
можлива кількість перемикань (якби
стану були закодовані сусіднім
кодуванням)
![]() Коефіцієнт
ефективності кодування:
Коефіцієнт
ефективності кодування:
![]() Розглянутий
алгоритм кодування є машино-орієнтованим,
існують програми, що реалізують цей
алгоритм.
Необхідно
відзначити в ув'язненні, що використання
алгоритму кодування для D-тригерів або
евристичного алгоритму для інших типів
тригерів забезпечує найбільш просту з
точки зору реалізації схему, але при
цьому можливі гонки. Для радикального
усунення останніх використовують
апаратні методи - тригери з подвійною
пам'яттю: тригери, керовані фронтом і
т.д..
Розглянутий
алгоритм кодування є машино-орієнтованим,
існують програми, що реалізують цей
алгоритм.
Необхідно
відзначити в ув'язненні, що використання
алгоритму кодування для D-тригерів або
евристичного алгоритму для інших типів
тригерів забезпечує найбільш просту з
точки зору реалізації схему, але при
цьому можливі гонки. Для радикального
усунення останніх використовують
апаратні методи - тригери з подвійною
пам'яттю: тригери, керовані фронтом і
т.д..
