Многошаговые игры. Дифференциальные игры.

Пример 10.

Игроки I и II управляют движением точки в евклидовой плоскости, причем каждый сообщает ей свою составляющую скорости, величина которой зависит от положения точки, а направление полностью находится в распоряжении игрока. Скорость точки равна векторной сумме этих составляющих.

Игра заканчивается, когда точка достигнет оси х; выигрыш равен времени, необходимому для завершения игры, плюс величина x₀²/8, где х₀ — абсцисса точки, в которой заканчивается партия.

Если мы обозначим через u = у и w = х + у величины составляющих скорости, которыми управляют соответственно игроки I и II, то получим кинематические уравнения

и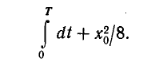 выигрыш

Таким образом, для всех х и у мы имеем К = 1.

Ясно, что если u > w, то игрок I всегда может продолжать игру неограниченно. Поэтому мы будем интересоваться только точками в положительном квадранте.

Основное уравнение для этой игры будет следующим:

Д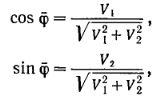 ля того чтобы максимизировать первое слагаемое левой части, мы должны положить

а чтобы минимизировать второе слагаемое – положить

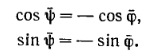
Е сли мы подставим эти значения, то после упрощений получим

К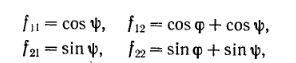 роме того,

и после подстановки в эти выражения мы получим уравнения траекторий

Е сли вместо прямого времени мы введем обратное время τ = Т — t, то мы получим уравнения траекторий в обратном времени

где — производная по τ и т. д.

К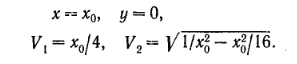 роме того, мы имеем начальные условия, а именно при τ = 0

Из этих условий следует, что мы должны иметь х₀≤2; это условие в свою очередь означает, что никакая траектория не заканчивается в точке х₀>2.

Если мы продифференцируем по τ, то получим

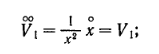
э то уравнение имеет решение

откуда в свою очередь

Положив х_о = а и разрешив начальные условия относительно С₁ и С₂, мы получим

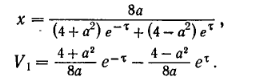
Для того чтобы найти у, заметим, что

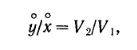
о ткуда, учитывая, что V₂ постоянна вдоль любой оптимальной траектории, получаем

Д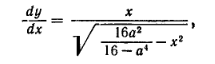 алее, V₂(0) задано, a V₁ можно найти как функцию х; это преобразование дает нам уравнение

которое имеет решение

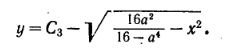
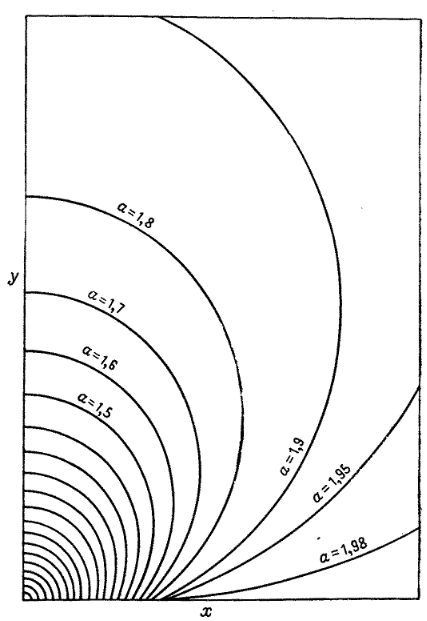
Учитывая, что при у = 0 будет х = а, находим С₃. Таким образом, и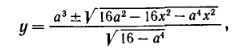 меем

и ли, что эквивалентно,

иначе говоря, оптимальная траектория представляет собой окружность с центром на оси у. Значение V (х, у) можно найти, относительно а, а затем разрешая относительно τ; тогда Можно также найти оптимальные стратегии: оба игрока пытаются следовать касательной к окружности. Игрок I (максимизирующий) толкает вверх (от оси х)\ игрок II толкает вниз (к оси х).

Антагонистические игры

• Антагонистической игрой называется некооперативная игра, в которой участвуют два игрока, выигрыши которых противоположны.

• Формально антагонистическая игра может быть представлена тройкой <X, Y, F>, где X и Y — множества стратегий первого и второго игроков, соответственно; F — функция выигрыша первого игрока, ставящая в соответствие каждой паре стратегий (ситуации) (x,y), 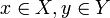  действительное число, соответствующее полезности первого игрока при реализации данной ситуации. Так как интересы игроков противоположны, функция F одновременно представляет и проигрыш второго игрока.

Пример 11.

Игра «Орленок».

• Игрок I выбирает «решко» (Р) или «герб» (Г).

• Игрок II, не зная выбора игрока I, также выбирает «решко» или «герб».

• Если оба противника совершают одинаковый выбор, то игрок II выигрывает единицу у игрока I;

• в противном случае игрок I выигрывает единицу у игрока II.

На дереве игры векторы при окончательных позициях представляют функцию выигрыша; число при каждой из остальных позиций означает игрока, которому принадлежит очередь хода в этой позиции. Затененная область охватывает позиции из одного информационного множества.

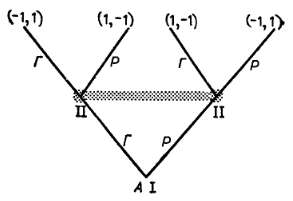
В аналитическом виде функция выигрыша первого игрока имеет следующую форму:

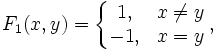
где x ∈ X и y ∈ Y — стратегии первого и второго игроков, соответственно.

Так как выигрыш первого игрока равен проигрышу второго, то  .