Кооперативные игры

Кооперативные игры отличаются от игр другой категории, бескоалиционных игр, тем, что в них возможны так называемые обязывающие соглашения между игроками.

Пример 7.

• Простая мажоритарная игра трех лиц. Это игра трех лиц с нулевой суммой.

• Каждый игрок выбирает один из номеров других игроков, причем ходы всех трех игроков делаются одновременно — делая выбор, игрок не знает, какие выборы сделали другие игроки. Если два игрока выбрали друг друга, то они образовали пару. Будет создана либо 1 пара, либо ни одной. Если пара есть, то оба игрока этой пары получают по 1/2, а третий (исключенный игрок) теряет 1. Если пар нет, то у всех игроков нулевой выигрыш.

• Было бы неразумно не образовывать коалиций, но то, какая именно из трех коалиций будет образована, выходит за рамки теории.

Возможны модификации правил:

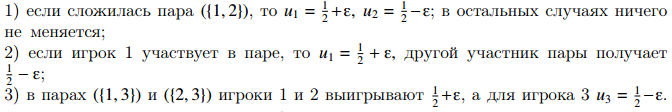
Рассмотрим модификацию 1.

• Хотя игрок 1 по правилам игры имеет преимущество, он не может им воспользоваться. Предположим, что игра не допускает соглашений между игроками. Тогда (при условии рациональности игроков) игрок 1 выберет игрока 2, т.к. для него пара (1,2) более привлекательна;

• Игрок 2 выберет игрока 3, т.к. для него пара (1,2), напротив, непривлекательна;

• Поскольку пара (1,3) никогда не составляется, игрок 3 выберет игрока 2.

• Лучшее, что в сложившейся ситуации может сделать игрок 1, это возвратить добавку ε игроку 2, чтобы сделать пару (1,2) столь же привлекательной для игрока 2, как конкурирующая пара (2,3).

В кооперативных играх с трансферабельной полезностью, то есть возможностью передачи средств от одного игрока к другому, невозможно применять понятие индивидуальных платежей. Вместо этого используют так называемую характеристическую функцию, определяющую выигрыш каждой коалиции игроков. При этом предполагается, что выигрыш пустой коалиции равен нулю.

Пример создания характеристической функции(8).

Игра «Акции».

Все 100% акций компании поделены между n акционерами, i-й акционер владеет w(i) процентами акций, коалиция K совместно владеет процентами акций, тогда v(K) = f(w(K)); где f : [0; 100] → [0; 1] — юридическая сила пакета акций. Например, когда все решается простым большинством, получается простая игра с функцией.

• Пусть акции распределены следующим образом (см. таблицу слева); тогда можно вычислить характеристическую функцию.

Решение кооперативных игр (дележ).

• Игроки обозначаются натуральными числами и множество игроков в игре n лиц имеет вид

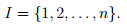
• Любое подмножество множества игроков называется коалицией.

• Функция , ставящая в соответствие каждой коалиции уверенно получаемый ею выигрыш, называется характеристической функцией игры.

• Исход игры можно описать так называемым дележом. Так называется n-мерный вектор 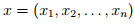, элементы которого удовлетворяют следующим соотношениям:

1. — условие индивидуальной рациональности;

2. 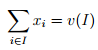— условие коллективной рациональности.

• Первое условие означает, что игрок в результате дележа получает не меньший выигрыш, чем он мог бы получить и так, не договариваясь с другими игроками.

• Второе условие означает, что делится весь возможный суммарный выигрыш. Если сумма элементов дележа меньше этой величины, то объединять усилия бессмысленно. Если больше — значит, в игре появились откуда-то лишние деньги, что нарушает условия.

• Принцип сравнения дележей между собой устанавливает определение доминирования дележей. А именно, говорят, что дележ x доминирует дележ y, если

1. — условие единогласия ;

2. — условие реализуемости.

• Наконец, вводится понятие C-ядра, как один из вариантов понимания оптимального решения в кооперативной игре. C-ядром кооперативной игры называется множество дележей, для которых не существует дележей, их доминирующих.

Пример 9.

Рассмотрим игру 3-х лиц с характеристической функцией следующего вида:

• Найдем C-ядро этой игры. Дележом будет вектор x = (x₁; x₂; x₃) , удовлетворяющий условиям:

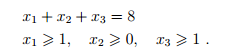
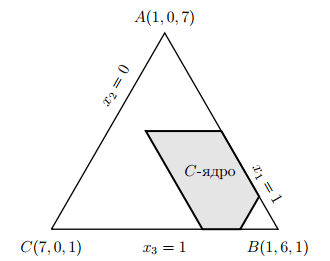
• Первое условие означает, что дележи лежат в одной плоскости, а остальные описывают многоугольник в этой плоскости. Изобразим это на рисунке.

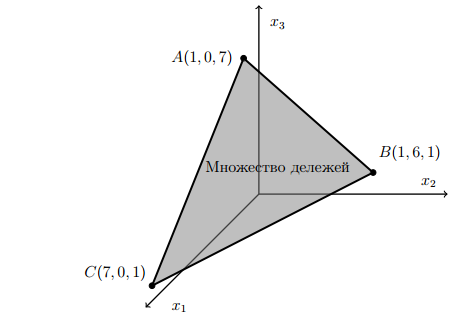
• Как видно из рисунка, вершинами многоугольника являются дележи, в которых поочередно по две компоненты принимают свои наименьшие возможные значения.

• Воспользуемся критерием принадлежности дележа C-ядру, который заключается в выполнении неравенства

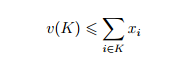
для каждой коалиции K.

В нашем случае это означает, что на компоненты вектора x = (x₁; x₂; x₃) накладываются условия:

Чтобы нарисовать множество, например, x₁ + x₂ 4 или, что то же самое, x₃ ≤ 4, достаточно заметить, что прямая x₃ = 4 будет параллельна стороне BC треугольника и пересекать две другие стороны треугольника на одинаковом расстоянии от вершин B и C. Это расстояние равно 4. А, поскольку координата x₃ убывает по мере приближения к этим вершинам, то множество точек треугольника, для которых x₃ ≤ 4, будет лежать между прямой x₃ = 4 и отрезком BC, как показано на рисунке:

Аналогично можно изобразить и остальные условия. Пересечение полученных многоугольников и будет C-ядром игры. Оно изображено на следующем рисунке.

Нарисуем таблицу, следуя первому способу построения вектора Шепли

Легко проверить, что дележ Шепли принадлежит C-ядру игры:

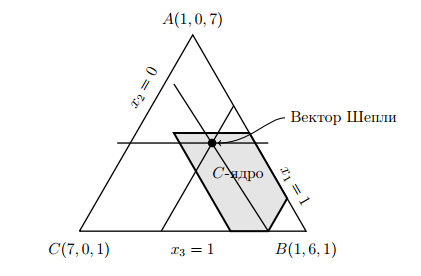
Как видим, в этом случае справедливый дележ является также и устойчивым, то есть, по крайней мере, не существует дележей, его доминирующих.