Вплив переробки для кожної технології

Параметри (рівні фактора, )		Результати часу переробки відходів (значення функції відгуку ), годин				Кількість вимірів	Дослідне середнє,
		Номер виміру
		1	2	3	4
Вид технології переробки		8	11	14	15	4	12
		4	5	9	4	4	7
		3	4	6	4	4	5

Розв’язання. За даними таблиці 3.23, визначаємо середні:

годин;

годин;

годин

і загальну середню годин.

Визначаємо дисперсію

; .

Перевірка: ,

звідси

;

; ; .

,

тобто рівняння виконується.

Знаходимо статистику

.

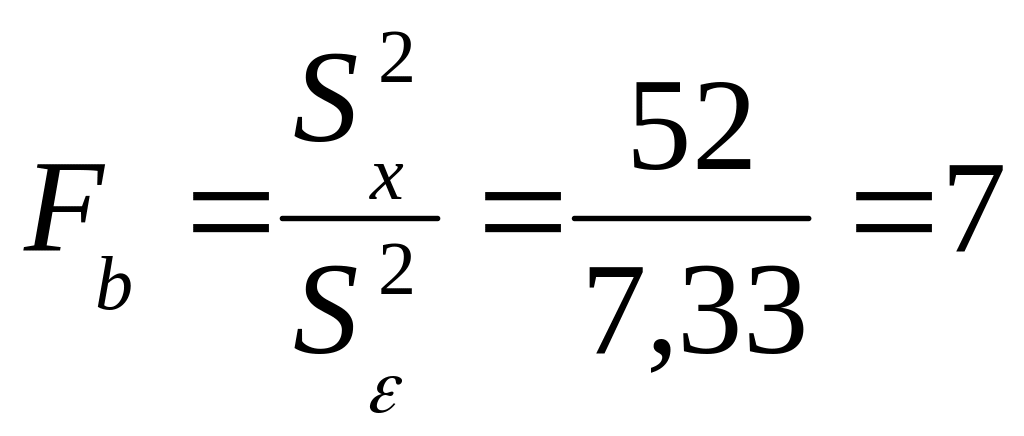При рівні значущості величина (див. додаток 6).

Тоді

> =4,28.

Звідси випливає, що гіпотеза про рівняння середніх відкидається, тобто на тривалості переробки позначається обраний вид технології.

Для визначення ступеня впливу технології на тривалість переробки відходів обчислюємо кореляційне відношення

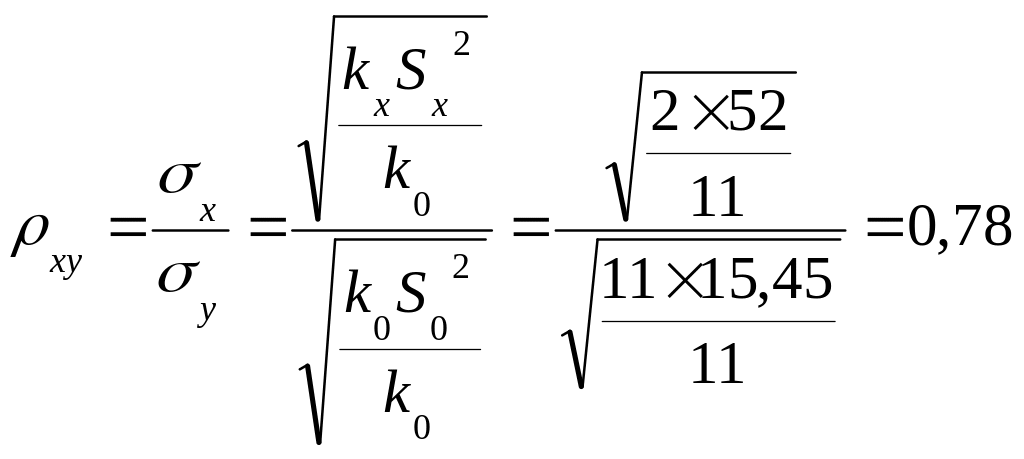
Це означає, що при ознака (вид технології переробки відходів) є домінуючим і 61% розкиду тривалості переробки щодо загального середнього обумовлюється саме цим фактором. Решта 39% припадають на частку неврахованих факторів.

Однофакторний дисперсійний аналіз при нерівночисельних серіях спостережень.

При різній кількості паралельних спостережень на різних рівнях схема проведення і основні прийоми аналізу залишаються колишніми. Змінюються лише деякі висловлювання:

1) загальне число спостережень ;

2) суми спостережень за серіями ;

3) середні в серіях ;

4) загальне середнє ;

5) співвідношення для сум

;

6) співвідношення для числа ступенів свободи

;

7) дисперсія фактору при суттєвому впливі фактору

.

Обчислювальний алгоритм однофакторного дисперсійного аналізу спрощується, якщо для розрахунку сум квадратів відхилень використовувати перетворення

.

Тоді для суми отримуємо зручні розрахункові формули:

;

;

.

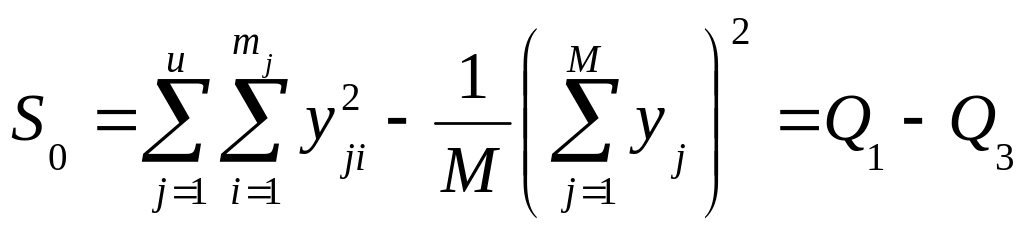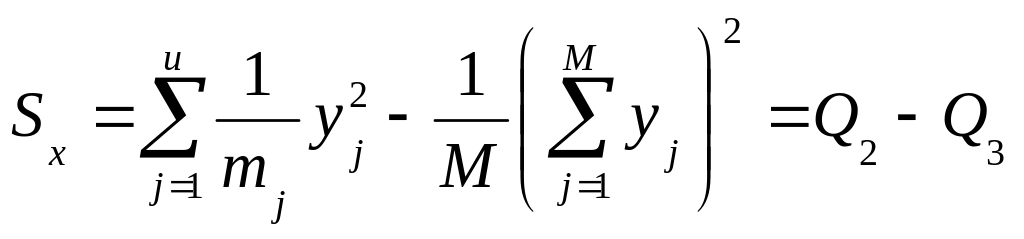Звідси

;

; ; .

Далі

; ; ; .

Приклад. Досліджувалося очищення стічних вод способом осадки твердих частинок на протязі певного терміну відстою. Результати дослідження наведені в таблиці 3.24.

Таблиця 3.24.

Результати дослідження очищення стічних вод

Термін відстоювання стічних вод (фактор ), дні	Величина осаду у г/м3 води (функція відгуку )						Кількість вимірів
	Номер досліду
	1	2	3	4	5	6
15	8,0	8,4	9,0	8,6	-	-	4
20	8,2	9,0	10,0	10,0	9,2	10,0	6
25	11,0	13,0	-	12,0	-	-	3
30	7,5	8,5	-	-	-	-	2

Потрібно визначити вплив тривалості відстоювання на величину осадження твердих частинок.

Розв’язання. За даними табл.3.24 визначаємо:

1) середні

;

;

;

;

2) загальну середню

3) дисперсії

.

;

4) - статистику

.

При рівні значущості визначаємо критичне значення -критерію за таблицею (див. додаток 6, с).

.

Звідси витікає, що гіпотеза про рівняння середніх відхиляється, тобто величина осадки залежить від тривалості відстоювання.

5) кореляційне відношення

де

Отже, при , час відстоювання стічних вод впливає на величину осадження, і на 80% розкиду величини осаду щодо загальної середньої обумовлено саме тривалістю відстоювання.

Двофакторний дисперсійний аналіз.

Нехай вивчається вплив двох одночасно діючих факторів і . Надамо результати експерименту в табл. 3.25. Дослідження складалося з спостережень ,

де - порядковий номер рівня варіювання фактора ( );

- порядковий номер рівня варіювання фактора ( );

- порядковий номер паралельного досліду в серії при кожному поєднанні факторів і ( ).

Для спрощення викладок розглянемо випадок рівночисельних серій спостережень при всіх можливих сполученнях рівнів, тобто .

Обчислимо середнє арифметичне серій з повторних спостережень для кожного поєднання -того і - того рівнів факторів і .

.

Середнє арифметичне по рядках , зі спостережень (див. табл. 3.25) для кожного - того рівня фактору

.

Таблиця 3.25