1 7

Аналіз впливу окремих факторів у екологічній моделі

                  В екології часто зустрічаються об'єкти дослідження, стан яких визначається факторами, що не мають кількісної оцінки. Такими факторами можуть бути некеровані і керовані змінні, які з яких-небудь причин не дозволяють проводити їх вимірювання в даному експерименті, а також не контрольовані змінні, рівні варіювання яких можна довільно вибирати і фіксувати за часом.

Для вивчення впливу факторів подібного роду на функцію відгуку (цільову функцію), їх спільного оцінювання, рангування і виділення серед них істотних методи регресійного аналізу непридатні, оскільки вони вирішують завдання визначення виду математичної моделі при варіюванні величиною факторів. Тут доцільно використовувати методи дисперсійного аналізу.                   Розглянемо постановку задачі дисперсійного аналізу в загальному вигляді. Нехай досліджується певний процес, що описує функції

Величина може залежати (з якихось фізичних причин) від незалежних керованих факторів , що не мають кількісного опису, і їх парних взаємодій.

При цьому:

• кожен фактор може змінюватись на, рівнях;

• повний факторний експеримент складається з 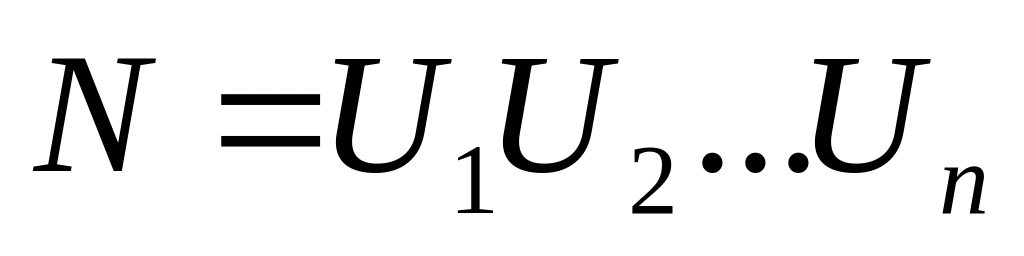серій незалежних спостережень за числом усіх можливих неповторюваних сполучень рівнів - факторів;

• кожна - серія містить спостережень паралельних дослідів.

                  Потрібно визначити, якою мірою на тлі випадкових похибок істотний вплив того чи іншого фактора або взаємодія факторів на відгук ; провести порівняння з іншими факторами і виділити найбільш суттєві.

При дослідженні приймаються наступні припущення:

• спостережувані величини функції відгуку , мають нормальний розподіл з центром 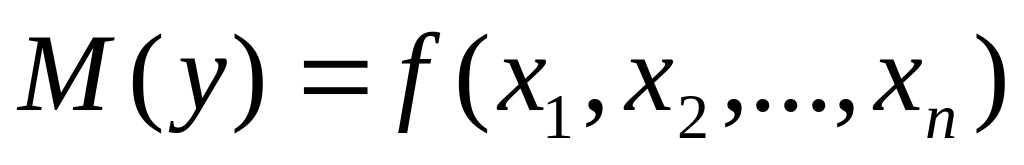. Таким чином, фактори визначають величину лише у середньому, залишаючи простір для випадкових помилок спостережень, що підкоряються нормальному розподілу;

• дисперсія одиничного спостереження 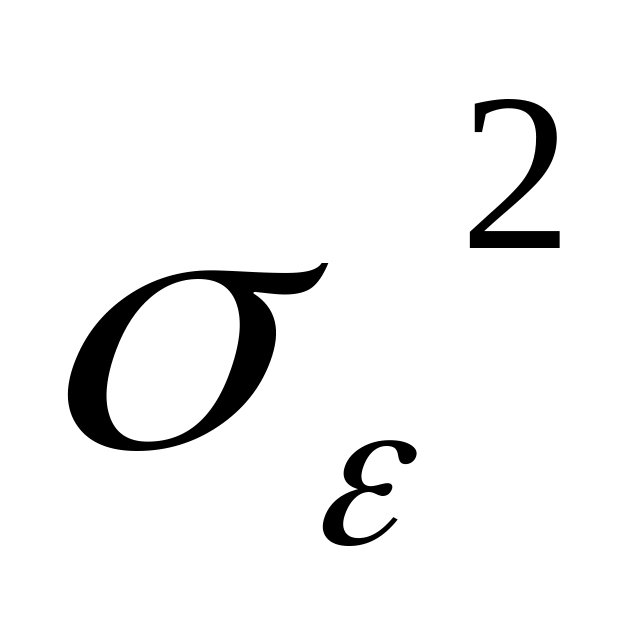, обумовлена випадковими помилками , постійна у всіх дослідах, не залежить від значень , тобто дисперсії і рівні (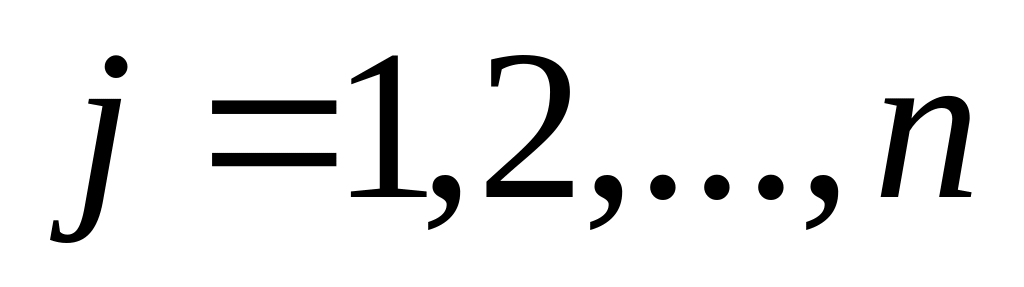 ), а їх вибіркові оцінки 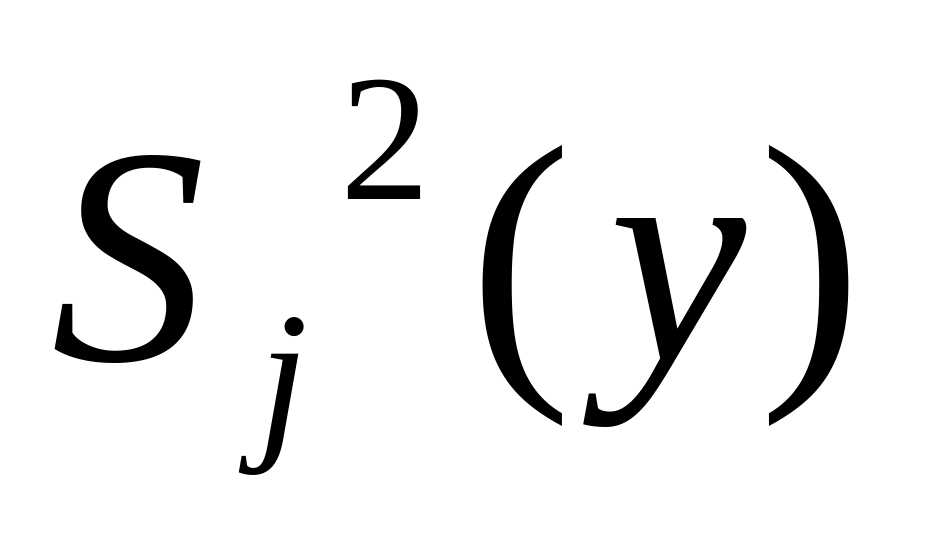однорідні, тобто дотримується умова відтворюваності дослідів з рівною точністю.

                  Кожне з цих припущень необхідно перевіряти в процесі аналізу експерименту.

З даних завдання і припущень очевидно, що чим значніший вплив деякого фактора на функцію відгуку , тим більше розходження між собою середніх арифметичних відгуків в серіях паралельних спостережень, зроблених при різних рівнях варіювання фактора . При двох серіях спостережень порівняння середніх і перевірка гіпотези про не значущості їх відмінностей проводиться за допомогою - критерію Стьюдента.                   У сформульованому завданні потрібно одночасно зіставляти довільно велике число середніх і на підставі цього можна зробити висновок про суттєвість впливу того чи іншого фактора.

Щоб мати можливість оцінювати вплив кожного фактора на функцію відгуку і порівнювати вплив різних факторів, встановимо деякий кількісний показник цього впливу. Нехай за відсутності помилок досліду ( ) при варіюванні факторів на різних рівнях отримані дослідні значення функції відгуку . Тоді як показник впливу фактора приймемо величину, яку за аналогією зі звичайною дисперсією називають дисперсією фактора

,

де . При цьому будемо мати на увазі, що числа не є випадковими і тому дисперсія не пов'язана ні з якою випадковою величиною, бо ми вважаємо, що дисперсія помилок .

                  Вивчити вплив факторів за величинами їх дисперсій зручно, оскільки це найпростіша міра розсіювання і до того ж аналогічна мірі впливу фактора випадкових причин, тобто дисперсії одиничного спостереження (відтворюваності) .

                  Завдяки цьому є можливість порівнювати вплив будь-якого досліджуваного фактора і фактора випадковості. Таке дослідження факторів за їх дисперсіями називають дисперсійним аналізом, який був запропонований Р.Фішером і розвинений Р.Йєйтсом.

Розглянемо ідею дисперсійного аналізу на прикладі вивчення фактора на тлі випадкових похибок, коли дисперсія відтворюваності відома.

При варіюванні фактора на - рівнях в результаті спостереження (без проведення паралельних дослідів на кожному - тому рівні) отримаємо значення функції відгуку , розсіювання яких можна оцінювати дисперсією

з числом ступенів свободи . Якщо відмінність від незначна, то розкид спостережень, який вона характеризує, пов'язаний лише з випадковими причинами і вплив фактора неістотний. Якщо ж відмінність від значна, то підвищений розкид спостережень викликається не тільки випадковими причинами, але ще і впливом фактора , яке тепер потрібно визнати істотним.

Оскільки в останньому випадку впливи двох незалежних факторів об’єднуються , то це може бути:

• від випадкових причин з дисперсією ;

• від фактора з дисперсією , що призводить до загального розсіювання спостережень. У результаті загальна дисперсія є сумою, що складається з двох дисперсій

.

У загальному випадку, коли дисперсія відтворюваності невідома, схема дисперсійного аналізу повинна дозволити провести її оцінку поряд з оцінками дисперсій досліджуваних факторів.

                   Таким чином, основна ідея дисперсійного аналізу полягає в розкладанні оцінки загального розсіювання функції відгуку на складові, які залежать:

• від випадкових причин;

• від кожного з розглянутих факторів;

• від взаємодії факторів;

• від оцінки статистичної значущості дисперсій факторів з

урахуванням помилки відтворюваності досліду.

Техніка дисперсійного аналізу досить різноманітна. Ми розглядаємо лише найпростіші способи, що найбільш часто зустрічаються в практиці.                   Однорідний дисперсійний аналіз. Розглянемо методику вивчення впливу одного фактора на цільову функцію. Представимо результати експериментів (всього спостережень ) у вигляді табл.3.22.

Таблиця 3.22