3.7.3. Опори приймача сполучені трикутником

3 .7.3.1. Симетричне навантаження фаз

Для спрощення розрахунків перетворимо трикутник опорів приймача в еквівалентну зірку опорів .

Комплексний опір променя симетричної зірки:

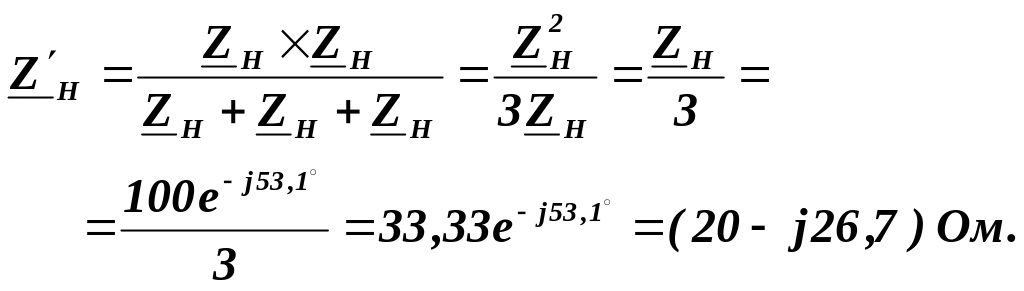
Надалі порядок розрахунку перетвореної схеми такий же, як і схеми зірки без нульового проводу при симетричному навантаженні (завдання 3.7.1.1).

Отже, комплексні провідності симетричного навантаження фаз генератора:

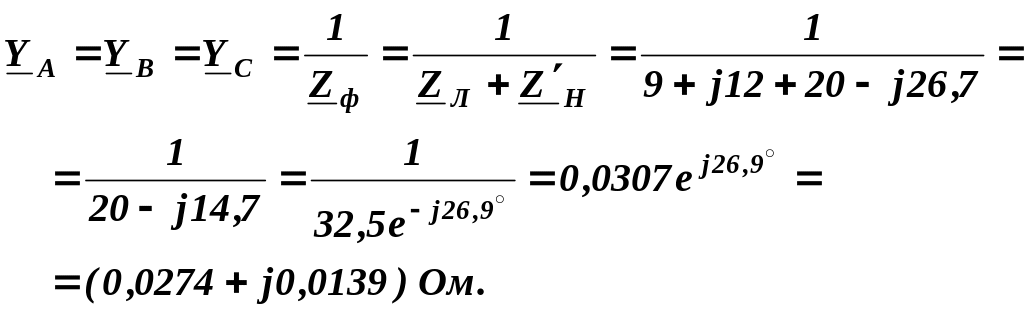Комплексні лінійні струми:

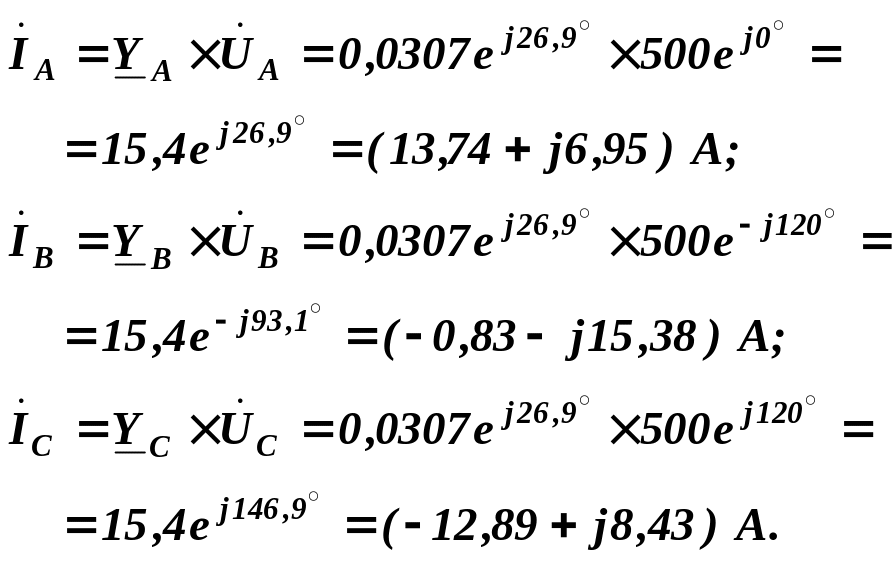
Перевірку правильності обчислень комплексних струмів виконаємо, записавши рівняння першого закону Кірхгофа для перерізу :

Так як комплексні фазні струми еквівалентної зірки приймача рівні комплексним лінійним струмам генератора, то комплексні фазні напруги еквівалентної зірки приймача:

Комплексні лінійні напруги приймача:

Так як відповідні комплексні лінійні напруги початкової і перетвореної схеми приймача одні й ті ж, то комплексні фазні струми трикутника приймача визначаються із відношень:

Перевірку правильності обчислень комплексних фазних струмів зробимо, склавши рівняння першого закону Кірхгофа для вузла :

Комплексна потужність симетричного трифазного приймача:

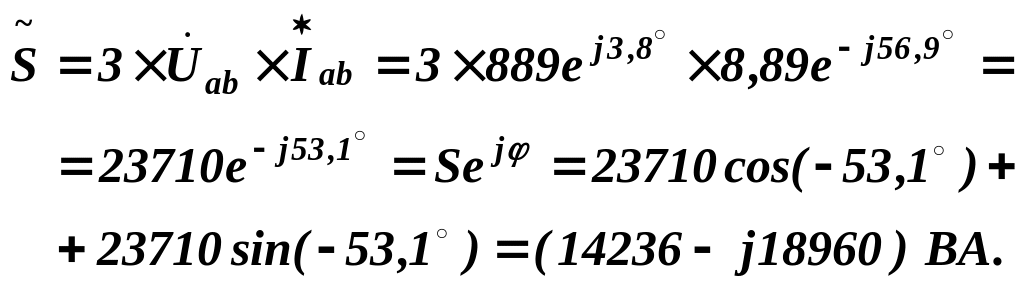
Отже, трифазний симетричний приймач споживає:

активну потужність ; реактивну ємнісну потужність .

Повна (установлена) потужність приймача

Комплексні спади напруг на опорах лінійних проводів:

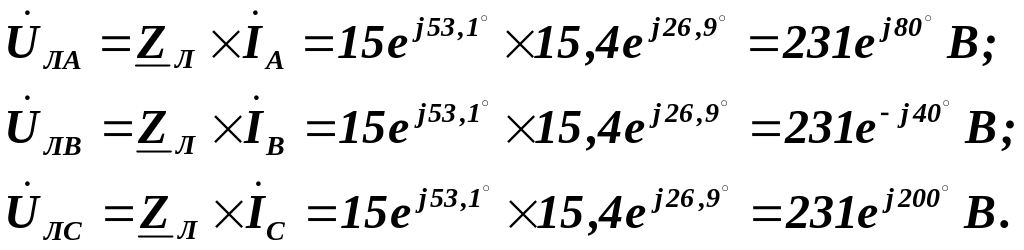
Використовуючи обчислені значення комплексних напруг і струмів, будуємо на комплексній площині топографічну векторну діаграму (рис. 3.24).

Вектори фазних і лінійних напруг генератора відкладаємо на комплексній площині звичайним способом (завдання 3.7.1.1).

Вектори фазних напруг , й еквівалентної зірки приймача відкладаємо з вузлової точки „ ”.

Вектори лінійних напруг приймача , й відкладаємо у відповідності з векторними рівностями:

Вектори спадів напруг на опорах лінійних проводів являють собою векторні різниці фазних напруг генератора і відповідних фазних напруг приймача:

Вектори фазних струмів , й трикутника приймача відкладаємо з вузлової точки « », а вектори лінійних струмів приймача відкладаємо у відповідності з векторними рівняннями:

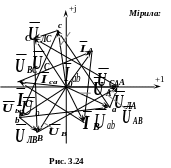
3.7.3.2. Обрив лінійного проводу

Для спрощення розрахунків перетворимо трикутник опорів приймача в еквівалентну зірку опорів , комплексний опір променя якої (завдання 3.7.3.1):

Так як провід обірваний, то опір його , а провідність:

З попереднього розрахунку:

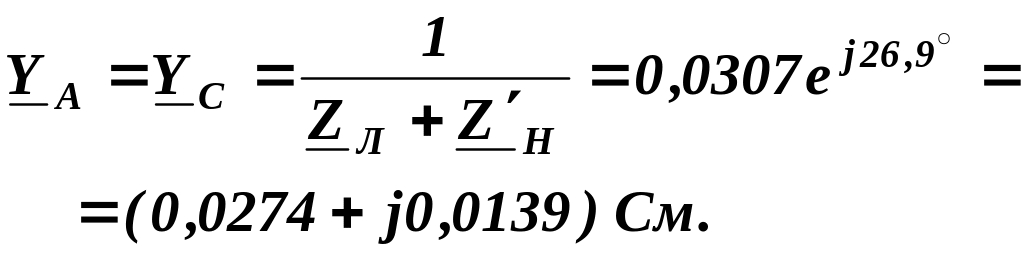Комплексна напруга зміщення нейтралі:

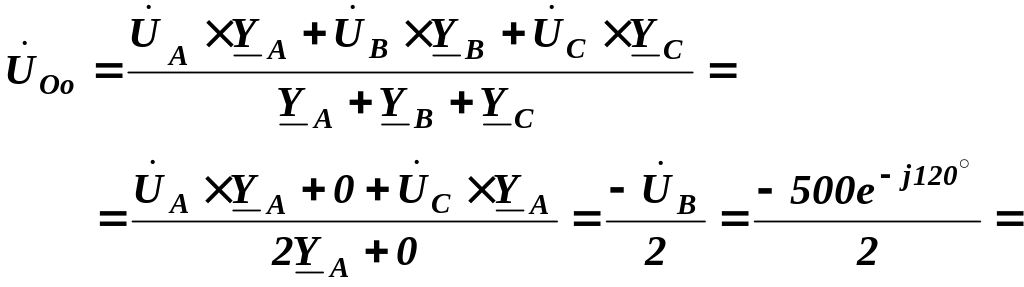
Комплексні лінійні струми:

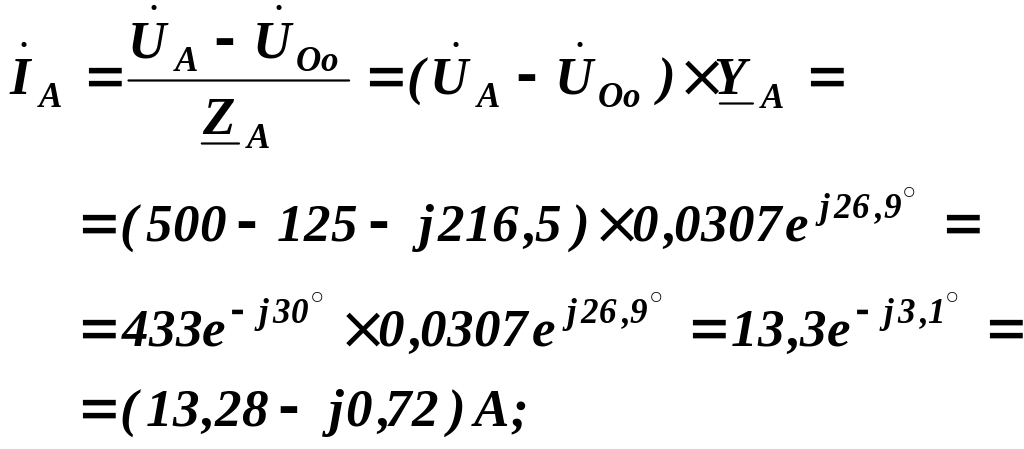
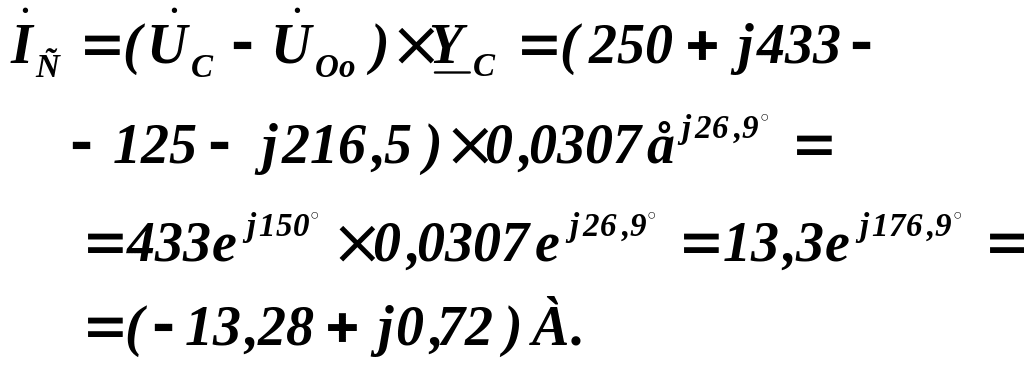
Комплексні спади напруг на опорах лінійних проводів:

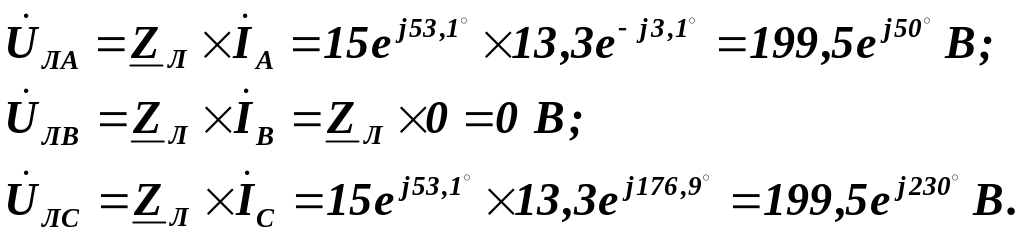
Комплексні фазні напруги еквівалентної зірки опорів приймача:

Комплексні лінійні фазні напруги трикутника опорів приймача:

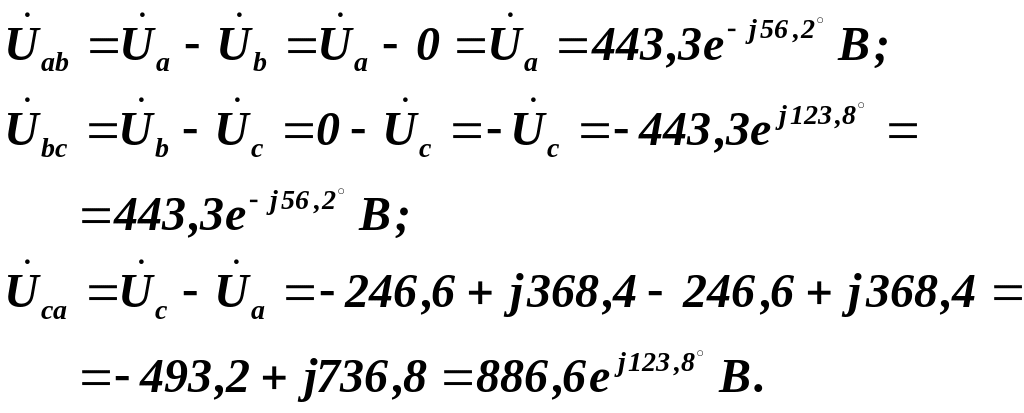
Комплексні фазні струми трикутника приймача:

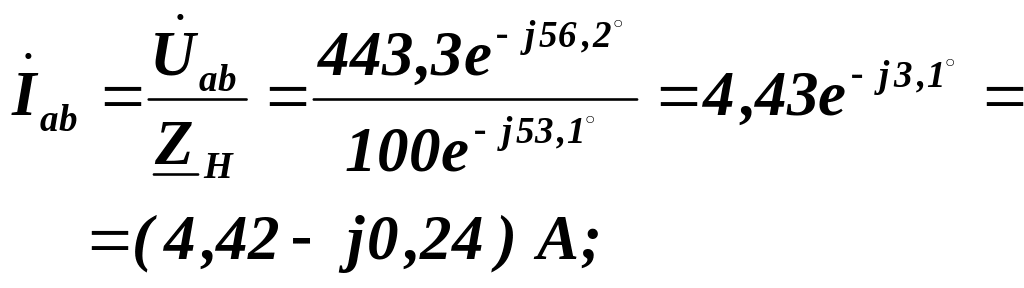
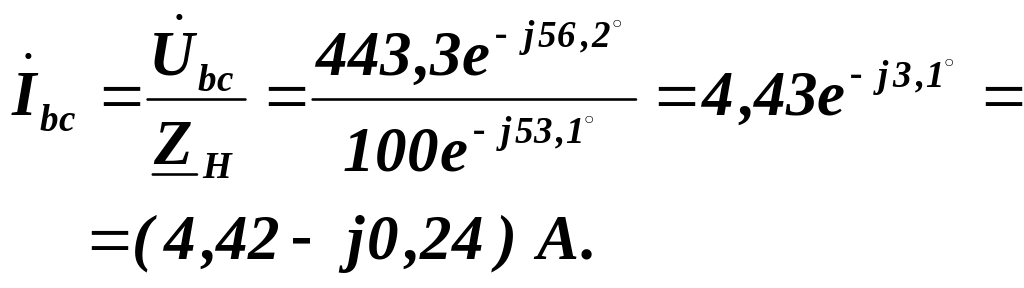
Комплексні струми та виявились рівними, так як після обриву лінійного проводу виявились сполученими послідовно фази та приймача і через них протікає один і той же струм:

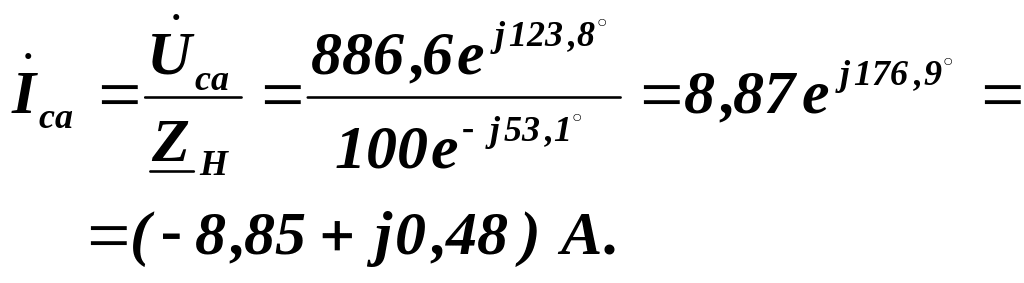
Перевірку правильності обчислень комплексних струмів виконаємо, склавши рівняння першого закону Кірхгофа для вузла « » приймача:

Комплексна потужність несиметричного приймача:

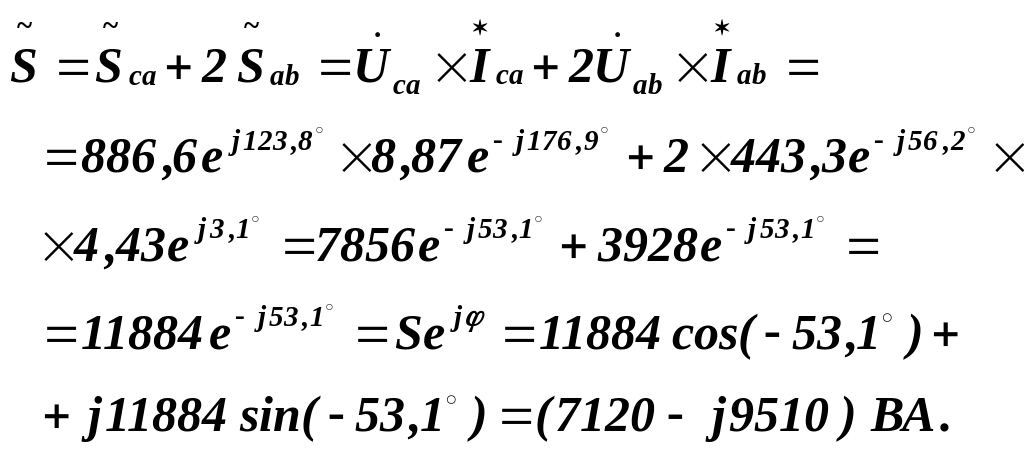
Отже, трифазний несиметричний приймач споживає:

активну потужність ; реактивну ємнісну потужність .

Повна (установлена) потужність приймача

Використовуючи обчислені значення комплексних напруг і струмів, будуємо на комплексній площині топографічну векторну діаграму (рис. 3.26).

Вектори фазних і лінійних напруг генератора відкладаємо на комплексній площині звичайним способом (завдання 3.7.1.1).

Вектор напруги зміщення нейтралі відкладаємо з точки « »; він своїм кінцем упирається в середину вектора лінійної напруги .

Вектор фазної напруги приймача відкладаємо з точки « » у напрямку відставання під кутом , а вектор фазної напруги – в напрямку випередження піл кутом . Вектор має нульову довжину.

Вектор лінійної напруги приймача співпадає за величиною і напрямком з вектором фазної напруги , а вектор лінійної напруги рівний і направлений зустрічно вектору фазної напруги .

Вектори спадів напруг на опорах лінійних проводів й являють собою векторні різниці відповідних векторів фазних напруг генератора і приймача:

; .

Вектори струмів у лінійних проводах й рівні за модулем і знаходяться у протифазі.

Вектори фазних струмів трикутника приймача й відкладаються з точки « »; вони співпадають за напрямком і величиною.

Вектор фазного струму протилежний за напрямком векторам й і рівний подвоєній довжині кожного з них.