3.7.2. Опори приймача сполучені «зіркою» з нульовим проводом, комплексний опір якого

3 .7.2.1. Симетричне навантаження фаз (рис. 3.10)

Комплексна напруга зміщення нейтралі:

так як і дальніший розрахунок схеми такий же, як і без нульового проводу при симетричному навантаженні (завдання 3.7.1.1).

3.7.2.2. Обрив лінійного проводу (рис. 3.11)

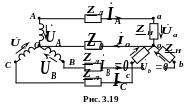
При обриві лінійного проводу « » трифазне електричне коло стає несиметричним і комплексна напруга зміщення нейтралі .

Визначаємо комплексні провідності фаз і нульового проводу:

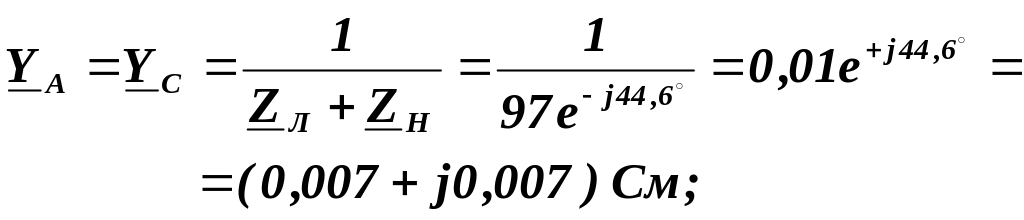
так як .

Тоді комплексна напруга зміщення нейтралі визначиться за формулою:

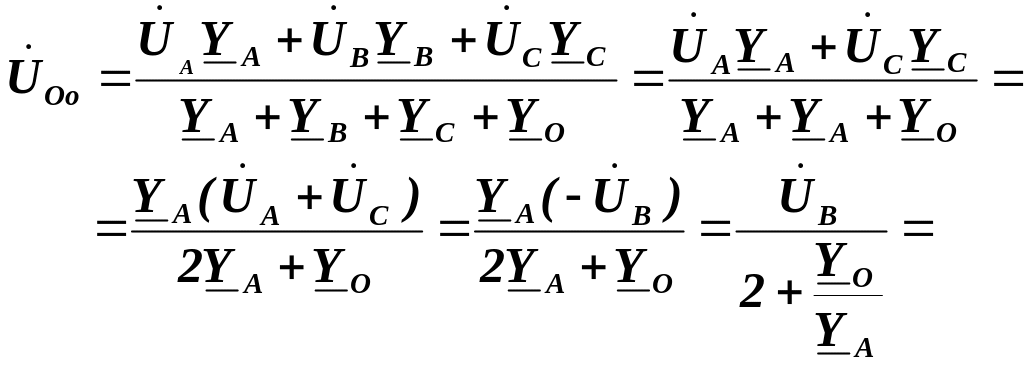
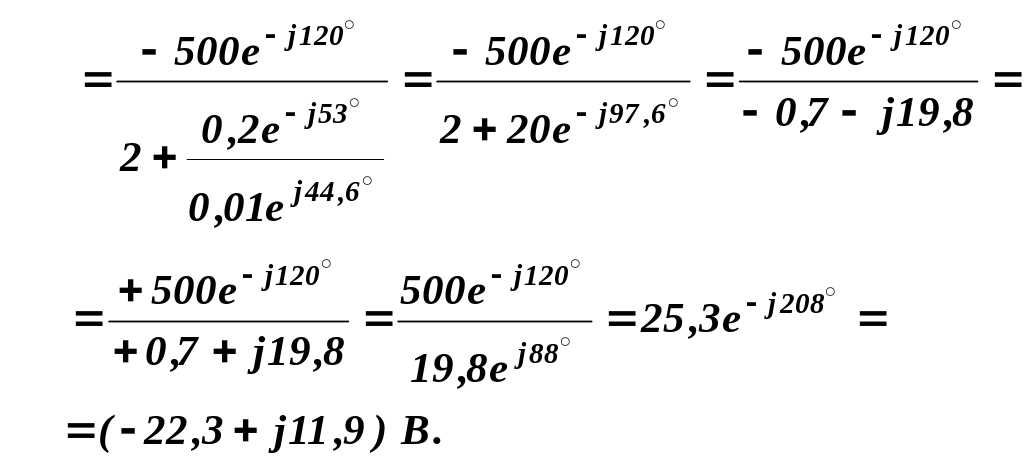
Комплексні фазні (лінійні) струми приймача визначаємо із відношень:

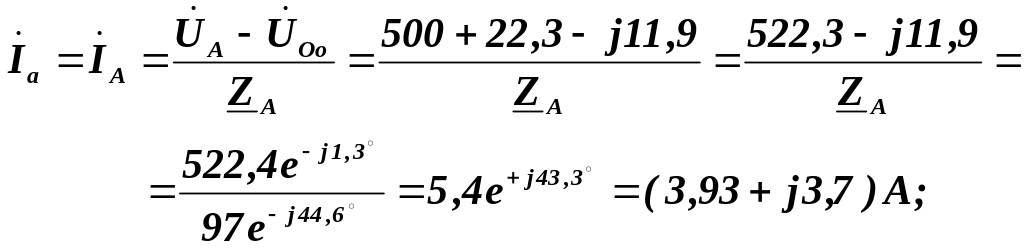
оскільки провід обірваний;

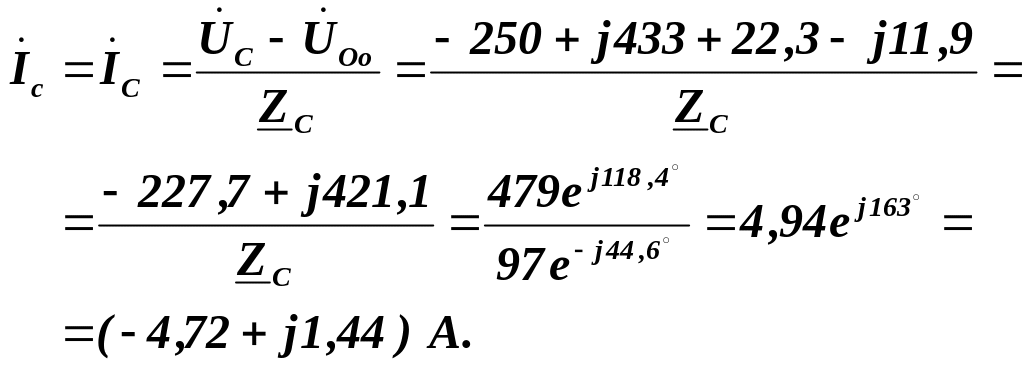
Комплексний струм у нульовому проводі:

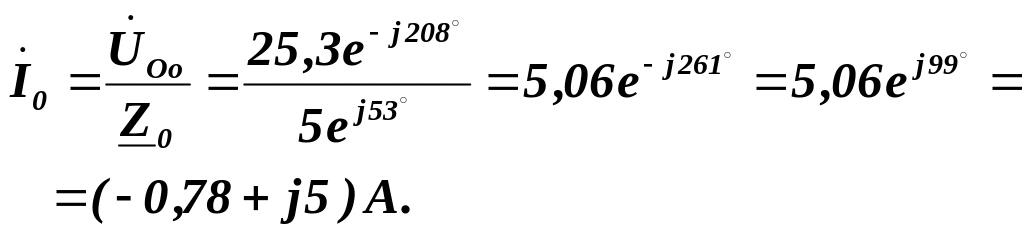
Перевірка

На підставі першого закону Кірхгофа маємо:

або

Як видно, похибка не велика.

Визначаємо комплексні фазні напруги на опорах приймача:

Комплексні лінійні напруги приймача рівні геометричним різницям відповідних фазних напруг:

Комплексні спади напруг на опорах лінійних проводів:

Комплексна потужність несиметричного трифазного споживача рівна сумі комплексних потужностей фаз:

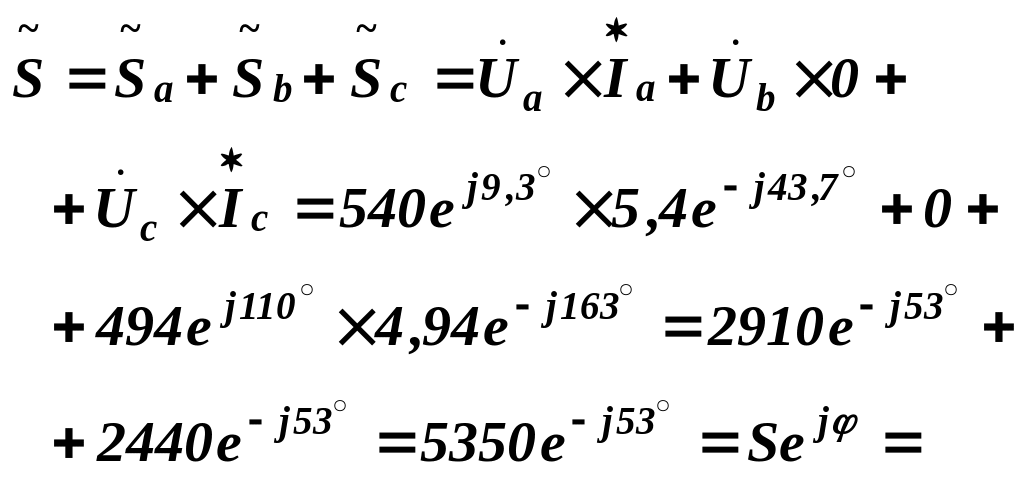
Таким чином, несиметричний трифазний приймач споживає потужності:

повну , активну і реактивну ємнісну .

Використовуючи обчислені величини струмів і напруг, будуємо топографічну векторну діаграму (рис. 3.20). Вектори фазних і лінійних напруг генератора відкладаємо аналогічно, як і при симетричному навантаженні (завдання 3.7.1.1).

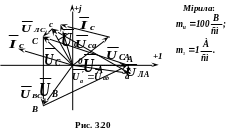
Вектор напруги зміщення нейтралі відкладаємо з точки « ». З кінця вектора (з точки « ») відкладаємо вектори фазних напруг приймача й . Вектор має нульову довжину.

Вектори лінійних напруг приймача , , відкладаємо, використовуючи векторні рівняння:

3.7.2.3. Коротке замикання фази приймача

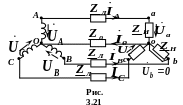
При закороченні фази приймача трифазний приймач стає несиметричним і навантаженням фази генератора буде тільки опір лінійного проводу.

Обчислюємо комплексні провідності фаз:

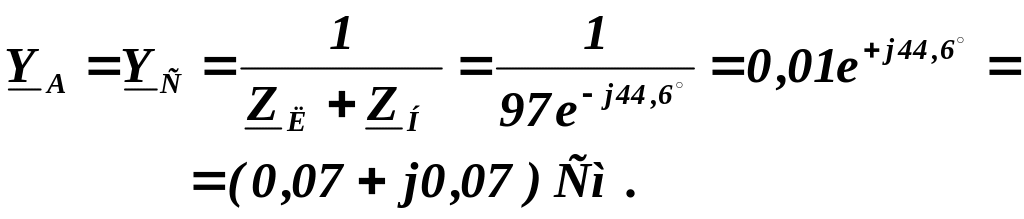
Комплексна провідність нульового проводу:

Тоді комплексна напруга зміщення нейтралі:

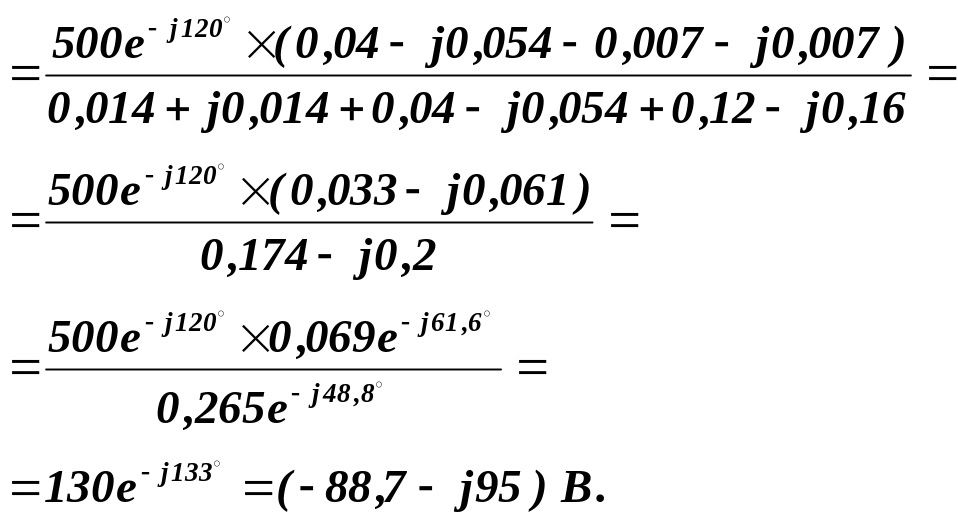
Комплексні фазні (лінійні) струми визначаємо за формулами:

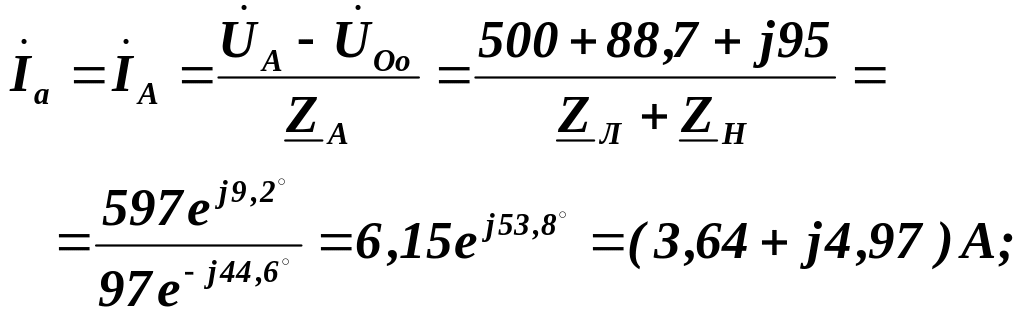
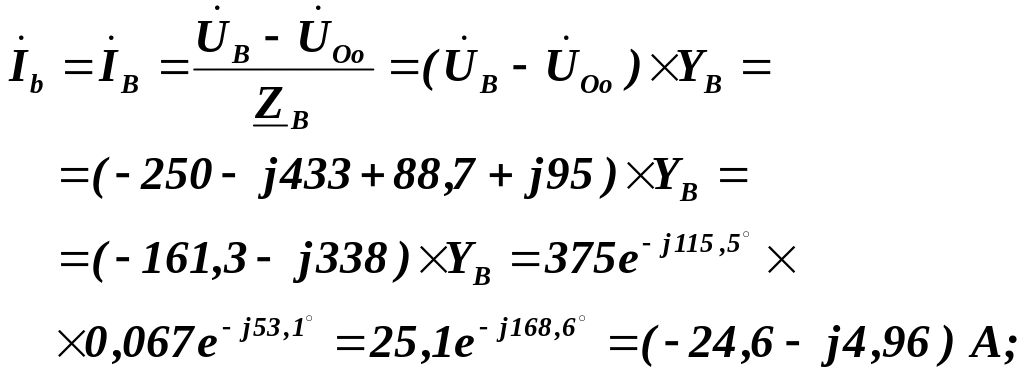
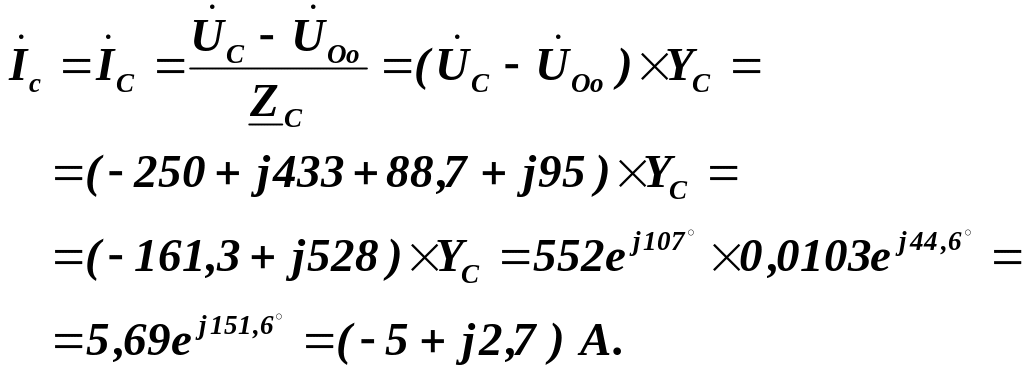
Комплексний струм у нульовому проводі:

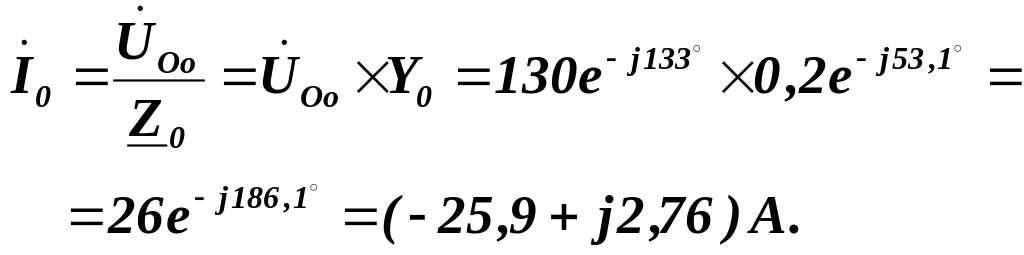
Перевірку правильності обчислень комплексних струмів виконаємо, склавши рівняння першого закону Кірхгофа для вузлової точки приймача:

Як видно, похибка незначна.

Визначаємо комплексні фазні напруги на опорах приймача:

Комплексні лінійні напруги приймача рівні алгебраїчним сумам відповідних комплексних фазних напруг:

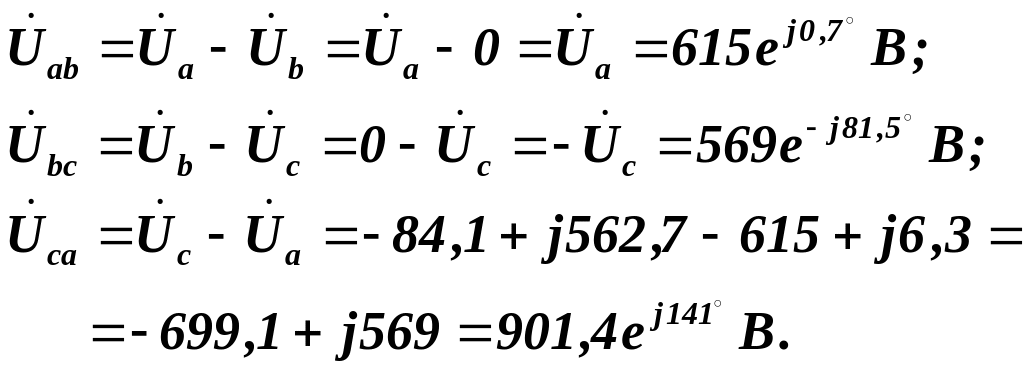
Комплексні спади напруг на опорах лінійних проводів:

Перевірку правильності обчислень комплексних напруг виконаємо, записавши рівняння другого закону Кірхгофа для контуру :

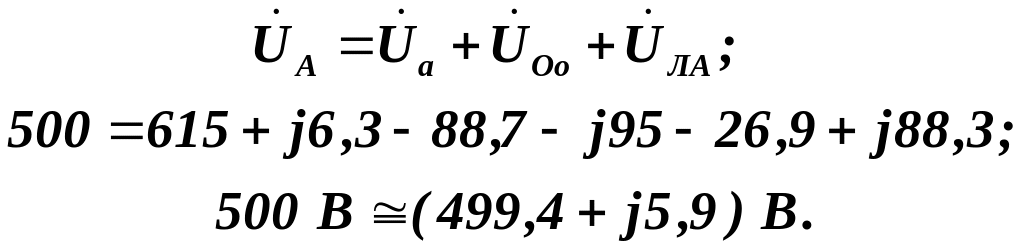
Комплексна потужність, яку споживає несиметричний трифазний приймач дорівнює сумі комплексних потужностей, споживаних усіма фазами:

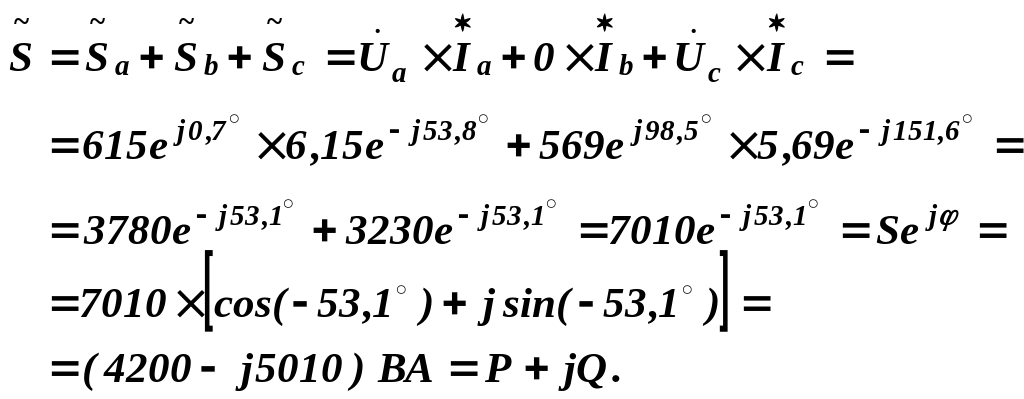
Отже, несиметричний приймач споживає потужності:

активну ; реактивну .

Повна (установлена) потужність приймача

Використовуючи обчислені значення комплексних напруг і струмів, будуємо на комплексній площині топографічну векторну діаграму (рис. 3.22).

Вектори фазних і лінійних напруг генератора відкладаємо так, як і при симетричному навантаженні (завдання 3.7.1.1).

Вектор напруги зміщення нейтралі відкладаємо з точки « » генератора у третьому октанті. З кінця вектора (точка « » приймача) відкладаємо вектори й приймача. Вектор має нульову довжину ( ).

Вектори лінійних напруг приймача , й знаходимо на діаграмі у відповідності з векторними рівностями:

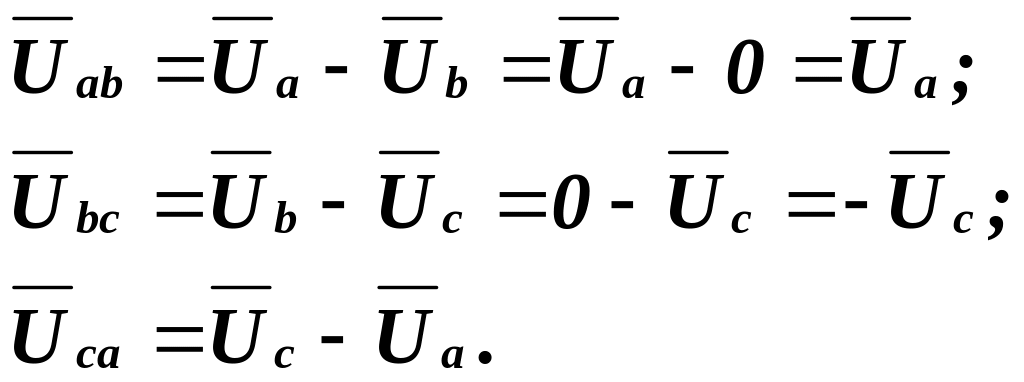
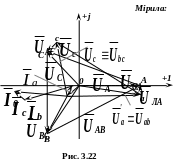
Звідси випливає, що вектор лінійної напруги співпадає з вектором фазної напруги приймача, а вектор лінійної напруги рівний за модулем вектору фазної напруги приймача і протилежний йому за напрямком. Вектор з’єднує кінці векторів фазних напруг й приймача.

Вектори спадів напруг на опорах лінійних проводів й відкладаємо у відповідності з векторними рівностями:

Іншими словами, вони сполучають кінці векторів й та й відповідно.

Оскільки вектор , то вектор сполучає кінець вектора зміщення нейтралі та кінець вектора фазної напруги генератора .

Вектори струмів , й , відкладаємо, враховуючи їх модулі та аргументи.