
- •1.Предмет статистической науки и ее задачи на современном этапе.
- •4..Виды статистического наблюдения.
- •2.Статистическая совокупность, ее виды. Единицы совокупности.
- •3.Этапы статистического исследования.
- •4..Виды статистического наблюдения.
- •5..Способы сбора статистических сведений.
- •6..План и программа статического наблюдения.
- •7..Статическая отчетность, принципы ее организации.
- •8. Ошибки статистического наблюдения. Методы проверки достоверности статистических данных.
- •9. Сводка статистических данных.
- •10. Понятие о группировке, ее задачи и виды.
- •11.Принципы построения группировок.
- •12.Ряды распределения, их виды.
- •13. Статистические таблицы, виды, правила построения и оформления.
- •14. Классификация статистических показателей.
- •15. Абсолютные статистические величины, виды правила построения и оформления.
- •16. Относительные величины, способы их расчета.
- •17Сущность и значение средних величин, их виды
- •18.Средняя арифметическая, ее методы расчета и основные математические свойства.
- •19 .Средняя гармоническая и другие
- •20. Мода и медиана, способы их
- •21. Статистическое изучение вариации. Показатели вариации и методы их расчета.
- •23 Дисперсия альтернативного признака.
- •24 Виды дисперсии и правило их сложения.
- •24.Виды дисперсии и правило их сложения.
- •25 Сущность выборочного наблюдения.
- •27Ошибки выборки и методы их расчета.
- •28Определение необходимой численности выборки.
- •3 1. Показатели динамического ряда, способы их счета и взаимосвязь. Для углубленного изучения процессов во времени рассчитывают показатели динамического ряда.
- •33.Понятие тенденции ряда динамики и методы её выявления
- •34.Сезонные колебания и методы их изучения
- •35 Сущность индексов.
- •36 Индивидуальные и сводные индексы. Принципы построения системы взаимосвязанных агрегатных индексов.
- •37 Средние индексы и их виды.
- •38 Индексный метод анализа динамики среднего уровня (Индексы переменного постоянного состава и структурных сдвигов).
- •Ряды индексов с постоянной и переменной базами сравнения, с постоянными и переменными весами.
- •40.Взаимосвязи индексов.
- •41. Территориальные индексы.
- •42. Измерение связей между социально-экономическими явлениями
- •43. Методы измерения связей.
- •45 Линейный коэффициент корреляции.
- •46 Понятие криволинейной зависимости, оценка тесноты связи при криволинейной зависимости.
- •47 Понятие о множественной корреляции.
18.Средняя арифметическая, ее методы расчета и основные математические свойства.
Средняя арифметическая - частное от деления суммы вариант на их число. Она бывает следующих видов: простая или взвешенная.
Средняя арифметическая простая, рассматривается в случае, когда известны все значения признаков х1, х2, , хп и рассчитывается по формуле
где n - число вариант;
х - значение признака.
Средняя
арифметическая взвешенная, ,
исчисляется, если известны отдельные
значения признаков и их частоты, по
следующей формуле:
,
исчисляется, если известны отдельные
значения признаков и их частоты, по
следующей формуле:
где х - значение признака;
f - частота, которая может быть абсолютной (в разах) и относительной (доля, удельный вес частот во всей совокупности) величиной.
Средняя арифметическая имеет следующие свойства:
произведение средней арифметической на сумму частот равно сумме произведений вариант на соответствующие им частоты;
если все варианты уменьшить или увеличить на одно и то же постоянное число, то средняя арифметическая из этих вариант уменьшится или увеличится на то же самое число;
если все варианты увеличить или уменьшить в одно и то же число раз, то средняя арифметическая увеличится или уменьшится во столько же раз;
если все частоты одинаково увеличить или уменьшить в одно и то же число раз, то средняя арифметическая не изменится;
сумма отклонений вариант от их средней арифметической величины равна нулю.
19 .Средняя гармоническая и другие
виды средних. Обусловленность выбора средней характером исходной информации.
Средние гармонические величины
Средняя
гармоническая —
это величина, обратная средней
арифметической из обратных значений
признака. Различают
среднюю
гармоническую
простую и взвешенную.Средняя
гармоническая взвешенная  применяется
тогда, когда статистическая
информация
не содержит частот по отдельным вариантам
совокупности, а представлена как их
произведение.
применяется
тогда, когда статистическая
информация
не содержит частот по отдельным вариантам
совокупности, а представлена как их
произведение.
Средняя арифметическая и средняягармоническая величины могут применятся в одних и тех же ситуациях, но по разным данным. Если в ИСС неизвестен числитель,то в расчетах применяется средняя арифметическая величина. Если в ИСС неизвестен знаменатель, то в расчетах используется средняя гармоническая величина
Другие виды средних величинВ статистике применяются различные виды средних величин: Средняя арифметическаяСредняя гармоническая.Средняя геометрическая.Средняя квадратическая.Мода, медиана и др. Наиболее распространенным видом средних величин в статистике является средняя арифметическая. Реже применяется средняя
гармоническая. При исчислении среднихтемпов динамики используется средняя геометрическая, а при исчислении показателей
колеблемости величины признака применяется средняя квадратическая.
20. Мода и медиана, способы их
вычисления.
Мода — это наиболее часто
встречающийся
вариант ряда. Мода применяется, например,
при определении размера одежды, обуви,
пользующейся наибольшим спросом у
покупателей. Модой для дискретного
ряда является варианта, обладающая
наибольшей частотой. При вычислении
моды для интервального вариационного
ряда необходимо сначала определить
модальный интервал (по максимальной
частоте), а затем — значение модальной
величины признака по формуле:![]() где:
где:
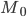 —
значение
моды
—
значение
моды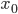 —
нижняя
граница модального интервала
—
нижняя
граница модального интервала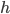 —
величина
интервала
—
величина
интервала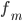 —
частота
модального интервала
—
частота
модального интервала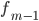 —
частота
интервала, предшествующего модальному
—
частота
интервала, предшествующего модальному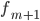 —
частота
интервала, следующего за модальным
—
частота
интервала, следующего за модальным
Медиана
— это
значение признака, которое лежит в
основе ранжированного ряда и делит
этот ряд на две равные по численности
части.Для определения медианы в
дискретном ряду при
наличии частот сначала вычисляют
полусумму частот ![]() ,
а затем определяют, какое значение
варианта приходится на нее. (Если
отсортированный ряд содержит нечетное
число признаков, то номер медианы
вычисляют по формуле:
,
а затем определяют, какое значение
варианта приходится на нее. (Если
отсортированный ряд содержит нечетное
число признаков, то номер медианы
вычисляют по формуле:
Ме = (n(число признаков в совокупности) + 1)/2,
в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).
При
вычислении медианы для
интервального вариационного ряда сначала
определяют медианный интервал, в
пределах которого находится медиана,
а затем — значение медианы по формуле:![]() где:
где:
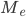 —
искомая
медиана
—
искомая
медиана— нижняя граница интервала, который содержит медиану
— величина интервала
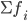 —
сумма
частот или число членов ряда
—
сумма
частот или число членов ряда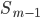 -
сумма накопленных частот интервалов,
предшествующих медианному
-
сумма накопленных частот интервалов,
предшествующих медианному— частота медианного интервала
