3.9. Температурні напруження
Розглянемо стержень, жорстко закріплений з обох кінців, рисунок 25.
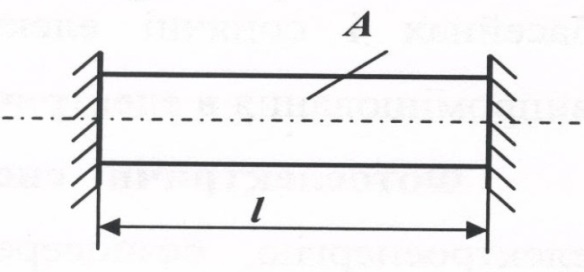
Рисунок 25. Нагрітий стержень
Нехай
відомі його механічні параметри: довжина
– l,
площа поперечного перерізу – А,
модуль Юнга І роду – Е,
коефіцієнт лінійного температурного
розширення –
.
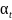Цей
стержень закріплено при температурі
,
після
чого температура піднялася на ∆t.
Треба
розрахувати напруження, які при цьому
виникають у стержні.
Розглянемо сили, які виникають у стержні. В наслідок температурного впливу стержень намагається розширитися, але це йому не вдається завдяки жорсткому закріпленню кінців, рисунок 26.
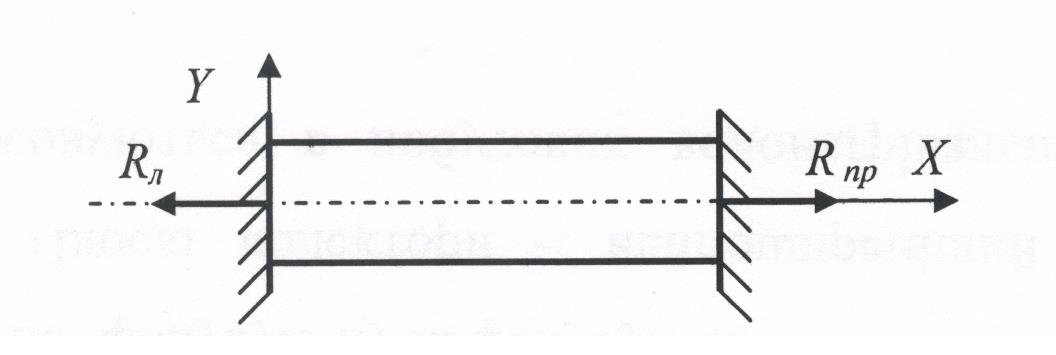
Рисунок 26. Сили, що виникають при нагріванні
Виникають
реакції опор
та
.
Розглядаючи рівновагу за допомогою рівнянь статики
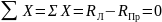, (37)
можна з’ясувати лише, що = . Рівняння статики одно, а невідомих – два.
Система один раз статично не визначена. Складаємо рівняння сумісності деформації, розглядаючи можливі температурні деформації ∆l та деформації за рахунок сил та – ∆l(R).
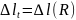(38)
або з урахуванням формули (12)
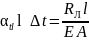(39)
тоді
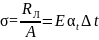. (40)
Цікавим є те, що напруження в даному випадку не залежить від довжини стержня.
Контрольні запитання
1. Що таке коефіцієнт запасу?
2. Як залежить коефіцієнт запасу від навантаження та від стану матеріалу?
4. Чистий зсув
4.1. Чистий зсув, напруження, умови міцності
Чистий зсув (або зріз) – це випадок плоского напруженого стану, коли по гранях елемента діють тільки дотичні напруження.
У цьому випадку неважко визначити величини та напрямки основних напружень, розглядаючи, наприклад, круг Мора, зображений на рисунку 27.
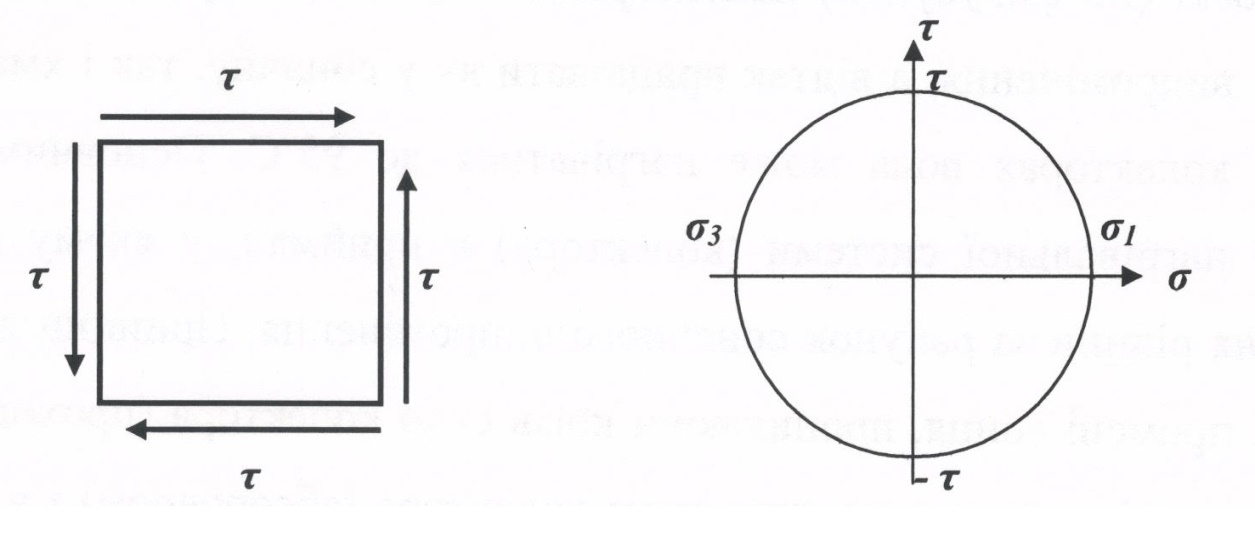
Рисунок 27. Напружений стан при чистому зсуві
Тоді цілком зрозуміло, що
;
. (41)
Якщо згадати, що
та
врахувати, що дотичні сили
,
які
викликають зсув, однакові по кожній
площадці
,
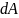то
можна записати
. (42)
Очевидно, що умовою міцності при цьому буде:
. (43)
4.2. Деформації, закон Гука при зсуві, модуль пружності іі роду
Розглянемо деформацію елемента ABCD, що знаходиться в умовах чистого зсуву, рисунок 28.
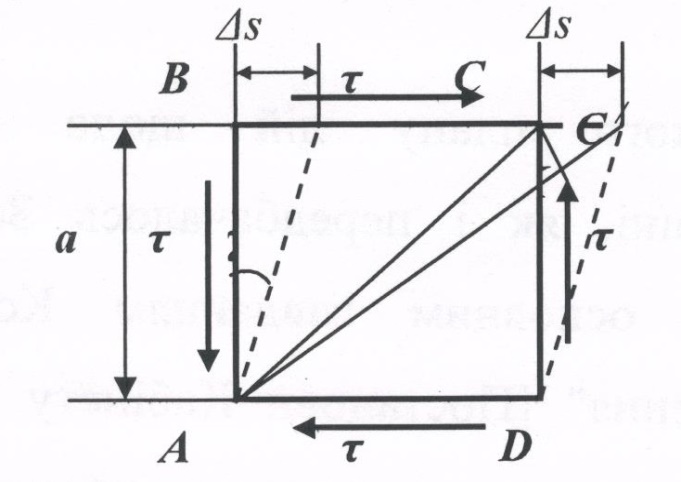
Рисунок 28. Деформації при чистому зсуву
За абсолютну деформацію при зсуві приймають величину ∆S. За відносну деформацію
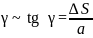. (44)
Розмірність
величини ∆S
– одиниці довжини. Відносна деформація
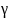– безрозмірна величина.
Розглянемо деформацію видовження діагоналі АС цього елемента.
Враховуючи, що деформації малі, маємо:
;
;
.
Тоді
. (45)
Враховуючи (45) та узагальнений закон Гука маємо:
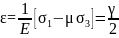, (46)
або
.
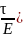Звідки
. (47)
Позначимо
. (48)
Тоді формула (47) перетвориться на
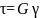, або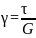 
. (49)
Залежності (49) виражають закон Гука при зсуві. Величину G називають модулем Юнга другого роду або модулем пружності другого роду чи модулем зсуву. Розмірність та фізичний зміст цієї величини аналогічні модулю Юнга першого роду Е (при розтягу–стиску).
Залежності (45) можна переписати:
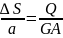або
, (50)
де Q – сила, що зсуває площадку площею А. Величина GA має такий же фізичний зміст, що й величина ЕА при розтягу–стиску, і називається жорсткістю при зсуві.