Этап 5. Моделирование временного ряда применяя методологию Бокса-Дженкинса.
Анализ динамических рядов часто показывает, что значение показателя в рассматриваемый момент времени находится в некоторой зависимости от значений в предшествующий период. Это явление носит название автокорреляции. Для обнаружения такого эффекта могут быть предложены различные методы.
Предварительный анализ АКФ, ЧАКФ:
Описательная статистика временного ряда говорит о наличии автокорреляции 4-ого порядка. Частная автокорреляционная функция имеет значимый показатель только в первом лаге, которое соответствует величине обычной автокорреляции, за исключением того, что при вычислении из нее удаляется влияние автокорреляций с меньшими лагами.
Проверим временной ряд на стационарность при помощи расширенного теста Дикки-Фуллера. Расширенный критерий Дикки-Фуллера предполагает оценить параметры модели:
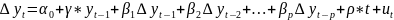
при помощи критических значений статистик Дикки-Фуллера,
где
–
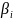коэффициенты при дополнительных лаговых
переменных;
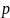– номер включенного дополнительного
лага;
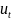– остатки без автокорреляции, т.е. «белый
шум».
В
нашем случае, мы проверяем значимость
только параметра
.
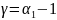Данная проверка носит название теста
на наличие единичных корней (unit-root
test). Нулевая гипотеза:
,
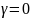т.е. ряду соответствует единичный корень
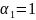(временной ряд нестационарен).
Альтернативная гипотеза: |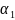
|
< 1 – временной ряд стационарен.
Для проведения теста на наличие единичных корней воспользуемся возможностями пакета Gretl:
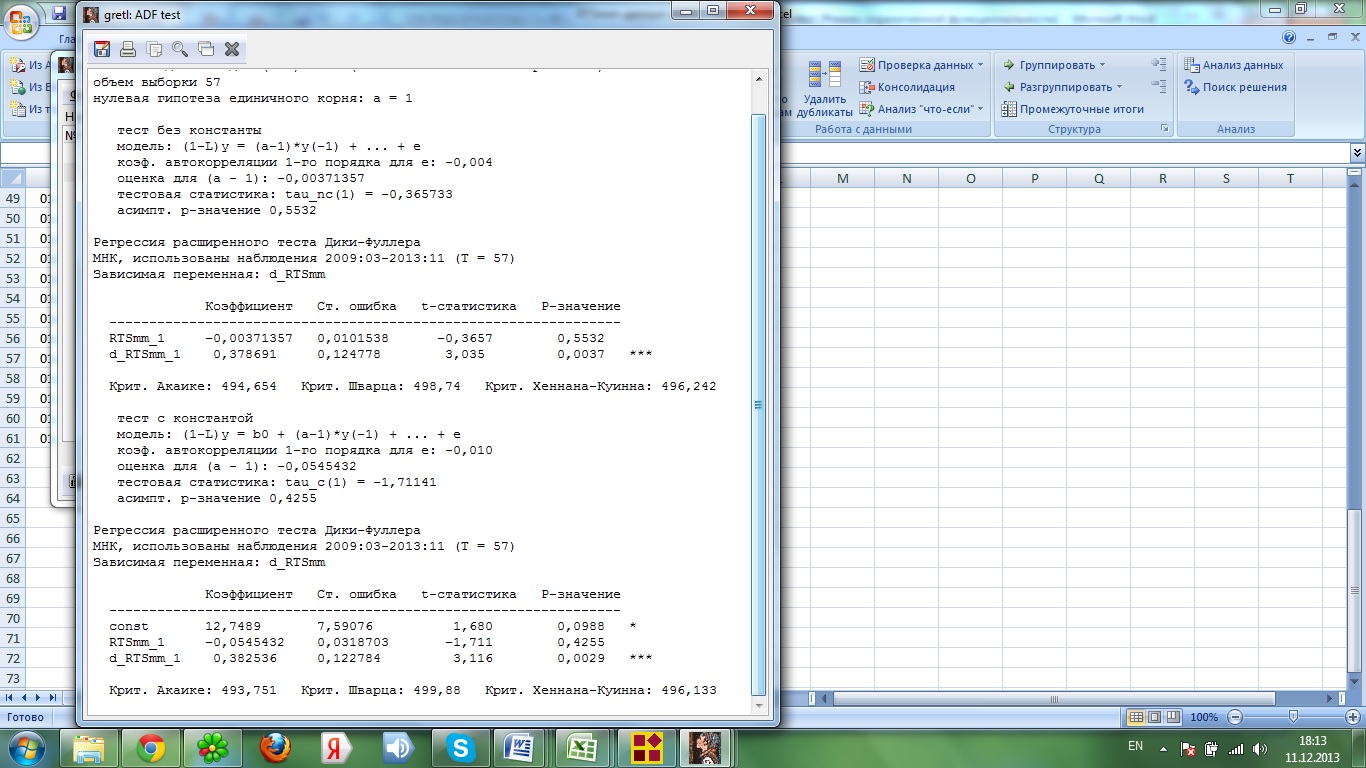
Так как в результате получили что | | < 1 следовательно Нулевая гипотеза о наличии единичного корня не отвергается, а, следовательно, исходный ряд стационарен относительно стохастического тренда.
Также
можно рассуждать следующим образом:
процесс yt
стационарен, т.к. параметр
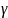получился отрицательным и по модулю
меньше единицы. Таким образом, временной
ряд относится к классу TSP
(с детерминированным трендом).
Таким образом, параметр d можно ставить равным 0.
Приведем сравнения моделей ARIMA с разными параметрами, так чтобы уменьшить среднеквадратическую ошибку RMSE:
(M) ARIMA(2,0,2) with constant
(N) ARIMA(1,2,2) with constant
(O) ARIMA(0,1,1)
(P) ARIMA(2,1,1)
(Q) ARIMA(1,1,0)
Сравнение ARIMA моделей. Показатели информационной пригодности для обучающей выборки:
Model |
RMSE |
MAE |
MAPE |
ME |
MPE |
AIC |
(M) |
16,4457 |
12,795 |
5,76696 |
-0,132622 |
-0,554979 |
5,76962 |
(N) |
17,0349 |
12,9276 |
5,86367 |
-0,675838 |
-0,110849 |
5,80612 |
(O) |
17,9361 |
14,2012 |
6,56018 |
0,673584 |
0,445207 |
5,80753 |
(P) |
17,3704 |
13,3627 |
6,13863 |
0,562579 |
0,380428 |
5,81123 |
(Q) |
17,9725 |
14,395 |
6,60831 |
0,571009 |
0,421812 |
5,81159 |
Сравнение ARIMA моделей. Тесты основных гипотез:
Model |
RMSE |
RUNS |
RUNM |
AUTO |
MEAN |
VAR |
(M) |
16,4457 |
OK |
OK |
OK |
OK |
OK |
(N) |
17,0349 |
OK |
OK |
OK |
OK |
OK |
(O) |
17,9361 |
OK |
OK |
OK |
* |
OK |
(P) |
17,3704 |
OK |
OK |
OK |
* |
OK |
(Q) |
17,9725 |
OK |
OK |
OK |
* |
OK |
Сравнение ARIMA моделей. Показатели информационной пригодности для тестовой выборки:
Model |
RMSE |
MAE |
MAPE |
ME |
MPE |
(M) |
0,213783 |
0,170591 |
0,70999 |
0,152106 |
0,529722 |
(N) |
0,222081 |
0,18117 |
0,772595 |
0,12817 |
0,576444 |
(O) |
0,242454 |
0,202589 |
0,980841 |
0,152317 |
0,73206 |
(P) |
0,242238 |
0,20239 |
0,97942 |
0,15333 |
0,737486 |
(Q) |
0,221719 |
0,173776 |
0,842998 |
0,110855 |
0,532432 |
RMSE = Root Mean Squared Error
RUNS = Test for excessive runs up and down
RUNM = Test for excessive runs above and below median
AUTO = Box-Pierce test for excessive autocorrelation
MEAN = Test for difference in mean 1st half to 2nd half
VAR = Test for difference in variance 1st half to 2nd half
OK = not significant (p >= 0,05)
* = marginally significant (0,01 < p <= 0,05)
Исходя из полученных данных выбирается модель (М). Этот показатель на всей выборке получился одним из самых маленьких на обучающей и тестовой выборке. Все параметры модели значимы, поэтому выберем для прогноза именно эту модель. Приведем ее параметры и график:
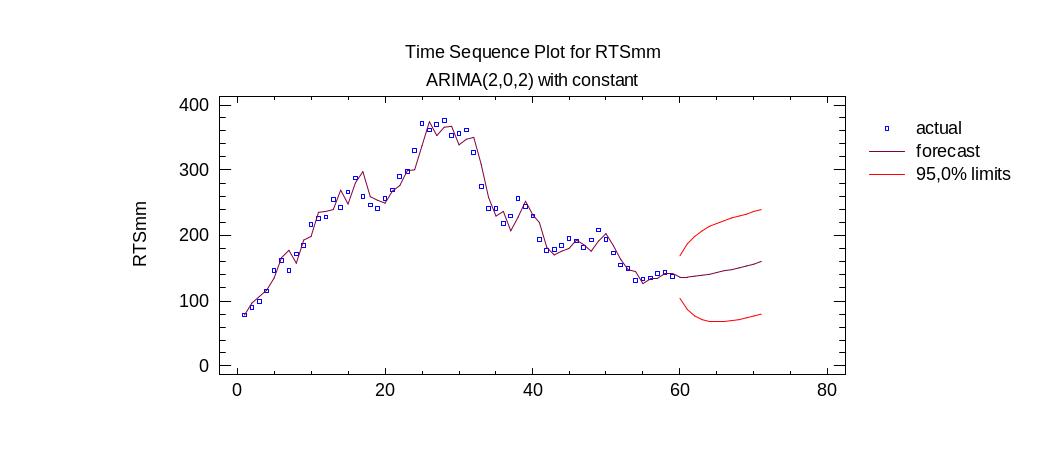
Оценка параметров модели ARIMA(2,0,2):
ARIMA Model Summary
Parameter |
Estimate |
Stnd. Error |
t |
P-value |
AR(1) |
1,92974 |
0,0361195 |
53,4267 |
0,000000 |
AR(2) |
-0,937818 |
0,0362113 |
-25,8985 |
0,000000 |
MA(1) |
0,780888 |
0,0983686 |
7,93839 |
0,000000 |
MA(2) |
0,25574 |
0,105036 |
2,43477 |
0,018236 |
Mean |
192,079 |
12,0411 |
15,952 |
0,000000 |
Constant |
1,55114 |
|
|
|
Интервальный прогноз по модели ARIMA(2,0,2):
|
|
Lower 95,0% |
Upper 95,0% |
Period |
Forecast |
Limit |
Limit |
60,0 |
136,226 |
103,071 |
169,382 |
Вычисляется
по формуле:
