Метод экспоненциального сглаживания (модель Брауна).

При использование метода экспоненциального сглаживания влияние прошлых наблюдений должно затухать по мере удаления от момента времени, для которого определяется средняя, в отличие от метода скользящей средней, где оно высчитывалось с одинаковыми весовыми коэффициентами. Простая форма модели Брауна записывается следующим образом:

где:

- текущее значение экспоненциальной средней в момент t;

α- коэффициент, характеризующий вес текущего наблюдения при расчёте экспоненциальной средней 0 < α< 1. Еще называют сглаживающим фильтром, через него устанавливается баланс между влиянием на значение текущей модельной оценки уровня ряда и предшествующих модельных оценок.

Также как и в прошлом пункте проведём серию экспериментов, анализируя зависимость точности прогнозирования от (с шагом 0,2) и применим оптимизация для модели с наилучшими показателями.

Для оценки точности прогнозирования используем те же показатели, что и в прошлом пункте, а именно:

1. Коэффициент несоответствия Тейла (K_T).

2. Стандартная ошибка модели (RMSE).

Сравнение моделей экспоненциального сглаживания Брауна:

	RMSE	КT
0,1	52,8054	0,0317
0,3	27,269	0,0176
0,5	21,3	0,0131
0,7	19,7332	0,012
0,9	20,4522	0,0127

При сравнении полученных характеристик, можно сделать вывод, что наилучшим вариантом прогнозирования на основе модели Брауна первого порядка является модель, для которой коэффициент α = 0,7. Применив для нее оптимизацию в Statgraphics получим α = 0, 7245

Построим для модели с коэффициентом α = 0, 7245 доверительный интервал прогноза на 9.2013 (60-ый месяц):

		Lower 95,0%	Upper 95,0%
Period	Forecast	Limit	Limit
60,0	148,502	110,132	186,873

который рассчитывается по формуле:

Далее проверим остатки модели на их соответствие процессу белый шум:

1. Отсутствие автокорреляции в остатках.

Авторегрессионная функция остатков модели Брауна:

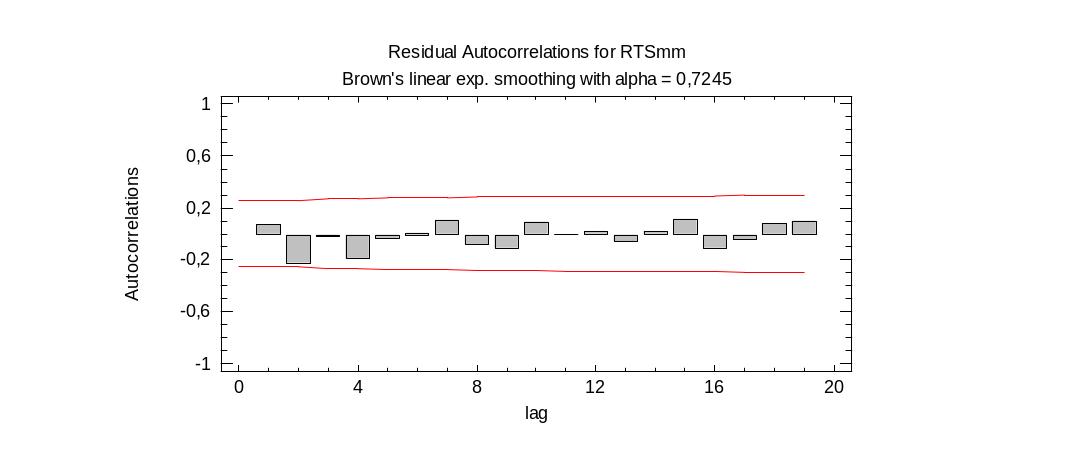
Как видно из рисунка ни одно из значений авторегрессии не получилось значимым, следовательно, остатки данной модели удовлетворяют первому условию процесса белый шум.

2. Постоянство дисперсии.

Для этого разобьем исходные данные на две подвыборки объемом 29 и 30 значений. И с помощью Statgraphics проверим гипотезу о равенстве их стандартных отклонений:

Sample sizes	30	29
Sample standard deviations	87,9202	62,6601
Null Hypothesis: ratio of variances = 1,0 Alternative: not equal Computed F statistic = 1,96877 P-Value = 0,0767335 Do not reject the null hypothesis for alpha = 0,05.

Исходя из полученных результатов, можно сказать, что наилучшая модель Брауна удовлетворяет уже двум условиям процесса белый шум. Поэтому проверим последнее.

3. Равенство нулю математического ожидания остатков.

Данная гипотеза проверяется с помощью t-статистики Стьюдента, где расчетное значение высчитывается по формуле:

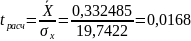
Очевидно, что полученное значение гораздо меньше табличного значения распределения Стьюдента, что доказывает гипотезу о равенстве математического ожидания остатков модели нулю.

Таким образом, все условия для процесса белый шум выполнены, данная модель пригодна для прогноза.