Государственное образовательное учреждение

высшего профессионального образования

«ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ УПРАВЛЕНИЯ»

Институт информационных систем управления

Кафедра математических методов в управлении

Лабораторная работа №1

По дисциплине «МСЭПиЭК»

Выполнила:

студентка IV курса ИИСУ

специальности

«Математические методы в экономике»

Баженова А.А.

ППроверила: С.А. Аксюк

Москва – 2013

Анализ динамики исходного временного ряда

Анализируется изменение индекса РТС Металлов и добычи (RTSmm) за период с 12.2003 – по 09.2013

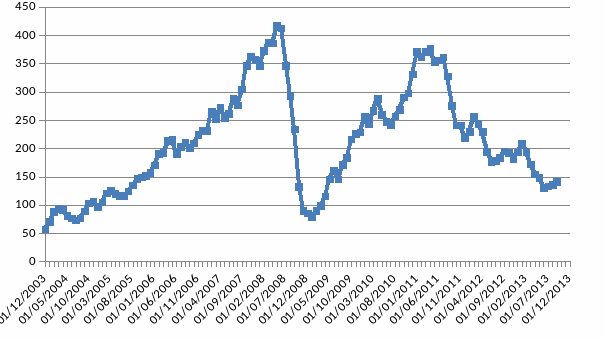
Из графика динамики исходного ряда видно, что из-за глобального экономического кризиса 2008 года, тенденция динамики индекса РТС существенно изменилась, необходимо исследовать ряд только с начала 2009 года, когда началось возобновление роста экономики, чтобы избежать влияния кризиса на модель.

График изменения индекса РТС Металлов и добычи (RTSmm) за период с 01.2009 – по 09.2013:

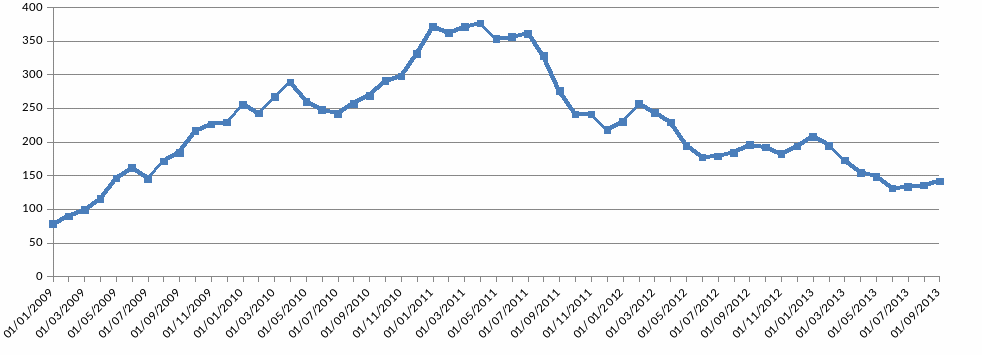
Этап 1. Проверка ряда на стационарность.

Гипотеза о равенстве средних

Делим исходные данные на 2 части (1/3 и 2/3) и проверим о гипотезу, о равенстве их средних:

	1/3	2/3
Sample means	233,318	196,01
Sample standard deviations	80,4662	65,8122
Sample sizes	20	40
Null Hypothesis: difference between means = 0,0 Alternative: not equal Computed t statistic = 1,92017 P-Value = 0,059759 Do not reject the null hypothesis for alpha = 0,05.

Формула для расчета t-статистики следующая:

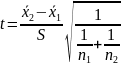
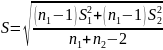
Из результатов, полученных в Statgraphics можно сделать вывод о том, что нулевая гипотеза о равенстве средних двух подвыборок не отвергается. Таким образом, можно сделать вывод о возможной стационарности процесса.

Гипотеза о равенстве дисперсий.

Так же воспользуемся Statgraphics:

	1/2	1/2
Sample standard deviatios	87,9202	62,6601
Sample sizes	30	30
Null Hypothesis: ratio of variances = 1,0 Alternative: not equal Computed F statistic = 1,96877 P-Value = 0,0767335 Do not reject the null hypothesis for alpha = 0,05.

Для сравнения дисперсий применяется критерий Фишера, для этого рассчитывается значение F-статистики по формуле:

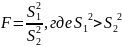
На основе, данных полученных при использование Statgraphics можно сделать вывод, что нулевая гипотеза о равенстве средних не отвергается, что говорит о возможном отсутствии тенденции в ряде.

Графический анализ.

Построим график автокорреляционной функции:

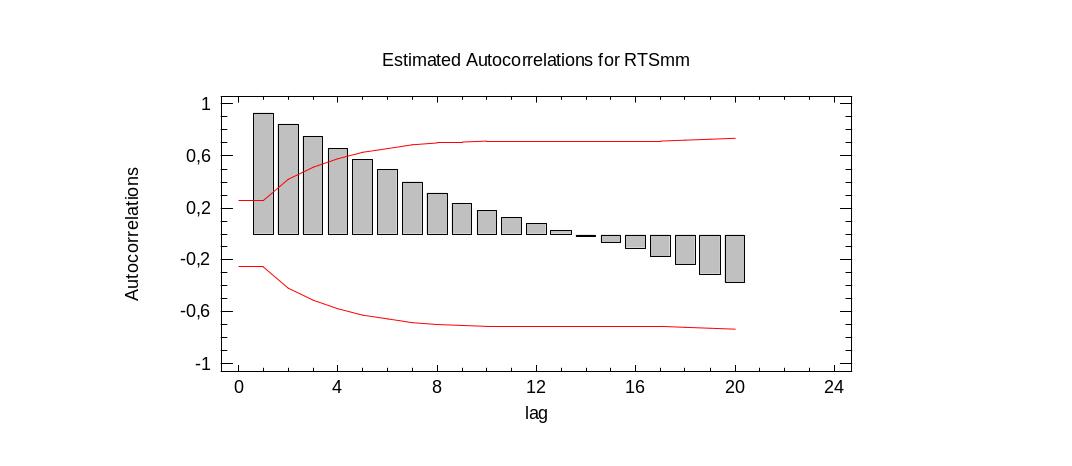
Как видно из рисунка довольно большая часть коэффициентов не значима (находится ниже линий значимости), но 4 довольно высоких значений корреляции между исходными данными и их лаговыми значениями говорит о том, что связь между ними есть, поэтому это подтверждает предположение о не соответствии данного процесса белому шуму.

Построим график частной автокорреляционной функции:

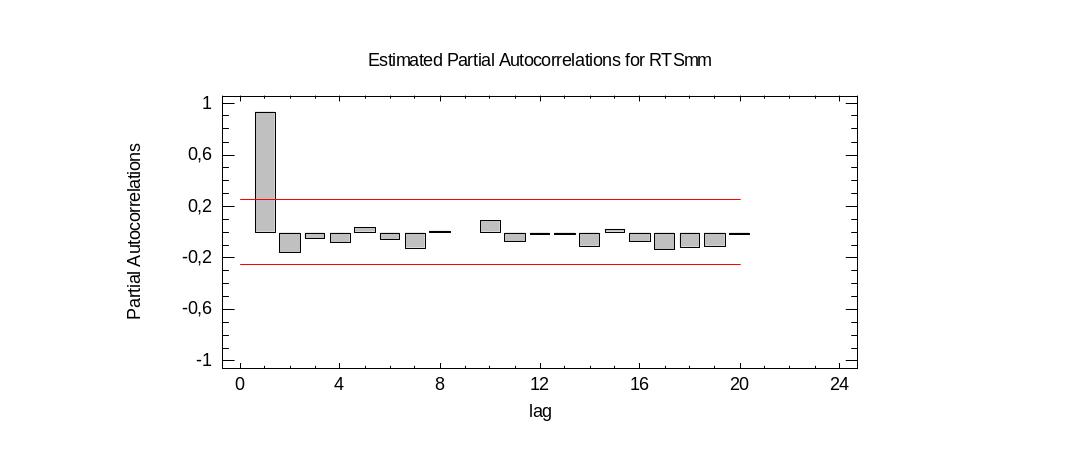
В ЧАКФ устраняется зависимость между промежуточными наблюдениями (наблюдениями внутри лага). Другими словами, частная автокорреляция на данном лаге аналогична обычной автокорреляции, за исключением того, что при вычислении из нее удаляется влияние автокорреляций с меньшими лагами. На лаге 1 (когда нет промежуточных элементов внутри лага), частная автокорреляция равна, обычной автокорреляции.

В итоге, можно заключить, что все примененные тесты показали, что в изменениях индекса РТС нельзя выделить трендовую составляющую, но нельзя говорить о соответствии изменений индекса белому шуму.