Лінійні операції над векторами в базисі

Лінійні операції над векторами визначаються так:

(4.6)

(4.7)

Приклад 1. Дано вектори Знайти





Довжина вектора

• довжина вектора

(4.8)

• якщо маємо вектора : А(х₁, у₁, z₁), В(x₂, y₂, z₂), то його довжина

(4.9)

П.6 Скалярний, векторний та мішаний добутки векторів.

6.1 Скалярний добуток та його властивості

Скалярним добутком двох векторів і називається число, що дорівнює добутку довжин векторів на косинус кута  між ними:

(4.10)

Відмітимо, що добуток | |∙cosα являє собою алгебраїчне значення ортогональної проекції вектора на напрямок вектора (позначають =| |∙cosα). Тому мають місце рівності:

∙ = | |∙ = | |∙ . (4.11)

Алгебраїчні властивості скалярного добутку

1) 2)

3) 4)

Геометричні властивості скалярного добутку

1. = 0 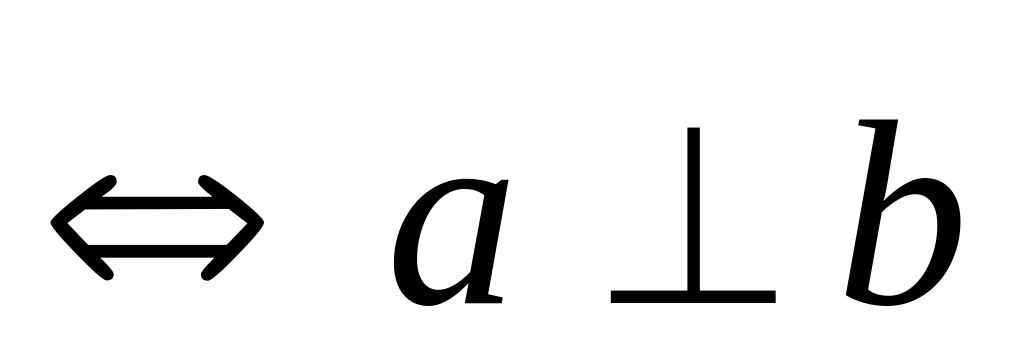– умова перпендикулярності векторів;

2. > 0 – гострий кут;

3. < 0 – тупий кут.

Скалярний добуток в ортонормованому базисі

У базисі скалярний добуток векторів

дорівнює сумі добутків їх відповідних координат:

(4.12)

Деякі важливі формули

• косинус кута між векторами і

(4.13)

• необхідна й достатня умова перпендикулярності двох векторів:

 (4.14)

проекція вектора на вектор (рис. 4.11): (4.15)

Рис. 4.11

Приклад 2. Вектори і утворюють кут Знайти:

1) 2) 3) 4)

 1) 2)

3)

4) 

Приклад 3. Дано вершини трикутника А(1, 3, 0); В(0, 1, –2); С(–1, 2, 2). Визначити його внутрішній кут  при вершині B.

 Знайдемо вектори = (1, –2, 2), = (–1, –1, 4) та їх довжини:

За формулою (4.13) обчислимо косинус кута  між векторами:



Приклад 4. При якому m вектори взаємно перпендикулярні?

 Необхідна й достатня умова перпендикулярності двох векторів:



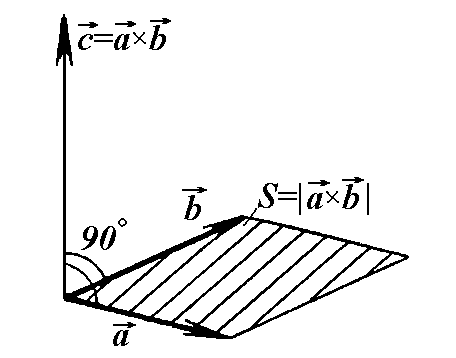
6.2. Векторний добуток векторів.

П рава трійка Ліва трійка Рис. 4.12	Упорядкована трійка некомпланарних векторів називається правою (лівою), якщо після зведення до спільного початку найкоротший поворот від вектора до вектора , що спостерігається з кінця вектора , здійснюється проти обертання стрілки (за стрілкою) годинника (рис. 4.12).
Рис. 4.13 Векторний добуток векторів і	Векторним добутком векторів і називається вектор , що задовольняє умови (рис. 4.13): довжина вектора дорівнює добутку довжин векторів і на синус кута між ними ( ); вектор перпендикулярний кожному із векторів і тобто вектор напрямлений так, що вектори утворюють праву трійку.