Расчет вектора коэффициентов множественной линейной регрессии

Линейная модель множественной регрессии имеет вид:

(1)

где i – индекс наблюдения.

Коэффициент регрессии a_j показывает, на какую величину в среднем изменится результативный признак y, если переменную x_j увеличить на единицу измерения.

Анализ уравнения (1) и методика определения параметров становятся более наглядными, а расчетные процедуры существенно упрощаются, если воспользоваться матричной формой записи уравнения (1):

,

где y — вектор-столбец зависимой переменной размерности n×1, представляющий собой n наблюдений значений y_j;

X — матрица n наблюдений независимых переменных x₁, x₂, x₃, ..., x_m, размерность матрицы X равна n×(m+1);

a — подлежащий оцениванию вектор неизвестных параметров размерности (m+1) ×1;

e — вектор случайных отклонений (возмущений) размерности n×1.

Таким образом,

, ,

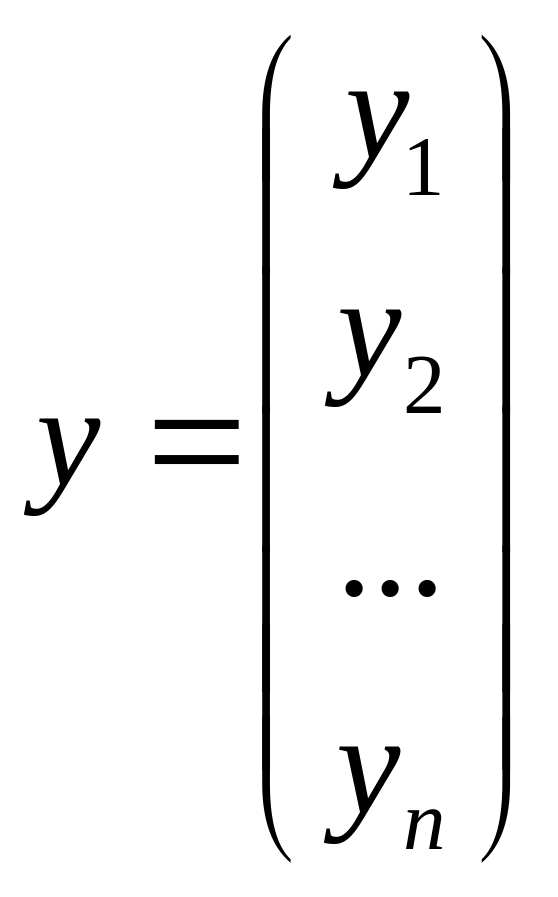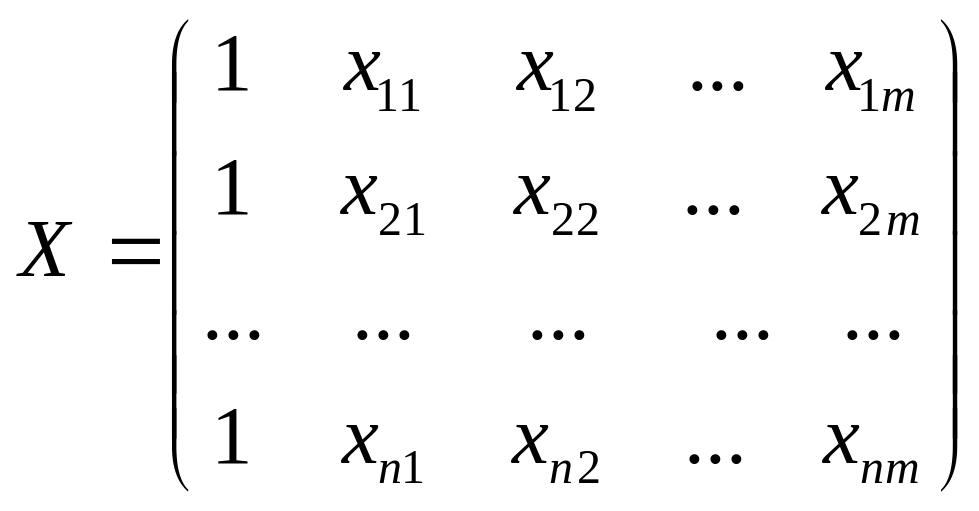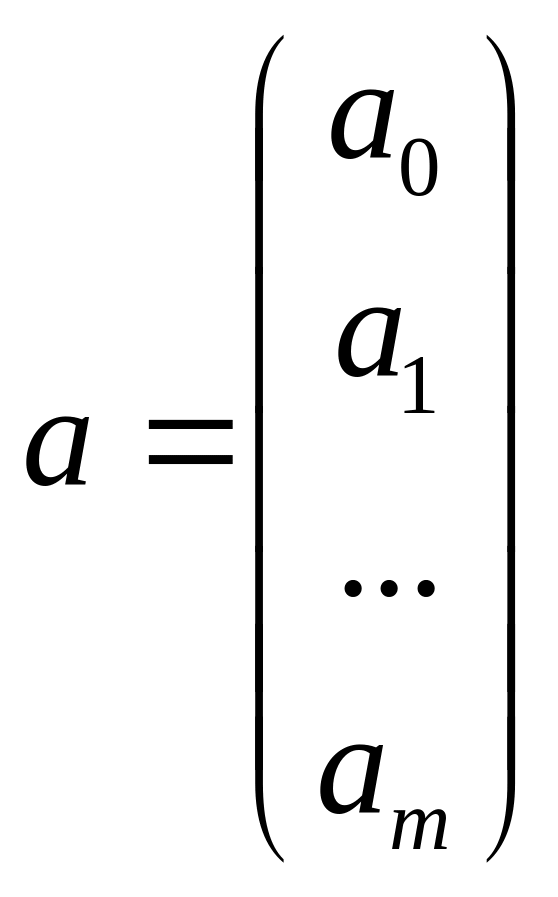
Уравнение (1) содержит значения неизвестных параметров a₀, a₁, a₂, ..., a_m. Эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки.

Формула расчета вектора коэффициентов регрессии в векторно-матричной записи имеет вид:

а = (Х^ТХ)^-1X^TY. (2)

Пример расчета.

Пусть задана таблица.

Реализация, млн. руб.	Затраты на рекламу, млн. руб.	Цена, руб.	Конкурентная цена, руб.	Индекс покупательной способности, %
y
126	4	15	17	100
148	3,8	15,2	16,8	101
274	8,2	15,5	16	104
432	14,7	18,1	20,2	107
367	19,8	15,8	18,2	108

Требуется:

1. составить по таблице матрицу X.

2. вычислить матрицу 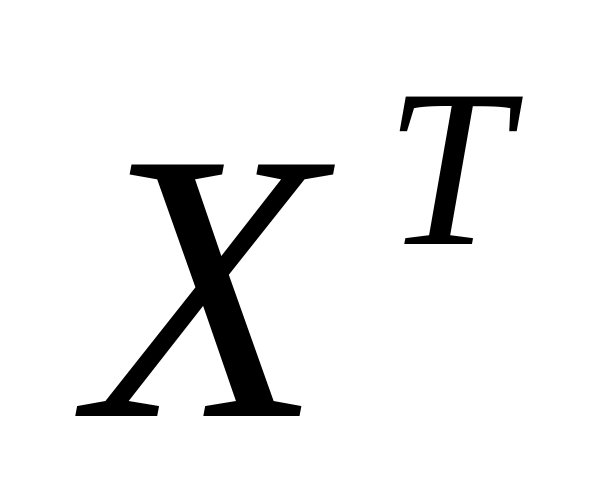. В Microsoft Excel можно воспользоваться стандартной функцией: ТРАНСП(массив).

3. вычислить 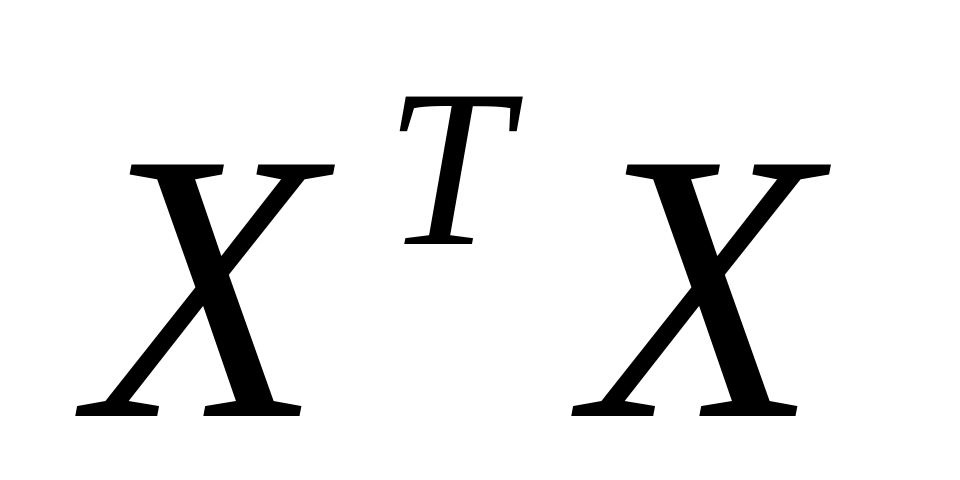. В Microsoft Excel можно воспользоваться стандартной функцией: МУМНОЖ(массив1;массив2).

4) вычислить обратную матрицу к матрице . В Microsoft Excel можно воспользоваться стандартной функцией: МОБР(массив).

5. вычислить .

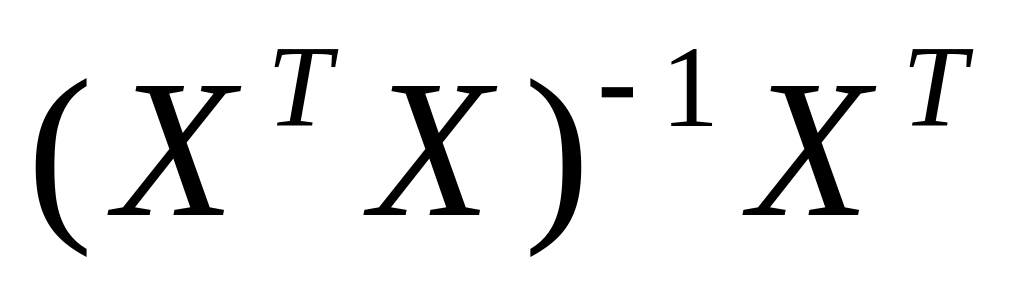5. найти вектор a, воспользовавшись равенством (2).

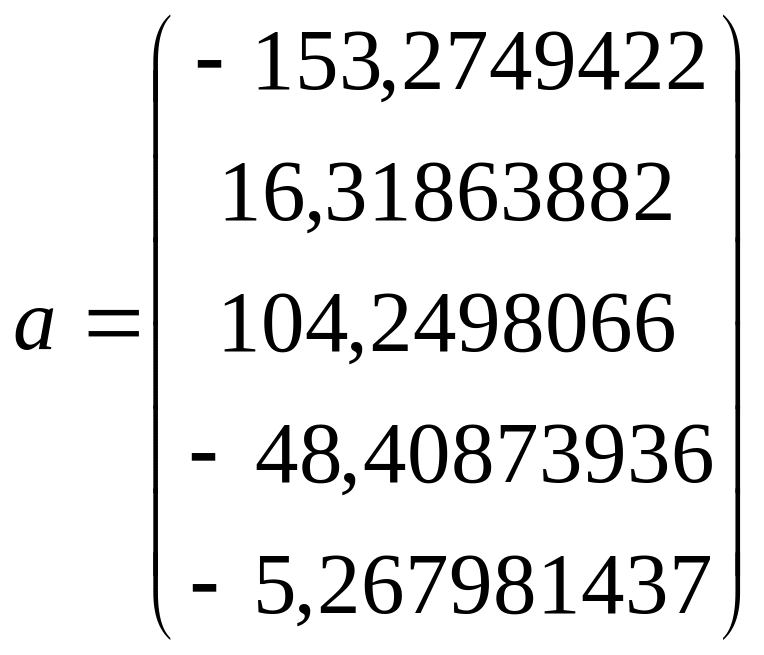
5. найти 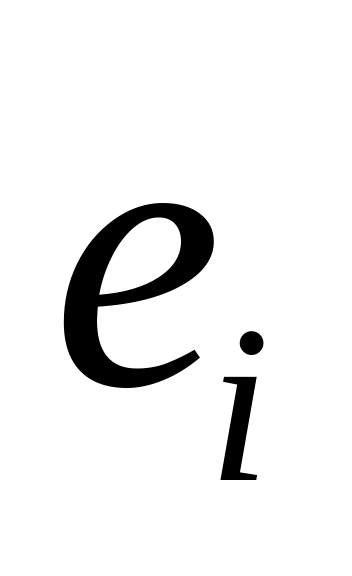– наблюдаемые значения ошибок (они должны быть близки к нулю).

=	-1,76392E-08
=	-1,88631E-08
=	-1,80848E-08
=	-1,8566E-08
=	-1,80653E-08

8. так как коэффициенты должны быть близки к нулю, то равенство (1) можно представить в виде:

.

Значения коэффициентов должны мало отличаться от коэффициентов . Найдем коэффициенты .

	126
	148
	274
	432
	367

26