Линейная и временная связь стохастических переменных

После выявления причинно-следственных связей между событиями и результатами важно определить зависимость или корреляцию между событиями и временную задержку между ними.

Напомним методику.

Корреляция. Для выявления степени корреляции между n парами данных для переменных и , , ,…, эти данные наносятся на график (диаграмму рассеяния) и для них вычисляется коэффициент корреляции по следующей формуле:

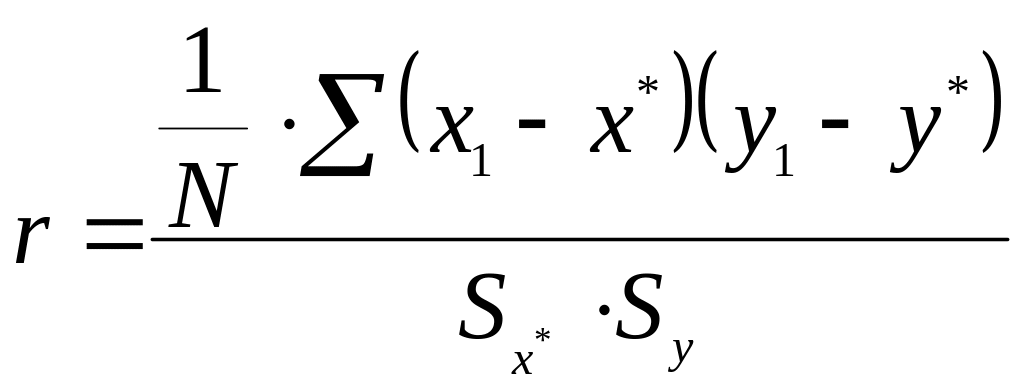
где представляют собой соответственно стандартные отклонения и :

,

Числитель в правой части выражения для r называется ковариацией.

По диаграмме рассеяния, называемой еще полем корреляции, проще всего определить силу связи между случайными величинами и . Ее вид, показывающий тенденцию к росту с ростом , определяет и вид корреляции:

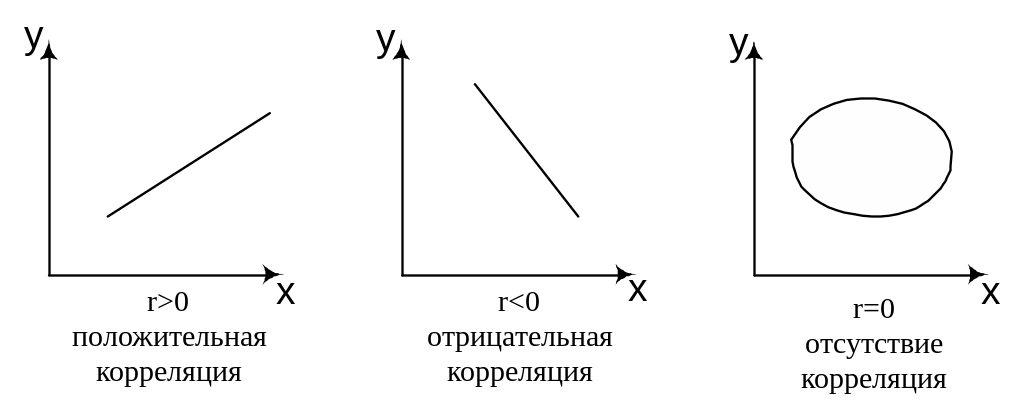
Коэффициент корреляции всегда принимает значение в интервале .Если взлеты и падения и y полностью совпадают, то , а с ослаблением совпадений уменьшается.

Однако, если нет корреляции, это не означает, что между и вовсе нет никакой зависимости, это говорит лишь о том, что между ними нет линейной зависимости.

Excel позволяет использовать 80 статистических функций (вычисление средних значений, сумм, распределений и стандартных отклонений).

Расчет временного лага.

Сведем в таблицу число жалоб населения в МЖРЭП на неисправную сантехнику (ед.) и затраты из бюджета МСУ на ремонт сантехники (тыс.руб.) по месяцам 1999 года:

	месяц
	1	2	3	4	5	6	7	8	9	10	11	12
Число жалоб	105	102	100	106	112	115	118	116	120	125	125	128
Затраты на ремонт	68	71	69	66	65	70	75	76	78	77	79	82

При использовании функции = CORREL(а1,а2) получим коэффициент – это довольно высокая корреляция. А что получится, если это соответствие сдвинуть? Если, например, имеет место смещение на 1 месяц, т.е.

, то поле корреляции будет более выраженным:

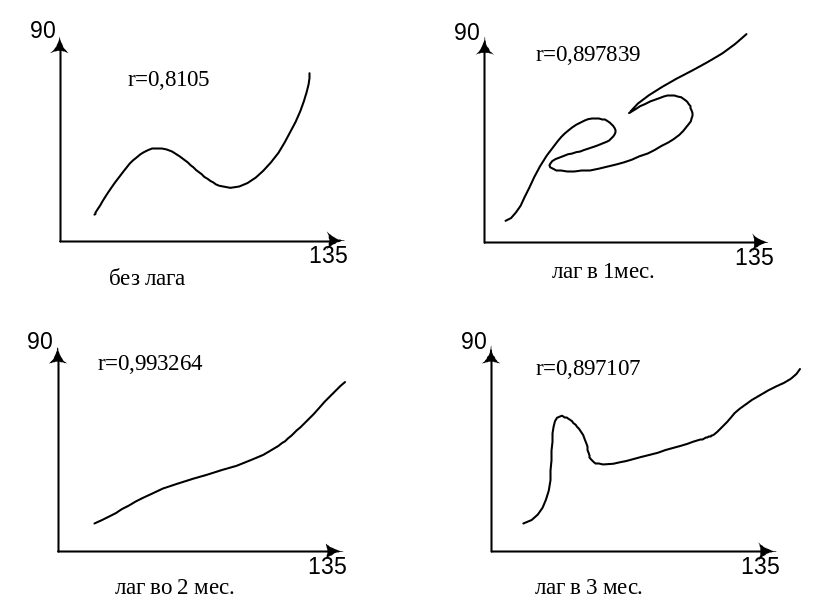
Ясно, что наивысшая корреляция достигается при временном лаге в 2 месяца. Но при этом возникает проблема определения суммы затрат . Для решения задачи используют линию регрессии и формулу ее описывающую:

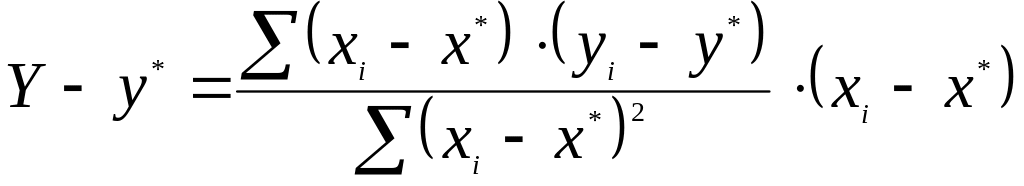(1)

для n пар данных: , ,…, .

При определении линейной зависимости между и по формуле находят значения и методом минимизации суммы квадратов разностей:

Так получена формула (1), которая при использовании в ней коэффициента корреляции r приобретает вид:

Если по данным таблицы вычислить , , , , , то можно найти предсказанное значение (прогноз) у для данного значения .

Например, значение расходов в тыс. руб. в тринадцатом месяце при временном лаге 2 месяца:

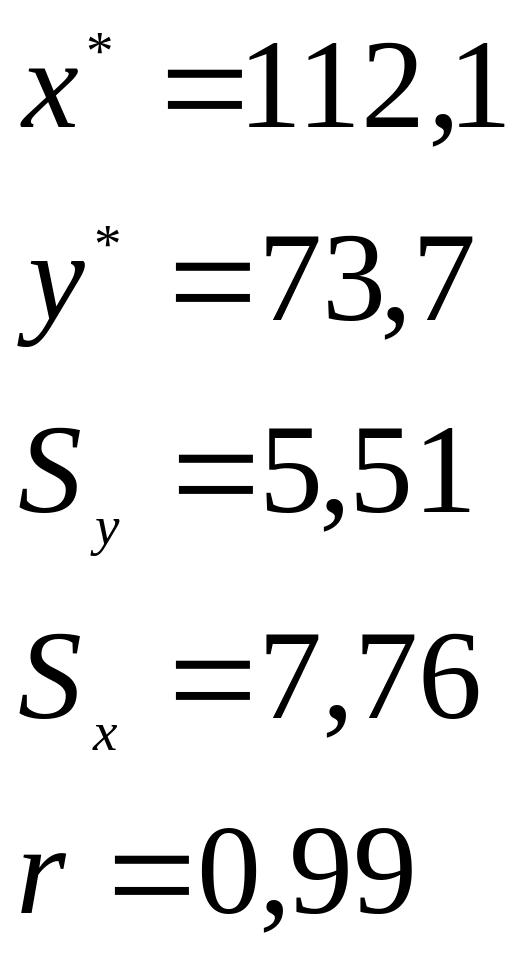
по формуле линии регрессии получим:

тогда при ,

В Excel функция LINEST (ЛИНЕЙН) вычисляет параметры линейного тренда, а функция SLOPE (НАКЛОН) – возвращает наклон линии регрессии.

Линию регрессии можно использовать эффективно, когда высок коэффициент корреляции, если , то эти рассуждения не имеют смысла.