Идентификация параметров математических моделей социально-экономических процессов

Основные понятия статистической науки: статистическая совокупность, единицы и признаки совокупности, статистический показатель, системы показателей и их взаимосвязи. Методы статистики.

Статистикой называют функцию, зависящую лишь от результатов наблюдений, поэтому любой вычисленный по эмпирическим данным показатель можно называть статистикой.

Научные основы статистики: диалектический материализм, аналогия (перенесение свойств одного предмета на другой), гипотеза (научно обоснованное предположение о возможных причинных связях между явлениями).

Специфический метод статистики основан на соединении анализа и синтеза: это выражается в 3-х стадиях цифрового освещения явлений:

1. массовое научно-организованное наблюдение для получения первичной информации об отдельных единицах (фактах) изучаемого явления - массовое наблюдение – необходимое условие освобождения от влияния случайных причин и установления характерных черт.

2. Группировка и сводка материала.

3. Обработка статистических показателей, полученных при сводке, анализ результатов для получения в текстовой (с добавление графиков и таблиц) форме выводов о состоянии изучаемого явления и закономерностях его развития.

В статистике непременно используются методы и средства математики различных уровней сложности: арифметики, теории вероятности, математической статистики.

Для статистической науки традиционны понятия:

• эмпирического ряда,

• выборки или совокупности, обозначающие одну и ту же сущность.

Выборкой называют последовательность независимых одинаково распределенных случайных величин. Элементы выборки называются вариантами. В описаниях методов обработки данных приняты понятия вектора или массива, характерные для линейной алгебры и для программирования соответственно. Если исследуемая совокупность представляет собой многомерную выборку, иначе набор векторов показателей (признаков, переменных), говорят о многомерном анализе данных.

Чаще всего приходится работать с некоторой частью совокупности, которая является выборкой из полной исходной совокупности. Поэтому различают генеральную совокупность, включающую в себя все объекты данного рода, и выборочную совокупность. Выборочная совокупность должна быть специальным (случайным) образом отобрана из генеральной совокупности и отражать основные статистические свойства последней.

Мы будем рассматривать выборочные (эмпирические) характеристики объектов и процессов.

Традиционный набор основных статистических показателей эмпирической выборки – это описательная статистика.

Группировка - расчленение всей массы случаев на однородные группы и п/группы, подсчет итогов по каждой группе, оформление результатов в виде статистических таблиц - это позволяет выделить единицы разного качества, особенности явлений, развивающиеся в разных условиях.

Сводка - обобщение данных наблюдения по выделенным частям и целому: получение статистических показателей в форме абсолютных величин (учетно-оценочные показатели), при помощи которых измеряют объемы (размеры) явлений.

Теоретический качественный анализ явления методами социально-экономических наук должен предшествовать статистическому анализу, поскольку последний осуществляет изучение (организация статистические исследования и толкование его результатов) - то есть определение состава факторов и характера их воздействия, выделение существенных различий, улавливание перехода количества в качество.

Всегда имеет место и обратное обогащение фактическими данными для иллюстрации положений наук.

Главное содержание статистики - исчисление статистических показателей и их анализ для обеспечения органов управления характеристиками объектов с целью перехода на режим предотвращения сбоев общественно-экономических процессов вместо режима устранения последствий.

Основные понятия статистики: статистическая совокупность, социальный или экономический показатель (учетно-оценочный), аналитические показатели для отражения особенностей групп рассматриваемых объектов, соотношений и взаимосвязей между ними.

Статистический показатель. Его назначение - количественная оценка свойств изучаемого явления, в нем проявляется единство количества и качества, причем, сначала определяется качественная сторона.

Учетно-оценочные показатели характеризуют уровень развития явления, его интенсивность. Аналитические показатели показывают соотношения, взаимосвязи, средние и структурные величины вариации, динамики, тесноты связи.

Статистическая закономерность. Закон больших чисел.

Закономерность проявляется в результате взаимопогашения индивидуальных отклонений от некоторого уровня, характерного для всей совокупности в целом – это сущность закона больших чисел (при исследовании данных по большому числу случаев - единиц статистической совокупности).

При взаимном уравновешивании различий отдельных единиц изучаемой массы случаев в общих средних числах выступают существенные, характерные черты и взаимосвязи явления в целом.

Совокупность действий большого числа случайных факторов приводит к результату, почти не зависящему от случая - закон выражает диалектику случайного и необходимого.

Методы выборки.

Для статистической науки традиционны понятия:

• эмпирического ряда,

• выборки или совокупности, обозначающие одну и ту же сущность.

Выборкой называют последовательность независимых одинаково распределенных случайных величин. Элементы выборки называются вариантами. В описаниях методов обработки данных приняты понятия вектора или массива, характерные для линейной алгебры и для программирования соответственно. Если исследуемая совокупность представляет собой многомерную выборку, иначе набор векторов показателей (признаков, переменных), говорят о многомерном анализе данных.

Совокупности состоят из отдельных элементов (объектов), которые объединены общностью некоторых свойств (признаков, свойств). Количество элементов совокупности называют по-разному. Если речь идет о выборке – численностью, величиной или размером, если о векторе (одномерном массиве) – говорят о размере (длине) вектора или размерности массива. Однако в многомерном анализе под размерностью часто понимают число измерений (векторов) показателей.

Чаще всего приходится работать с некоторой частью совокупности, которая является выборкой из полной исходной совокупности. Поэтому различают генеральную совокупность, включающую в себя все объекты данного рода, и выборочную совокупность.

Вся совокупность единиц, представляющая изучаемое явление – объект исследования, называется генеральной совокупностью (ГС). Часть ГС, отобранная для обследования и изучения, называется выборочной совокупностью (ВС).

ВС характеризуется: ВС ( , , ; ), которые не равны соответственно средней арифметической и частости ГС.

Для оценки точности выборочного наблюдения оценивают ошибки репрезентативности , которые не являются ошибками регистрации. ВС не достаточно точно воспроизводит свойства ГС, эта точность повышается при случайном отборе.

Выборочная совокупность должна быть специальным (случайным) образом отобрана из генеральной совокупности и отражать основные статистические свойства последней.

Если мы прогнозируем рыночные цены на картофель в зависимости от погодных условий, то мы будем находить среднюю цену картофеля на всех рынках города в прошлом году и средние температуры, объемы осадков в текущем году. Данные должны относиться к районам, связанным хорошими дорогами с городом. В итоге получим средние величины на основе выборочного метода.

Чтобы распространить результаты наблюдения на все явление в целом выборочное наблюдение надо проводить по строго определенным правилам (статистики и математики):

Название способа осуществления выборки	Основа	Отбор единиц	Оценка
Случайный отбор	Отбор путем жеребьевки.	Повторный или бесповторный.	Точность возрастает с увеличением объема выборки.
Механический отбор	Все элементы ГС располагают в любой последовательности и механически разбивают на равные части.	В определенном порядке берут 1/5 или 1/10 часть единиц наблюдения.	20% или 10% от истинного значения показателя ГС. Случайность ошибки обусловлена не способом отбора, а случайным порядком размещения изучаемых единиц в ГС.
Типологический отбор	ГС предварительно расчленяется на отдельные качественно однородные группы (типы).	Объем выборки в каждой типической группе устанавливается пропорционально ее удельному весу в ГС. , , р определяется для каждой группы отдельно	Большая точность благодаря группировке по типам
Серийный (гнездный) отбор	Когда очень большая территория обследования, отбирают наиболее типичные для данной территории населенные пункты (гнезда).	Внутри гнезда производят сплошное обследование.	Точность меньшая по сравнению с другими способами.

Итак, мы будем рассматривать выборочные (эмпирические) характеристики объектов и процессов. Традиционный набор основных статистических показателей эмпирической выборки – это описательная статистика.

Анализ эмпирических данных.

Построение рядов распределения – составная часть сводной обработки данных статистического наблюдения (ДСН) для выявления основных свойств и закономерностей статистической совокупности (СС).

Признак: качественный, количественный. Соответственно – Ряды: атрибутивный, вариационный.

На формирование уровня признака влияет большое число факторов, которые при изучении относят в 2 группы:

1. общие для всех единиц изучаемой совокупности;

2. свойственные конкретным единицам СС и определяющие их индивидуальные особенности.

Важнейший вопрос статистического исследования (СИ) – изучение характера и степени вариации у отдельных единиц СС. Важно определить роль каждой группы факторов на вариацию признака, а также роль отдельных факторов в группе.

Схема исследования СС:

• первичный ряд данных,

• его ранжирование, определение: макс, мин, размах значений признака, выделение наиболее часто появляющихся значений, разделение данных по группам, определение частоты повторений отдельных вариантов значений.

Признаки могут быть: дискретные и непрерывные.

Ряд распределения принято оформлять в виде таблицы.

Тарифный разряд рабочего Xi	Число рабочих, имеющих этот разряд fi	Частость Wi	Накопленная частота Si
2	1	0,05	1
3	5	0,25	6
4	8	0,40	14
5	4	0,20	18
6	2	0,10	20
Итого (SUM fi)	20	1,00

Частость - частота, представленная в относительном выражении Wi = fi/SUM fi.

Для того, чтобы разделить данные наблюдений по группам, можно выбрать равные или неравные интервалы разбиения.

Определение величины интервала h для построения вариационного ряда с равными интервалами:

R = Xmax – Xmin;

Количество групп определяется приближенно по формуле Стэрджесса:

k = 1 + 3.322 lg n, где n – общее число единиц изучаемой СС;

h = R/k.

Количество групп для него к= 5, интервал между группами h = 0.9

Для вариационного ряда с неравными интервалами рассчитывают относительную плотность распределения. Для сравнительной оценки данных, собранных по различным СС и по-разному обработанных, преобразуют интервалы и при этом используют показатели:

mi(a) = fi/hi – абсолютная плотность

mi(o) = Wi/hi - относительная плотность

Основные характеристики вариационного ряда для анализа и сравнения различных рядов распределения:

1. показатели центра группирования: центры группировки - мода, медиана (при одинаковых размахе вариации и характере распределения частот);

2. показатели вариации признака: пределы варьирования признака;

3. показатели формы распределения: симметричность расположения частот относительно центра (показатели асимметрии).

Графическое изображение дискретного ряда – полигон распределения (величины вариантов значения признака X, частота f (частость w) этих вариантов, например – количество купленных пар обуви 39, 40, 41 и др. размеров).

Графическое изображение интервального ряда – гистограмма, например, помесячные субсидии по квартплате. Для неравноинтервального ряда по оси ординат – показатели плотности интервалов.

При n   увеличивается число групп интервального ряда, уменьшается величина интервала, полигон превращается в кривую распределения, которая характеризует вариацию признака и закономерности распределения частот внутри однокачественной совокупности.

При сравнении вариационных рядов, для анализа концентрации (производства в экономических исследованиях) используется кумулятивная кривая (кумулята), построенная по рассчитанным накопленным частотам и частостям. Она показывает, сколько единиц СС имеют значение признака не больше, чем рассматриваемое значение.

Функции эмпирического распределения.

Эмпирической функцией распределения (функцией распределения выборки, выборочной функцией распределения) называют функцию Fn(x), определяющую для каждого значения х частотное распределение эмпирической выборки, то есть долю событий Х<=х:

Fn(x) = nx/n

Где nx - число вариант, меньших, чем х,

n - общее число вариант эмпирической выборки.

Величины nx называются накопленными (кумулятивными) абсолютными частотами, а величины nx/n называются накопленными (кумулятивными) относительными частотами. Накопленная относительная частота иногда называется также интенсивностью и может выражаться в процентах.

Показатели центра распределения.

Средняя арифметическая для дискретного ряда (x ср = SUM(xi*fi)/SUM fi), для интервального ряда (x ср = SUM(x ср интерв * fi)/SUM fi). Это основная хар-ка центра распределения, опирающаяся на всю информацию об изучаемой совокупности единиц.

Медиана (Ме) соответствует варианту, стоящему в центре ранжированного ряда. Положение Ме в ранжированном ряду определяется ее номером № Ме = (n+1)/2. Дополняет, иногда заменяет среднюю арифметическую, например, статистический контроль качества (образец, +/-) не требуется специального расчета. Еще один пример: солдатский строй – «средний» воин.

Мода (Мо) – наиболее часто встречающееся значение признака в СС. Применяется при изучении спроса населения на товары, когда интерес представляет определение модального размера, пользующегося наибольшим спросом.

Показатели вариации (колеблемости) признака.

При различиях в индивидуальных значениях признака средняя арифметическая будет ненадежной хар-кой СС.

Размах колебаний (размах вариации) R = x max – x min. Простота расчета по 2-м значениям, но для однородных СС (предупредительный контроль качества).

Среднее линейное отклонение:

Для несгруппированных данных

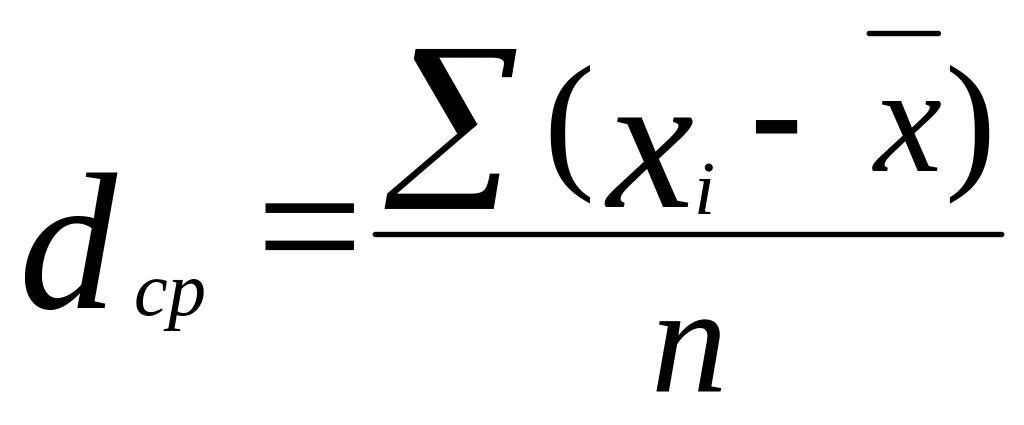
Для сгруппированных данных

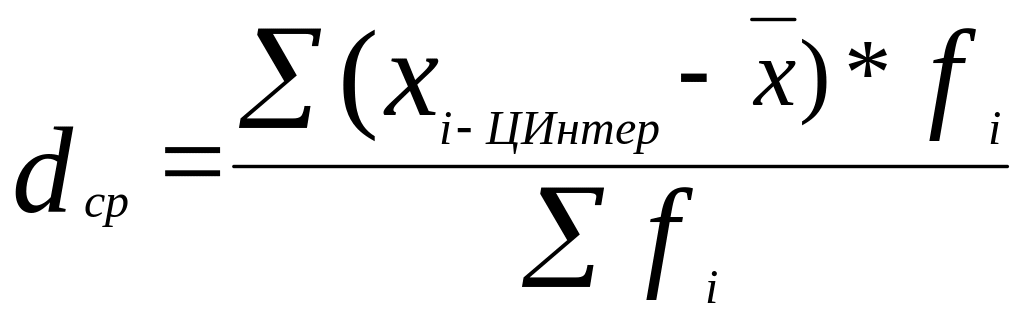
Дисперсия σ2 – средняя из квадратов отклонений вариантов значений признака от их средней величины. Дисперсия (вариация) характеризует степень отклонения вариант данной совокупности от среднего в абсолютных числах, то есть дисперсия характеризует меру разброса (рассеяния) распределения относительно среднего значения.

Для несгруппированных данных

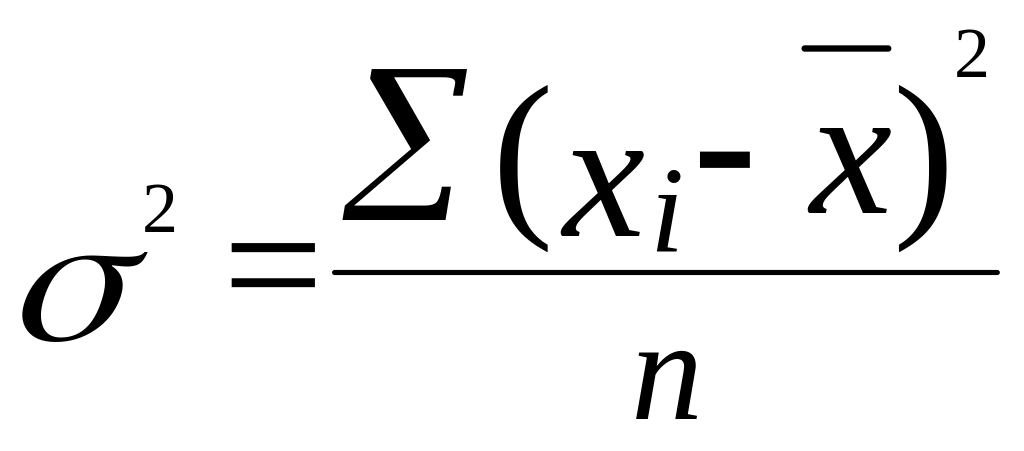
Для сгруппированных данных

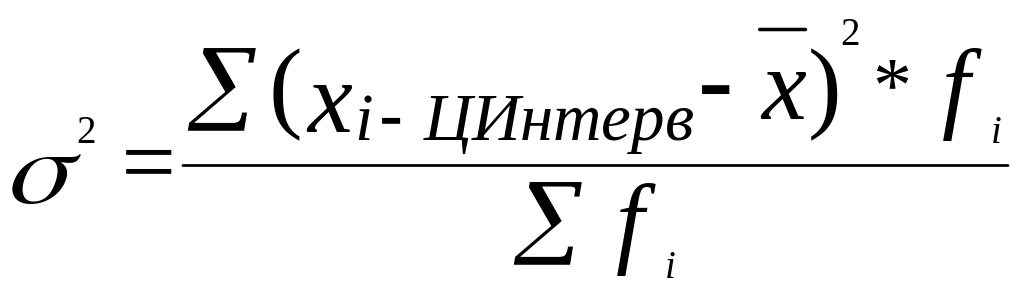
Свойства дисперсии: дисперсия постоянной величины равна нулю; если все варианты значений признака уменьшить на одно и то же число, то дисперсия не уменьшится; Если все варианты значений признака уменьшить в к-раз, то дисперсия уменьшится в к^2-раз.

Среднее квадратическое отклонение σ – корень квадратный из дисперсии.

σ2 и σ – наиболее широко применяемые показатели вариации, т.к. входят в большинство теорем теории вероятности – фундамента статистики. Кроме того, дисперсия может быть разложена на составные элементы, позволяющие оценить влияние различных факторов, обусловливающих вариацию признака.

Отклонения (и линейное тоже) показывают насколько в среднем колеблется величина признака единиц СС. При близости к нормальному или симметричному распределению существует взаимосвязь σ=1,25*d ср.

Среднее квадратическое отклонение показывает как располагается основная масса единиц СС относительно средней арифметической. Теорема П.Л.Чебышева: независимо от формы распределения 75% значений признака попадают в интервал х ср+2σ, а по крайней мере 89% всех значений попадают в интервал х ср+3σ.

При сравнении колеблемости различных признаков в одной и той же СС или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической пользуются относительными показателями вариации:

Коэффициент осцилляции Kr = (R/x ср)*100%,

Относительное линейное отклонение Kd ср = (d ср/x ср)*100%,

Коэффициент вариации v представляет собой характеристику рассеяния распределения случайной величины. Он показывает, какую долю или какой процент составляет среднее квадратичное отклонение от среднего значения.

Коэффициент вариации v = (σ /x ср)*100% - наиболее часто применяется и для сравнительной оценки вариации, и для характеристики однородности совокупности, СС считается однородной если v <= 33% (для распределений, близких к нормальному). СС характеризуется и Х ср, и коэффициентом вариации v, например, цен на жильё в разные периоды ($500/кв.м + $50 летом/ -$50 зимой).

Определение возможных пределов значений единиц генеральной совокупности исследуемых явлений.

Выборка (ее объем и тип) определяет и достоверность связей между наблюдаемыми при выборке факторами, и возможные пределы, в которых будут находиться характеристики единиц генеральной совокупности.

При выборке имеют место ошибки регистрации и ошибки репрезентативности

,

где

- корректирующий коэффициент доверия,

- средняя ошибка выборки, которая зависит от вида отбора

t – определяется по таблице критерия Стьюдента в зависимости от заданного уровня вероятности и числа наблюдений – единиц выборки (от данных задачи). При n-> ~ и для р = 0,997, t -> 3.

Для повторного отбора

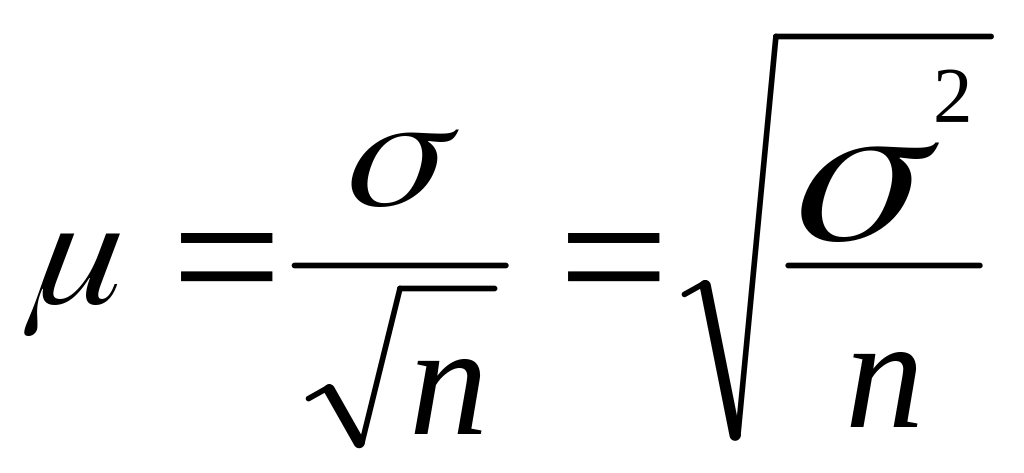
Для бесповторного отбора

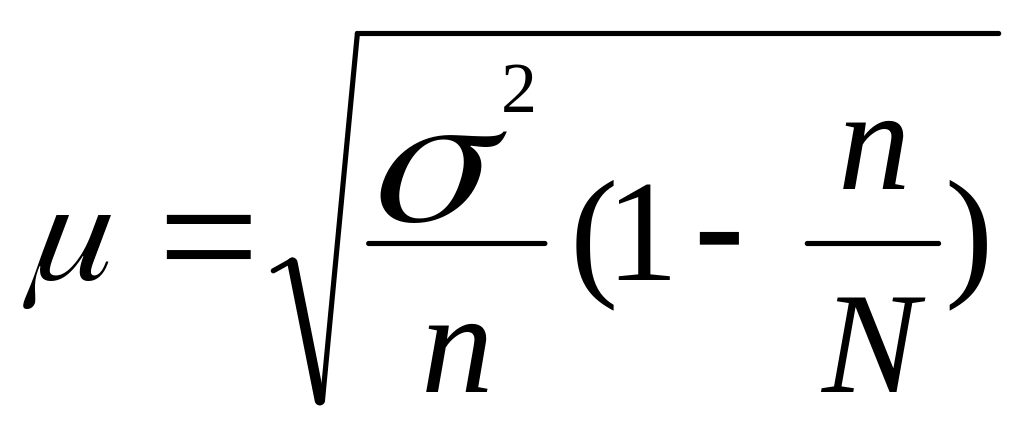
Тогда

Анализ результатов наблюдений для определения проблемных факторов и переменных в математических моделях: диаграмма «причины – результат», диаграмма Парето, АВС-анализ.

Для выбора переменных при построении математической модели объекта управления следует оценить наличие их влияния и степень этого влияния на результат управления.

Диаграммы «причины – результат»

Схемы, характеризующие зависимость между полученными результатами и признаками, воздействующими на эти результаты, именуются диаграммами «причины – результат» или схемой «рыбий скелет». Такие схемы имеют «хребет», большие, средние и малые «кости»:

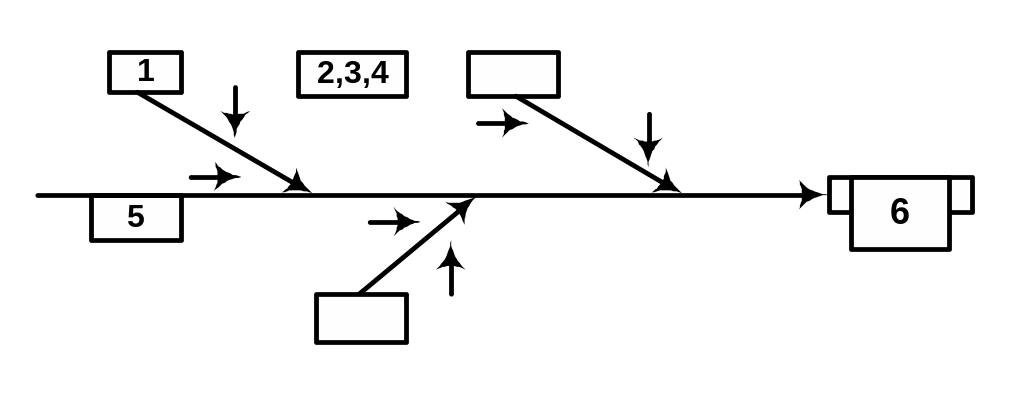
1-факторы (причины)

2, 3, 4 – малая, средняя и большая кости – взаимосвязи факторов, ресурсов и условий, выражаемые в показателях предметной области

5 – хребет – основа общности показателей ситуации

6 – характеристика (результат) ситуации

В качестве результата управления рассматривается состояние снятия проблемы, хребет схемы – это объект, в котором выявляется проблема, факторы – источники появления проблемы: производство, испытания, снабжение ресурсами, условия эксплуатации. В этом случае «кости» будут означать отдельные стороны факторов, зависящие от разных ресурсов, субъектов, времени, условий.

Для глубокого анализа основных факторов необходимо знать технологию производства, поставок, испытаний, условий эксплуатации. При этом от учета «тонких» костей зависит успех принятия решения.

Диаграммы ПАРЕТО

«Проблема организации общества должна решаться не декламациями вокруг более или менее смутного идеала справедливости, а только научными исследованиями, задача которых – найти способ соотношения средств с целью, а для каждого человека – усилий и страданий с наслаждением так, чтобы минимум страданий и усилий обеспечивал как можно большему числу людей максимум благосостояния» Вильфредо Парето

Метод Парето позволяет определить величину влияния фактора на причину в общей совокупности бесчисленных факторов, действующих на управляемую систему.

Схема, построенная на основе группировки событий (результатов) по дискретным признакам (причинам), ранжированная в порядке убывания (например, по частоте появления), и показывающая кумулятивную (накопленную) частоту, называется диаграммой распределения Парето.

В процессе управления при возникновении каких-либо трудностей важно выявить главные причины и разработать мероприятия для преодоления этих трудностей, ибо важно понять – с чего начинать действовать.

Для примера построим диаграмму Парето на основе группировки бракованной продукции по видам брака. На графике расположим эти группы в порядке убывания числа единиц бракованной продукции каждого вида:

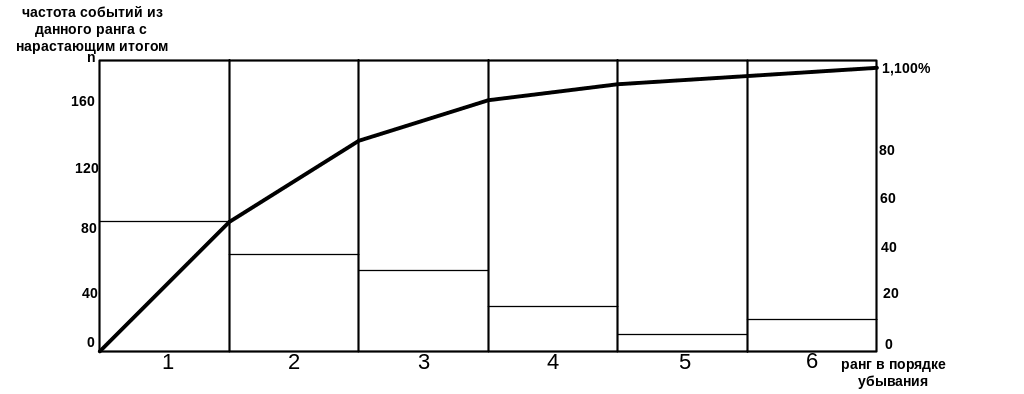
1. нарушения технологии производства

2. некачественное сырье

3. некачественные орудия труда

4. некачественные шаблоны

5. некачественные чертежи

6. прочие

l - относительная кумулятивная (накопленная) частота,%

n– число бракованных единиц продукции

В большинстве случаев преобладающая часть суммы убытков обусловлена небольшой частью факторов и если разработать мероприятия по их устранению, то получится наибольший эффект.

АВС – анализ применяется менеджерами для многих процессов управления, где требуется распределение усилий. Он основан на диаграмме Парето. В АВС-анализе используется двойное накопление до 100 процентов, как на оси абсцисс, так и на оси ординат.

Например, в случае управления запасами на складе менеджер реализует способ оптимального управления путем отслеживания периодов наибольшего скопления каждого из видов продукции, чтобы ранжировать в порядке убывания частоты использования каждого из видов продукции и объединить их в три группы А, В, С. Это позволит соответственно выстроить приоритеты в затратах и усилиях.

Нижеприведенный рисунок иллюстрирует метод АВС-анализа, где:

1. запасы постоянно используемых изделий (А – группа сильно меняющаяся),

2. запасы периодически используемых изделий (В – группа),

3. запасы редко используемых изделий (С – часть, слабо меняющаяся),

М – накопленные проценты по числу изделий,

N – накопленные проценты сумм поступлений со склада.

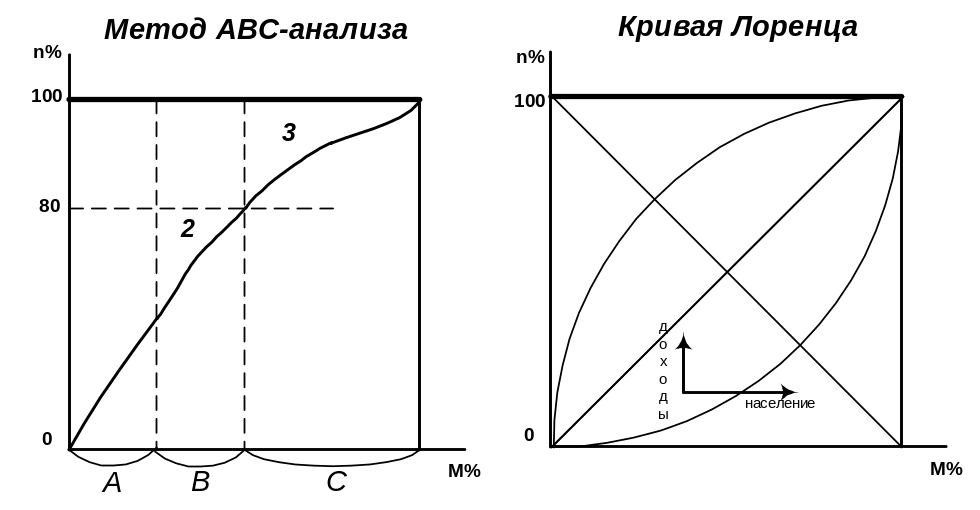
Кривая (диаграмма) Парето построена для накопления в убывающем порядке. Но если по тем же данным строить кривую для накопления в возрастающем порядке, получится симметричная диаграмме Парето кривая Лоренца. Она издавна используется в теории распределения доходов (10% населения имеет 90% доходов). Департамент экономики и прогнозирования рассчитывает децимальные коэффициенты для территорий и отраслей, в которых занято население: какую долю доходов имеют 10% самых богатых и 10% самых бедных людей в группе общества. Практически в любом государстве невозможно опротестовать тезис, что среди 80% населения распределена доля национального дохода всего в 20%.

Диагональ, проходящая через точки пересечения кривых 1 и 2, называется линией равновесия. Если разброс данных в пространстве «усилия – результат» по группам невелик, то кривая приближается к линии равновесия.

При АВС - анализе применяют разные подходы: можно при исследовании затрат взять за основу годовой объем сбыта по товарным позициям, или площадь, необходимую для хранения, или другие показатели.

Пример: на некоторой фирме работают 80 продавцов, а суммы продаж, обеспеченные ими распределяются согласно таблице:

Сумма продаж, руб./день	От 7 т. до 8 т.	6-7 - это класс	5-6 (центр класса =5,5)	4-5	3-4	2-3	1-2	0-1	Итого
Число продавцов	1	2	4	5	7	4	22	35	80

Составим таблицу накопленных процентов

Выручка, тыс.руб. (центр класса)	Число продавцов	Выручка		Число продавцов
		Накопленная сумма	Проценты	Накопленное число продавцов	Проценты
1	2	3	4	5	6
7,5	1	7,5 +	5,0	1	1,3
6,5	* 2	20,5	13,7	3	3,8
5,5	4	42,5	28,3	7	8,8
4,5	5	65,0	43,3	12	15,0
3,5	7	89,5	59,7	19	23,8
2,5	4	99,5	66,3	23	28,8
1,5	22	132,5	88,0	45	56,3
0,5	35	150,0	100,0	80	100,0

Таблица составляется в 3 этапа:

1. Подсчитывают сумму произведений для значений центров классов по выручке и числа продавцов.

Общая сумма = 7,5*1+6,5*2+…+0,5*35 = 150 тыс.рублей;

2. данные столбца (3) для второй строки = значение (1)*(2) из 1 стр. +(1)*(2) из 2 стр. = 7,5*1+6,5*2 = 20,5 и т.д.

Столбец (4) показывает, сколько процентов от общей суммы составляют данные каждой строки;

3. образуют данные столбца (6), например, значение 3,8 из 2 строки представляет собой количество процентов, приходящееся на накопленное число продавцов (1+2=3) от всего их числа 80.

4. После построения АВС - кривой можно сделать вывод, что продавцы, входящие в группу «А», являются для этой компании незаменимыми работниками.

Оценка влияния различных факторов на проблему.

Если СС разбита на группы по какому-либо признаку, то для оценки влияния различных факторов, определяющих колеблемость индивидуальных значений признака, можно воспользоваться разложением дисперсии на составляющие: на межгрупповую и внутригрупповую дисперсии.

Если рассчитать дисперсию по всей СС, т.е. общую дисперсию , то она будет характеризовать вариацию признака как результат влияния всех факторов, определяющих индивидуальные различия единиц СС.

Если поставить задачу - выделить в составе общей дисперсии ту ее часть, которая обусловлена влиянием какого-то определенного фактора, то следует разбить СС на группы, положив в основу группировки интересующий нас фактор.

Затем надо изучить раздельно вариацию признака внутри однородных в отношении данного фактора групп и изменения в величине признака от группы к группе.

Такая группировка позволяет разложить общую дисперсию признака на две дисперсии:

1. дисперсия, характеризующая часть вариации, обусловленную влиянием фактора, лежащего в основе группировки;

2. дисперсия, характеризующая часть вариации, происходящую под влиянием прочих факторов.

Отклонение индивидуальных значений признака от общей средней :

Метод дисперсионного анализа (ДА) был разработан Р.А.Фишером около 70 лет тому назад для решения вопросов, связанных с оценкой результатов сельскохозяйственного эксперимента. Метод позволяет количественно определить значимость и долю влияния различных факторов на результативный признак. Метод предполагает анализ небольших серий индивидуальных наблюдений, требует четкого планирования и организации эксперимента и весьма кропотливых расчетов.

ДА позволяет: измерять силу влияний, определять их достоверность, оценивать разности частных средних, изучать действие на конечный результат нескольких факторов вместе, роль каждого из них и сравнивать действие отдельных факторов между собой.

Основная идея ДА заключается в следующем. Если предположить, что исследуется действие нескольких факторов (Ф1, Ф2, Фj, …Фn) на определенный признак (Х) и что каждый фактор наблюдается m раз, то будет получено n*m наблюдаемых значений. При этом возможно из общей дисперсии всех наблюдаемых значений выделить дисперсию, являющуюся следствием влияния изучаемых факторов и дисперсию, являющуюся следствием влияния случайных причин, так называемую остаточную дисперсию – . Сравнивая и , можно с определенной степенью вероятности установить, насколько существенно влияние изучаемого фактора на величину признака. Дальнейшее изучение факторов проводят путем сравнения средних значений наблюдаемого признака, полученных в результате воздействия каждого из этих факторов в отдельности и при разном их сочетании.

Метод ДА может быть использован для изучения влияния различного числа факторов при одинаковом или неодинаковом числе наблюдений в отношении действия каждого из факторов. В связи с этим различают: однофакторный, двухфакторный и многофакторный (3 и более) дисперсионный анализ, а также равномерный и неравномерный комплексы.

Основные понятия ДА. В ДА принимаются следующие обозначения и названия.

Факторами принято называть любые воздействия или состояния, определяющие ту или иную величину наблюдаемого признака. Обозначаются они обычно заглавными буквами латинского алфавита – А,В,С и т.д. Наблюдаемые признаки, которые испытывают влияние изучаемых факторов, называются результативными . Отдельные же значения результативного признака именуются датами, вариантами .

Из многих факторов, влияющих на результативный признак, учету подлежит лишь небольшая группа основных, организованных в данном исследовании факторов . Учет влияния остальных (неконтролируемых) факторов ведется суммарно, не дифференцированно. Эти факторы называют случайными .

Из отдельных дат формируются специальные таблицы, называемые статистическим комплексом (СК). СК разделяются на:

1. равномерные – с одинаковым числом дат в каждой клетке комбинационной таблицы;

2. пропорциональные, в которых число дат в различных клетках комбинационной таблицы различно, но соблюдена единая для всего СК пропорциональность между ними;

3. непропорциональные, в которых распределение дат по клеткам таблицы различно.

Вариация изучаемого признака зависит как от организованных, так и от случайных факторов. Поэтому общая дисперсия слагается из дисперсии, вызванной организованными факторами – факторной дисперсии (межгрупповой)– и дисперсии, вызванной случайными факторами – остаточной дисперсии – :

Когда измеряется влияние нескольких факторов (в многофакторном комплексе – группировочной таблице), сумма дисперсий каждого из учитываемых факторов и случайной дисперсии должна быть равна общей дисперсии:

Доля участия отдельных факторов в формировании результативного признака определяется из отношения групповых дисперсий к общей (в процентах). Вычислив отношение факториальной дисперсии к общей , получаем долю влияния организованных факторов:

Точно так же вычисляется доля участия случайных факторов

При этом 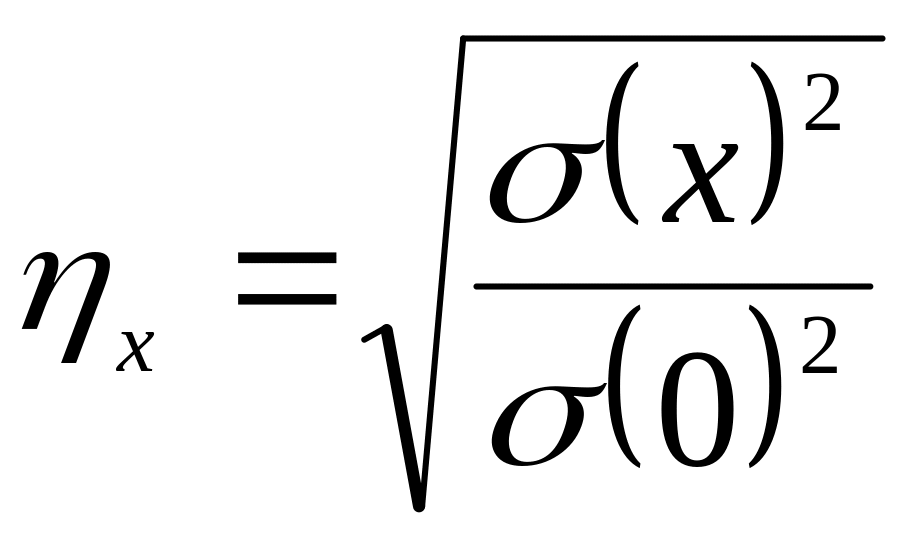– не что иное, как корреляционное отношение, обычный показатель криволинейной связи двух признаков.

Межгрупповая дисперсия (влияние группировочного фактора):

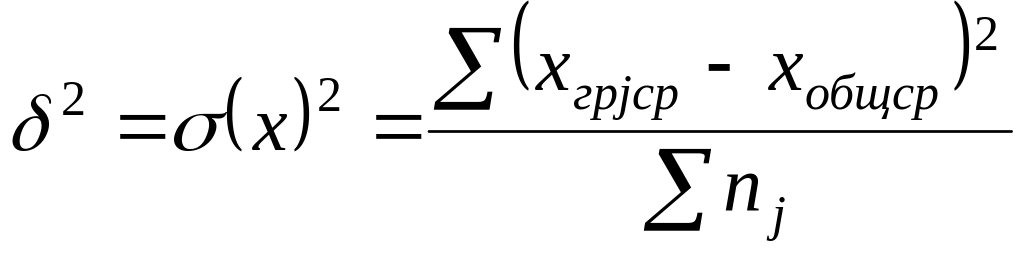, где nj – число единиц в j –й группе.

Внутригрупповая дисперсия характеризующая вариацию под влиянием прочих случайных факторов:

, а по совокупности в целом вариация значений признака под влиянием прочих факторов характеризуется средней из внутригрупповых дисперсий:

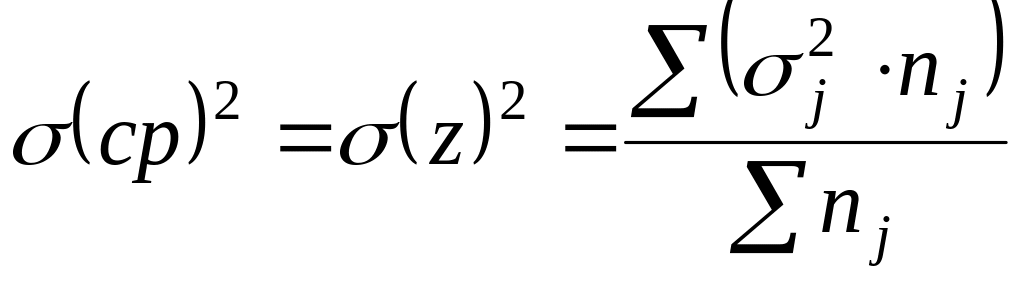
Между общей дисперсией , средней из внутригрупповых дисперсий и межгрупповой существует соотношение (правило сложения дисперсий):

Этот метод соответствует положениям теории Адольфа Кетле:

Массовые явления в исследуемой совокупности (ИС) формируются под влиянием 2-х групп причин:

1) определяющие состояние массового процесса, связаны с сущностью ИС, формируют типичный уровень для единиц качественно-однородной совокупности

2) индивидуальные случайные причины, не связанные с природой ИС, формируют специфические особенности отдельных единиц ИС

Рассмотрим пример влияния фактора обучения на производительность труда (ед.продукции / ед.времени):

1-бр. -необученные.				2-бр. –обученные специально
№ испыт.				№ испыт.
	(призв-ть)				(призв-ть)
1	13	-2	4	1	18	-3	9
2	14	-1	1	2	19	-2	4
3	15	0	0	3	22	1	1
4	17	2	4	4	20	-1	1
5	16	1	1	5	24	3	9
6	15	0	0	6	23	2	4
СУММА	90		10	СУММА	126		28