Свойства дисперсии

Дисперсия постоянной величины с равна нулю.

Доказательство: по определению дисперсии

При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не меняется.

D[X+c] = D[X].

Доказательство: по определению дисперсии

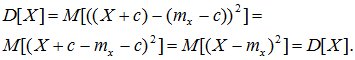(6.12)

3. При умножении случайной величины х на неслучайную величину с ее дисперсия умножается на с2.

Доказательство: по определению дисперсии

. (6.13)

Для среднего квадратичного отклонения это свойство имеет вид:

(6.14)

Действительно, при ½С½>1 величина сХ имеет возможные значения (по абсолютной величине), большие, чем величина Х. Следовательно, эти значения рассеяны вокруг математического ожидания М[сХ] больше, чем возможные значения Х вокруг М[X], т.е. . Если 0<½с½<1, то .

Правило 3s. Для большинства значений случайной величины абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, или, другими словами, практически все значения СВ находятся в интервале:

[ m - 3s; m + 3s; ].(6.15)

Билет 16. Теоремы сложения вероятностей

Несколько событий называются несовместимыми, если появление одного из них исключает возможность появления остальных.

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий

P (AÈB) =P (A) +P (B). (2.1)

Если имеется счетное множество несовместных событий A₁, ... , A_n, то

. (2.2)

Из правила сложения вероятностей вытекает, что если события A₁, A₂, …, A_n несовместны и образуют полную группу, то сумма их вероятностей равна единице; т.е. если

A_iּA_j=О при i≠j, то

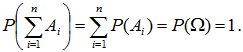(2.3)

В частности, если два события А и противоположны, то они образуют полную группу несовместных событий и

(2.4)

Тогда

(2.5)

Вероятность суммы двух совместных событий равна сумме вероятностей каждого из событий минус вероятность их совместного появления:

. ошибка-пересечение (2.6)

 

Билет 7. Основные определения. Случайные, достоверные и невозможные события

Теория вероятностей – математическая наука, изучающая закономерности в случайных явлениях. Одним из основных понятий теории вероятностей является понятие случайного события (или просто события).

Событием называется любой факт, который в результате опыта может произойти или не произойти. Примеры случайных событий: выпадение шестерки при подбрасывании игральной кости, отказ технического устройства, искажение сообщения при передаче его по каналу связи. С событиями связываются некоторые числа, характеризующие степень объективной возможности появления этих событий, называемые вероятностями событий.

К понятию «вероятность» существует несколько подходов.

Современное построение теории вероятностей основывается на аксиоматическом подходе и опирается на элементарные понятия теории множеств. Такой подход называется теоретико-множественным.

Пусть производится некоторый опыт со случайным исходом. Рассмотрим множество W всех возможных исходов опыта; каждый его элемент будем называть элементарным событием, а множество Ω – пространством элементарных событий. Любое событие A в теоретико-множественной трактовке есть некоторое подмножество множества Ω: .

Достоверным называется событие W, которое происходит в каждом опыте.

Невозможным называется событие Æ, которое в результате опыта произойти не может.

Несовместными называются события, которые в одном опыте не могут произойти одновременно.

Суммой (объединением) двух событий A и B (обозначается A+B, AÈB) называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно.

Произведением (пересечением) двух событий A и B (обозначается A×B, AÇB) называется такое событие, которое заключается в том, что происходят оба события A и B вместе.

Противоположным к событию A называется такое событие , которое заключается в том, что событие A не происходит.

События A_k (k=1, 2, ..., n) образуют полную группу, если они попарно несовместны и в сумме образуют достоверное событие.