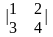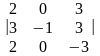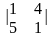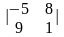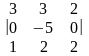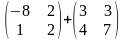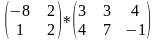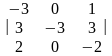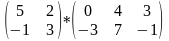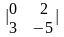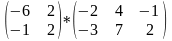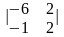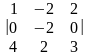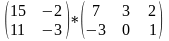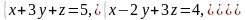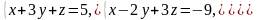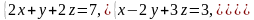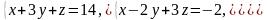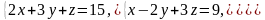1 Выполнение операций над матрицами. Вычисление определителей

Цель работы: научиться выполнять сложение, умножение матриц, вычисление определителей.

Ход работы:

(задания согласно вариантам)

1. Выполнить сложение матриц

2. Выполнить умножение матриц

3. Вычислить определитель матрицы второго порядка

4. Вычислить определитель матрицы третьего порядка

Пример ВЫПОЛНЕНия заданий

1. Выполнить сложение матриц

2. Выполнить умножение матриц

2. Вычислить определитель матрицы второго порядка

2. вычислить определитель матрицы третьего порядка разложением по первой строке, так как в первой строке содержится 0 (можно было разложить и по второму столбцу, так как в нем также содержится нулевой элемент)

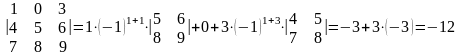
1 вариант 1) 1) 1) 1)	9 вариант 1) 2) 3) 4)
2 вариант 1) 2) 3) 4)	10 вариант 1) 2) 3) 4)
3 вариант 1) 2) 3) 4)	11 вариант 1) 2) 3) 4)
4 вариант 1) 2) 3) 4)	12 вариант 1) 2) 3) 4)
5 вариант 1) 2) 3) 4)	13 вариант 1) 2) 3) 4)
6 вариант 1) 2) 3) 4)	14 вариант 1) 2) 3) 4)
7 вариант 1) 2) 3) 4)	15 вариант 1) 2) 3) 4)
8 вариант 1) 2) 3) 4)

Контрольные вопросы:

1. Дайте определение матрицы, размерности матрицы, определителя и порядка определителя. Приведите примеры.

2. Дайте определение квадратной матрицы, диагональной матрицы, ступенчатой матрицы, единичной матрицы.

3. Дайте определение алгебраического элемента матрицы. Приведите формулу для вычисления алгебраического дополнения.

4. Перечислите возможные действия над матрицами.

5. Назовите способы вычисления определителя третьего порядка.

2 Решение систем линейных уравнений

Цель работы: научиться решать системы линейных уравнений методами Крамера и Гаусса.

Ход работы:

(согласно вариантам)

1. Решить систему линейных уравнений методом Крамера

2. Решить систему линейных уравнений методом Гаусса

Пример ВЫПОЛНЕНия заданий

Найти решение системы линейных уравнений методом Гаусса и методом Крамера.

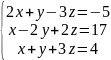
Решим СЛУ методом Крамера:

Найдем основной определитель, составленный из коэффициентов при x, y, z:

Чтобы найти , , , 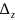Заменяем в основном определителе соответствующие столбцы на столбец свободных членов (для х первый столбец, для у второй столбец, для z третий столбец):

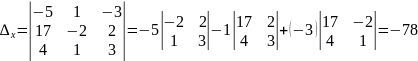
Найдем решение системы по формулам Крамера:

Решим СЛУ методом Гаусса. Для этого почленно умножаем каждое уравнение системы на необходимый коэффициент и складываем попарно уравнения:

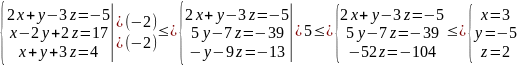
1 вариант №1. №2.	4 вариант №1. №2.
2 вариант №1. №2.	5 вариант №1. №2.
3 вариант №1. №2.	6 вариант №1 №2.
7 вариант №1. №2.	12 вариант №1. №2.
8 вариант №1. №2.	13 вариант №1. №2.
9 вариант №1. №2.	14 вариант №1. №2.
10 вариант №1. №2.	15 вариант №1. №2.
11 вариант №1. №2.

Контрольные вопросы:

1. Запишите формулы Крамера.

2. В чем заключается метод Гаусса?

3. Назовите способы вычисления определитель третьего порядка.