23. Агрегатные общие индексы.

О бъективность общим индексам придает их запись в агрегатном виде, предложенная испанцем Ласпейресом и немцем Пааше.

Агрегатный общий индекс Ласпейреса для количества товаров как первого фактора выручки определяется по формуле

Аналогично можно записать агрегатный общий индекс Ласпейреса для цен как первого фактора выручки, то есть

В формулах Ласпейреса знаменатели по существу одинаковые, представляя собой выручку базисного периода, а числители разные. В формуле это отчетная выручка в базисных ценах (количесгво товаров отчетное, а цены — базисные), в формуле наоборот — базисная выручка в отчетных ценах (цены отчетные, а количество товаров — базисное).

А грегатные общие индексы Пааше применяются ко вторым факторам мультипликативных моделей. Поэтому такой индекс для цен как второго фактора выручки определяется по формуле

Аналогично можно записать агрегатный общий индекс Пааше для количества товаров как второго фактора выручки, то есть

В формулах Пааше числители по существу одинаковые, представляя собой выручку отчетного периода, а знаменатели аналогичны числителям формул Ласпейреса.

Н о в статистике должно быть одно значение индекса, поэтому американский экономист Фишер предложил применять среднюю геометрическую величину из индексов Ласпейреса и Пааше, определяя ее по формулам:

д ля количества товаров и для цен

Вместе с тем, проведенные Ворониным В.Ф. многочисленные расчеты показали, что для целей статистики вполне можно применять не среднюю геометрическую, а простую среднюю арифметическую величину из

индексов Ласпейреса и Пааше, определяя ее по формулам:

для количества товаров и для цен -

24. Общие индексы как средние из индивидуальных индексов.

Помимо записи общих индексов в агрегатном виде, на практике часто используют формулы их расчета как величин, средних из соответствующих индивидуальных индексов.

И спользуя их формулы, можем записывать, что q1 = q0iq и p1 = p0ip, а также, что q0 =q1/iq и р0=р1/ip. Подставив отчетные значения количества товара и цены в формулу общего индекса выручки, получим IQ===Значит, общий индекс выручки можно определять только через ее базисные значения с умножением в числителе на индивидуальный индекс выручки по конкретному товару.

Т еперь подставим базисные значения количества товара и цены в формулу общего индекса выручки. Тогда получим Значит, общий индекс выручки можно определять только через ее отчетные значения с делением в знаменателе на индивидуальный индекс выручки по конкретному товару.

Аналогично через индивидуальные индексы количества товара и цены можно выразить агрегатные общие индексы Ласпейреса и Пааше

25. Индексы средних величин: индексы постоянного и переменного состава, индексы структурных сдвигов.

Изменение средней величины показателя зависит от двух факторов – изменения значения индексируемого показателя у отдельных единиц и изменения структуры явления.

И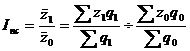 зменение структуры – это изменение доли отдельных групп единиц совокупности в общей их численности. Задача определения влияния каждого фактора определяется с помощью индексного метода, т.е. путем построения системы взаимосвязанных индексов, в которую включаются три индекса: переменного состава, постоянного состава и структурных сдвигов.

Индекс переменного состава – индекс, выражающий соотношение средних уровней изучаемого явления, относящихся в разным периодам времени. Например, индекс переменного состава себестоимости продукции:

Отражает изменение не только изменение индексируемой величины (в данном случае, себестоимости), но и структуры совокупности весов (объем).

И ндекс постоянного состава – это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Например, индекс фиксированного состава себестоимости продукции:

И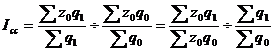 ндекс структурных сдвигов – индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления:

Система взаимосвязанных индексов при анализе динамики средней себестоимости имеет следующий вид: