7.Какое утверждение выполняется с большей степенью точности? Ускорение свободного падения :

1) одинаково во всех точках поверхности Земли;

2) в каждой точке поверхности Земли одинаково для тел

различной массы;

3) одинаково для тел, имеющих одинаковую массу в разных

точках поверхности Земли;

4) одинаково на поверхности всех планет Солнечной системы.

8. Потенциальная энергия спутника массой , вращающегося по орбите радиуса , на высоте H вокруг Земли, в общем случае равна:

1) , 2) , 3) , 4)

9. Если в поднимающемся вверх с ускорением лифте находится тело массой , то вес этого тела будет:

1) , 2) , 3) , 4) .

10. Лифт двигается вверх и в какой-то момент начинает тормозить с ускорением . Вес находящегося в лифте человека, масса которого будет в этот момент равен:

1) , 2) , 3) , 4) .

11. Лифт движется вниз и в какой-то момент начинает тормозить с ускорением . В этот момент вес находящегося в лифте человека массой станет равным:

1) , 2) , 3) , 4) .

12. Силы инерции необходимо учитывать при решении задач:

1) о движении с ускорением в любой системе отсчета (СО);

2) о любом движении в неинерциальной системе отсчета;

3) только о вращательном движении в любой системе отсчета;

4) только для покоящегося тела во вращающейся СО.

13. Силы инерции нужно учитывать всегда:

1) когда тело движется с ускорением;

2) когда решаем задачу в инерциальной СО;

3) когда решаем задачу в неинерциальной СО;

4) когда тело движется равномерно и прямолинейно.

14. Центробежную силу нужно учитывать всегда, когда:

1) когда тело движется по окружности;

2) когда решаем задачу во вращающейся системе отсчета;

3) когда вращение происходит в инерциальной системе отсчета;

4) когда тело двигается по поверхности цилиндра.

15. Центробежная сила, действующая на пассажира массой , находящегося в автомобиле, совершающем поворот радиусом при скорости равна:

1) ; 2) ; 3) ; 4) .

16. Центробежная сила действующая на человека, находящегося на платформе, которая вращается с угловой скоростью равна ( - расстояние от оси вращения до человека):

1) , 2) , 3) ; 4) .

17. Сила Кориолиса равна ( - масса, - угловая скорость, - поступательная скорость в НеИСО, - угловое ускорение):

1) , 2) , 3) , 4) .

18. Благодаря вращению Земли и действию силы Кориолиса реки сильнее подмывают:

1) восточный берег;

2) западный берег;

3) западный или восточный в зависимости от направления течения реки;

4)западный весной, а восточный осенью.

19. Если по платформе, вращающейся с угловой скоростью , катится шарик со скоростью , то действующая на шарик сила Кориолиса:

1) параллельна ;

2) параллельна ;

3) перпендикулярна ;

4) перпендикулярна векторному произведению .

20. Благодаря эквивалентности масс, по измерениям, проведенным в рамках одной системы отсчета (СО) невозможно отличить

1) одну инерциальную СО от другогй

2) инерциальную СО, находящуюся в гравитационном поле от другой инерциальной СО, в которой поле отсутствует

3) неинерциальную СО от инерциальной, находящейся в гравитационном поле.

4 ) одну неинерциальную СО от другой, движущейся с другим ускорением.

21. Принцип эквивалентности масс провозглашает эквивалентность

1. массы покоя и релятивистской массы;

2. массы, движущейся по инерции, и массы, движущейся с ускорением

3) массы у поверхности Земли и массы поднятой над Землей на некоторую высоту

4) гравитационной массы и инерционной массы.

22. Первая космическая скорость – это скорость,

    1. которую достигла первая, запущенная в СССР ракета;

    2. которую сообщает спутнику первая ступень ракеты;

    3. которая позволяет спутнику выйти на околоземную орбиту;

    4. которая позволяет осуществить межпланетные перелеты.

22. Вторая космическая скорость – это скорость,

1) которую сообщает космическому кораблю вторая ступень

ракеты;

2) которая позволяет ракете выйти из сферы земного притяжения;

3) необходимая для межзвездных путешествий (субсветовая

скорость)

4) спутника на орбите.

5. Колебания и волны.

1.На пружине подвешен груз, масса которого . Если к грузу прикрепить дополнительно гирьку такой же массы, то собственная частота системы:

1. увеличится в 2 раза;

2. увеличится в 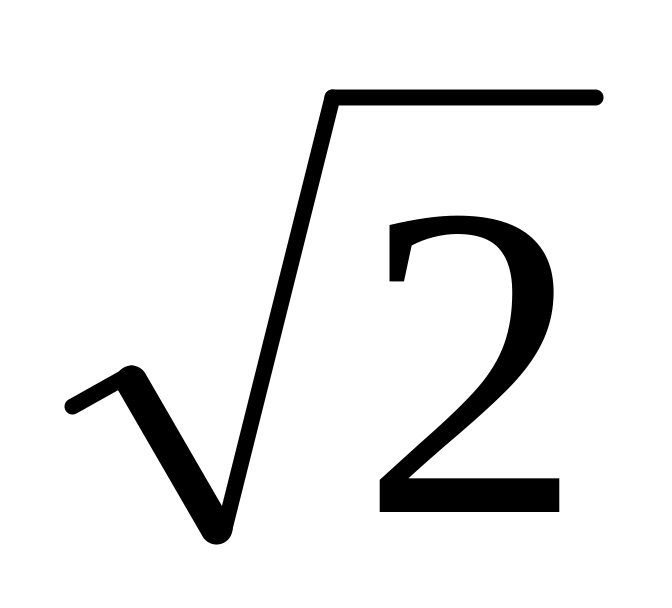раз;

3. уменьшится в раз;

4. уменьшиться в 2 раза.

2. Тело, масса которого колеблется под действием силы ( в см, в Ньютонах). Собственная циклическая частота системы равна:

1) ; 2) ; 3) ; 4) .

3. При увеличении амплитуды колебаний груза на пружине в 2 раза, период колебаний:

1) уменьшиться в 2раза;

2) уменьшиться в раз;

3) не изменится;

4) увеличиться в раз.

4. Собственные колебания механической системы будут гармоническими, если возвращающая сила:

1) постоянна;

2) пропорциональна смещению из положения равновесия;

3) пропорциональна квадрату смещения

4) пропорциональна косинусу ( или синусу) смещения.

5. Колебания происходят по гармоническому закону, если потенциальная энергия колеблющегося тела U зависит от смещения x из положения равновесия следующим образом:

1) ; 2 ) ; 3) ; 4) .

6. Фаза колебаний измеряется:

1) в метрах;

2) в секундах;

3) в радианах;

4) в герцах.

7. Период малых колебаний математического маятника равен:

1) ; 2) ; 3) ; 4) .

8. Период малых колебаний физического маятника, имеющего массу m и момент инерции относительно оси вращения J ( - расстояние от оси до центра масс) равен:

1) ; 2) ; ; .

9. Собственная частота ω₀ малых колебаний математического маятника, имеющего массу m, длину l (g- ускорение свободного падения) равна:

1) ; 2) ; 3) ; 4) .

10. Собственная частота ω₀ малых колебаний физического маятника имеющего массу m, момент инерции J, у которого расстояние от оси до центра массы , равна:

1) ; 2) ; 3) ; 4) .

11. Если частота звучания двух струн отличается на 16 Гц, то период изменения громкости их совместного звучания будет равен:

1) ; 2) ; 3) ; 4) .

12. Период малых колебаний математического маятника равен . Если его поместить в лифт, опускающийся с ускорением (направленным вниз) , то колебания будут происходить с частотой:

1) ; 2) ; 3) ; 4) .

13. Период малых колебаний математического маятника равен . Если маятник поднимают вверх с ускорением , то его колебания будут происходить с частотой:

1) ; 2) ; 3) ; 4) .

14. При сложении двух колебаний с одинаковыми частотами, начальные фазы которых и амплитуда результирующего колебания а связана с амплитудами каждого из колебаний ( и ) соотношением:

1) ; 2) ;

3) ; 4) .

15. Если периодический процесс имеет негармонический характер, то его можно представить:

1) как сумму гармонических колебаний с кратными частотами;

2) как сумму гармонических колебаний с близкими частотами;

3) как сумму колебаний с одной частотой, имеющих различные начальные фазы;

16. Биения возникают:

А) при сложении колебаний с близкими частотами;

В) при сложении колебаний с кратными частотами.

Биения представляют собой:

С) короткие импульсы колебаний, перемежающиеся паузами без колебаний,

D) гармонические колебания с периодически меняющейся амплитудой.

Правильными являются утверждения:

1) АС; 2) АD; 3)ВС; 4) BD.