
- •Донецк-2001
- •Донецк-2001
- •1Введение в теорию множеств
- •1.1Основные определения
- •1.2Способы задания множества
- •1.3Операции над множествами
- •1.4Основные законы алгебры множеств
- •1.5Контрольные вопросы
- •2Отношения на множествах
- •2.1Теоретические сведения
- •2.2Способы задания отношений
- •2.3Свойства бинарных отношений
- •2.4Функциональные отношения
- •2.5Контрольные вопросы
- •3Основные понятия комбинаторики.
- •3.1Правила суммы и произведения
- •3.1.1Правила суммы
- •3.1.2Правило произведения
- •3.1.3Сложный выбор объектов
- •3.2Соединения без повторений
- •3.2.1Перестановки
- •3.2.2Размещения
- •3.2.3Сочетания
- •3.2.4Свойства сочетаний
- •3.3Соединения с повторениями
- •3.3.1Перестановки с повторениями
- •3.3.2Размещения с повторениями.
- •3.3.3Сочетания с повторениями.
- •3.4Контрольные вопросы
- •4Булева алгебра
- •4.1Определение функции алгебры логики
- •4.2Способы описания фал
- •4.2.1Табличный способ представления фал
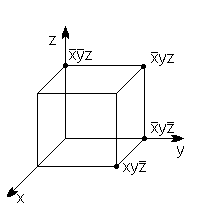
- •4.2.2Графическое представление фал
- •4.3Функции алгебры логики одного аргумента
- •4.4Функции алгебры логики двух аргументов
- •4.5Условные приоритеты булевых функций
- •4.6Фиктивные аргументы фал
- •4.6.1Алгоритм нахождения фиктивных аргументов
- •4.8Выражение одних элементарных функций через другие
- •4.9Аналитическая запись фал
- •4.9.1Дизъюнктивная нормальная форма (днф)
- •4.10Полные системы фал
- •4.11Контрольные вопросы
- •5Методы минимизации функций алгебры логики.
- •5.1Основные определения
- •5.2Минимизация фал на кубе
- •Пункты решения задачи по минимизации
- •Четырехмерное пространство
- •5.3Метод Квайна
- •5.4Метод Мак-Класки
- •5.5Графический метод минимизации: карты Карно и диаграммы Вейча
- •5.6Основные принципы построения карт Карно
- •5.7Контрольные вопросы
- •6Контрольные работы для студентов заочного отделения.
- •6.1Контрольная работа № 1.
- •6.2Контрольная работа № 2.
- •6.3Алгоритм генерации варианта
- •7Примеры решения типовых зданий.
- •7.1Контрольная работа №1.
- •7.2Контрольная работа №2.
- •1 Введение в теорию множеств 3
- •2 Отношения на множествах 10
- •3 Основные понятия комбинаторики. 15
- •4 Булева алгебра 23
- •5 Методы минимизации функций алгебры логики. 36
- •6 Контрольные работы для студентов заочного отделения. 46
- •7 Примеры решения типовых зданий. 58
7.2Контрольная работа №2.
Задание 10.Функции Алгебры логики.
![]()
1 3 2 7 4 5 6
1,2…7 – последовательность выполнения действий.
x |
y |
z |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
Проверка фиктивности аргументов.




 000
000 000
000
000 000
100 100 100
101 0 101 0 101 0
 111
111 111
111
111 111
001 001 001
010 010 010
011 1 011 1 011 1
110 110 110
Фиктивных аргументов нет.
Задание 11.
Представить фал аналитически в ДСНФ и КСНФ.
ДСНФ:
![]()
КСНФ:
![]()
Задание 12.
Представить функцию в базисе штрих Шеффера и стрелка Пирса.
Штрих Шеффера
a. ДСНФ
![]()
1.
![]()
2.
![]()
![]()
![]()
КСНФ
![]()

Стрелка Пирса.
ДСНФ
![]()
![]()
![]()
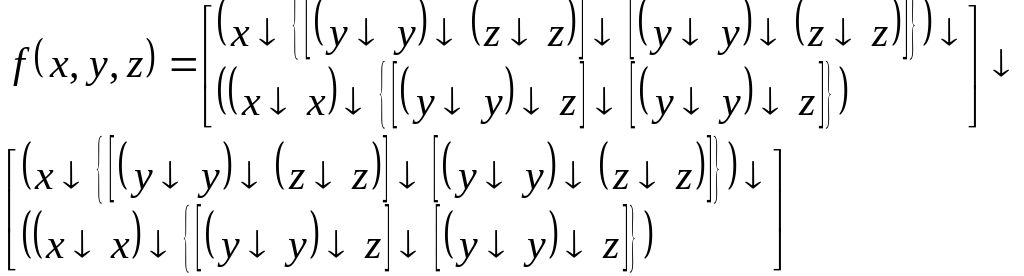
КСНФ

![]()
![]()
![]()
Задание 12.
Разложить ДСНФ по базису “и, не”,”или, не”.
Сравнить ”и, не” и , ”или, не” и /.

![]()
Задание 13.
А б в г д е ë ж з и й к л м н о п р с т у ф х ц ч ш щ ь ы ъ
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
э ю я
31 32 33
Ш и р к о в а е т н л с
26 10 18 12 16 3 1 6 20 15 13 19
Mod 16 10 10 2 12 0 3 1
Mod 32 26 10 18 12 16 3 1 6 20 15 13
f2 − 10, 2, 12, 0, 3, 1, 6;
f3 − 26, 10, 18, 12, 16, 3, 1, 6, 20, 15, 13;
f4 − 26, 10, 18, 12, 16, 3 – единичные наборы.
− 1, 6, 20, 15, 13 – неизвестные наборы
Задание 14.
![]() − минимальная
ДНФ.
− минимальная
ДНФ.
Ч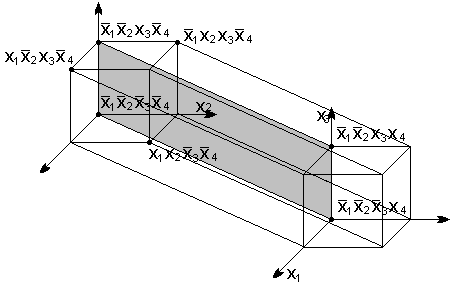 асть
2.
асть
2.
![]()
Метод Квайна-МакКласки.
|
X1 |
X2 |
X3 |
X4 |
f |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
2 |
0 |
0 |
1 |
0 |
1 |
3 |
0 |
0 |
1 |
1 |
1 |
4 |
0 |
1 |
0 |
0 |
0 |
5 |
0 |
1 |
0 |
1 |
0 |
6 |
0 |
1 |
1 |
0 |
1 |
7 |
0 |
1 |
1 |
1 |
0 |
8 |
1 |
0 |
0 |
0 |
0 |
9 |
1 |
0 |
0 |
1 |
0 |
10 |
1 |
0 |
1 |
0 |
1 |
11 |
1 |
0 |
1 |
1 |
0 |
12 |
1 |
1 |
0 |
0 |
1 |
13 |
1 |
1 |
0 |
1 |
0 |
14 |
1 |
1 |
1 |
0 |
0 |
15 |
1 |
1 |
1 |
1 |
0 |
1.Находим первичные импликанты:
x1 x2 x3 x4 |
x1 x2 x3 |
x1 x2 |
x1 x2 x3 x4 |
x1 x2 x3 |
|
x1 x2 x3 x4 |
x1 x2 x4 |
|
x1 x2 x3 x4 |
x1 x2 x4 |
|
x1 x2 x3 x4 |
x1 x3 x4 |
|
x1 x2 x3 x4 |
x2 x3 x4 |
|
x1 x2 x3 x4 |
|
|
2. Расставляем метки.
|
x1 x2 x3 x4 |
x1 x2 x3 x4 |
x1 x2 x3 x4 |
x1 x2 x3 x4 |
x1 x2 x3 x4 |
x1 x2 x3 x4 |
x1 x2 x3 x4 |
|
|
|
|
|
|
|
|
x1 x3 x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Все импликанты существенны.
Метод карт Карно.
|
00 |
01 |
11 |
10 |
|
1 |
1 |
1 |
1 |
01 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
0 |
10 |
0 |
0 |
0 |
1 |
Задание 15.
f3 − 26, 10, 18, 12, 16, 3, 1, 6, 20, 15, 13;
|
X1 |
X2 |
X3 |
X4 |
X5 |
F |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
2 |
0 |
0 |
0 |
1 |
0 |
0 |
3 |
0 |
0 |
0 |
1 |
1 |
1 |
4 |
0 |
0 |
1 |
0 |
0 |
0 |
5 |
0 |
0 |
1 |
0 |
1 |
0 |
6 |
0 |
0 |
1 |
1 |
0 |
1 |
7 |
0 |
0 |
1 |
1 |
1 |
0 |
8 |
0 |
1 |
0 |
0 |
0 |
0 |
9 |
0 |
1 |
0 |
0 |
1 |
0 |
10 |
0 |
1 |
0 |
1 |
0 |
1 |
11 |
0 |
1 |
0 |
1 |
1 |
0 |
12 |
0 |
1 |
1 |
0 |
0 |
1 |
13 |
0 |
1 |
1 |
0 |
1 |
1 |
14 |
0 |
1 |
1 |
1 |
0 |
0 |
15 |
0 |
1 |
1 |
1 |
1 |
1 |
16 |
1 |
0 |
0 |
0 |
0 |
1 |
17 |
1 |
0 |
0 |
0 |
1 |
0 |
18 |
1 |
0 |
0 |
1 |
0 |
1 |
19 |
1 |
0 |
0 |
1 |
1 |
0 |
20 |
1 |
0 |
1 |
0 |
0 |
1 |
21 |
1 |
0 |
1 |
0 |
1 |
0 |
22 |
1 |
0 |
1 |
1 |
0 |
0 |
23 |
1 |
0 |
1 |
1 |
1 |
0 |
24 |
1 |
1 |
0 |
0 |
0 |
0 |
25 |
1 |
1 |
0 |
0 |
1 |
0 |
26 |
1 |
1 |
0 |
1 |
0 |
1 |
27 |
1 |
1 |
0 |
1 |
1 |
0 |
28 |
1 |
1 |
1 |
0 |
0 |
0 |
29 |
1 |
1 |
1 |
0 |
1 |
0 |
30 |
1 |
1 |
1 |
1 |
0 |
0 |
31 |
1 |
1 |
1 |
1 |
1 |
0 |
Метод Квайна – МакКласки.
1. Находим первичные импликанты.
1 |
x1 x2 x3 x4 x5 |
x1 x2 x3 x5 (1 – 2) |
2 |
x1 x2 x3 x4 x5 |
x2 x3 x4 x5 (4 – 11) |
3 |
x1 x2 x3 x4 x5 |
x1 x2 x3 x4 (5 – 6) |
4 |
x1 x2 x3 x4 x5 |
x1 x2 x3 x5 (6 – 7) |
5 |
x1 x2 x3 x4 x5 |
x1 x2 x3 x5 (8 – 9) |
6 |
x1 x2 x3 x4 x5 |
x1 x2 x4 x5 (8 – 10) |
7 |
x1 x2 x3 x4 x5 |
x1 x3 x4 x5 (9 − 11) |
8 |
x1 x2 x3 x4 x5 |
|
9 |
x1 x2 x3 x4 x5 |
|
10 |
x1 x2 x3 x4 x5 |
|
11 |
x1 x2 x3 x4 x5 |
|
– существенная импликанта.
2. Расставляем метки.
|
1 |
2 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
x1x2 x3 x4 x5 |
x1x2 x3 x4 x5 |
x1 x2 x3 x4 x5 |
x1 x2 x3 x4 x5 |
x1 x2 x3 x4 x5 |
x1 x2 x3 x4 x5 |
x1x2 x3 x4 x5 |
x1x2 x3 x4 x5 |
x1x2 x3 x4 x5 |
x1 x2 x3 x4 x5 |
|
|
|
|
|
|
|
|
|
|
|
|
x2 x3 x4 x5 |
|
|
|
|
|
|
|
|
|
|
x1 x2 x3 x4 |
|
|
|
|
|
|
|
|
|
|
x1 x2 x3 x5 |
|
|
|
|
|
|
|
|
|
|
x1 x2 x3 x5 |
|
|
|
|
|
|
|
|
|
|
x1 x2 x4 x5 |
|
|
|
|
|
|
|
|
|
|
x1 x3 x4 x5 |
|
|
|
|
|
|
|
|
|
|
В ычеркиваем
столбцы, в которых только одна метка
ычеркиваем
столбцы, в которых только одна метка
В ычеркиваем
все строки, которые покрыли эти импликанты
ычеркиваем
все строки, которые покрыли эти импликанты
С толбцы
6, 8 и 11 покрыты, вычеркиваем их
толбцы
6, 8 и 11 покрыты, вычеркиваем их
Непокрыт только 9 столбец. Необходимо взять x1x2x3x5 или
x1x3 x4x5
![]()
![]() Метод
карт Карно.
Метод
карт Карно.
|
000 |
001 |
011 |
010 |
110 |
111 |
101 |
100 |
|
|
1 |
1 |
|
1 |
|
|
|
|
|
|
|
1 |
|
1 |
1 |
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
М
 ы
можем выбрать один из двух вариантов:
ы
можем выбрать один из двух вариантов:
Задание 16.
Метод карт Карно
x3,x4,x5,x1,x2 |
000 |
001 |
011 |
010 |
110 |
111 |
101 |
100 |
00 |
|
|
1 |
|
|
|
|
|
01 |
|
|
|
1 |
|
|
|
1 |
11 |
|
|
|
1 |
|
|
|
|
10 |
1 |
|
|
1 |
|
|
|
|
![]()
СОДЕРЖАНИЕ


 x1
x2
x1
x2 x2
x3
x4
x2
x3
x4 x1
x2
x3
x4
x1
x2
x3
x4


 00
00 11
11



 x1
x2
x3
x5
x1
x2
x3
x5
 x3,x4,x5,x1,x2
x3,x4,x5,x1,x2
 00
00 01
01 11
11 10
10