Література:

1. Програма з математики для загальноосвітніх навчальних закладів, 5 – 11 кл. // Математика в шк. – 2003.

2. Програми факультативів та курсів за вибором з математики для загальноосвітніх навчальних закладів 7 – 11 кл. – К.: Навч. кн., 2002.

3. Програма поглибленого вивчення математики в 10 – 11 профільних класах // Математика в шк. – 2003.

Тема: Функції в курсі алгебри і початків аналізу.

1. Введення поняття тригонометричних функцій числового аргументу.

2. Вивчення показникової функції.

3. Вивчення логарифмічної функції.

4. Степенева функція.

Введення поняття тригонометричних функцій числового аргументу.

Насамперед треба згадати означення тригонометричних функцій кута і поширити їх на функцій числового будь-яку градусну міру, ввести кут повороту.

Крім того, слід переконати учнів у тому, що іс­нує відповідність між множиною дійсних чисел і множиною точок одиничного кола

Означення І. Синусом числа а називається ордината точки Ра одиничного кола, в яку переходить початкова точка Ро (1; 0) при повороті навколо центра кола на кут а радіанів, і позначається sіп а.

Означення 2. Косинусом числа а називається абсциса точки Ра одиничного кола, в яку переходить початкова точка Ро (1; 0) при повороті навколо центра кола на кут а радіанів, і познача­ється соs а.

Означення 3. Тангенсом числа а називається відношення , а котангенсом числа - відношення і позначаються відповідно tg , ctg .

Оскілки кожному дійсному числу х можна поставити у відповідність дійсні числа sin x i cos x, то вважатимемо, що на множині R задано функції y=sin x, y=cos x.Враховуючи, що y=tg x= визначений для всіх х, крім тих, за яких cos x=0, і кожному дійсному числу, крім x= , n , відповідає єдине число tg x, вважатимемо, що y=tg x – функція, областю визначення якої є всі дійсні числа, крім х= , де п Z.

Доцільно виділити сім властивостей тригонометричних функцій і систематизувати їх так, як буде показано для функції y = sin х.

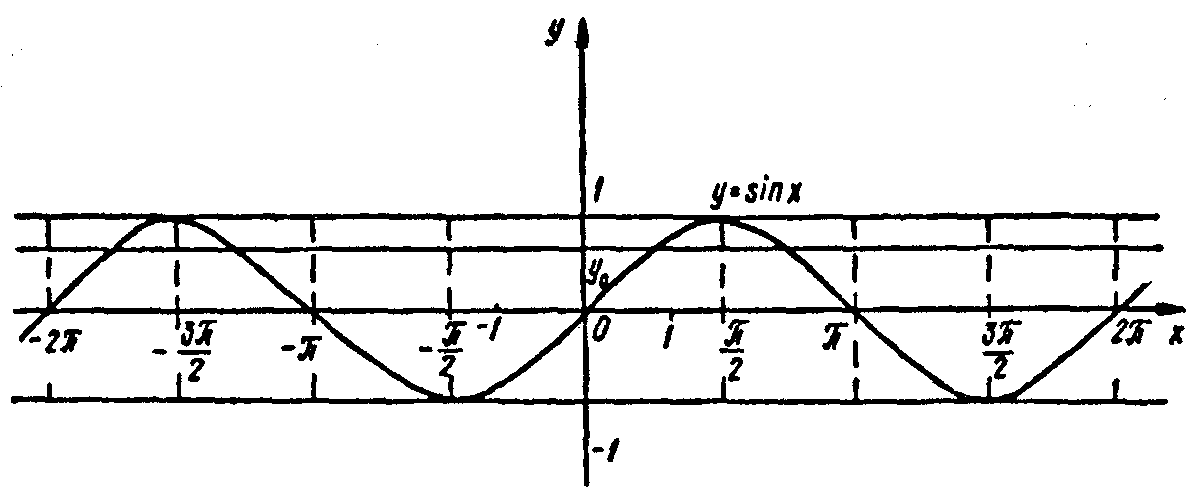
1. Оскільки синус існує для будь-якого дійсного числа і як ор­дината точки одиничного кола змінюється на відрізку від -1 до 1, то областю визначення функції y = sin х є множина R всіх дійсних чисел, а областю значень - відрізок

[-1; І].

2. Графік функції симетричний відносно початку координат, тобто функція y = sin х непарна. Доведемо це, користуючись оди­ничним колом.

Область визначення цієї функції - множина, симетрична щодо початку координат. Залишається довести, що sin(-а)=-sinа. Позначимо на одиничному колі точки Р і Р , які відповідають числам і - , що належать множині R. Оскільки пря­мокутні трикутники Р ОА і Р ОА рівні, то Р А = Р А (ОА - cпільний катет). Отже, абсциси точок Р і Р рівні, а ординати - протилежні числа. Тому sin (- ) = - sin .

3. Функція періодична з найменшим додатним періодом 2 .

4. Функція набуває значення, що дорівнює 0 (нулі функції) при х = k , де k Z, оскільки ординати точок одиничного кола перетворюються на нуль на відрізку [0, 2 у двох точках = і , а функція періодична.

5. Проміжки зростання функції - відрізки , де n Z.

6. Проміжками, де синус додатний, є (2п ; + 2п ), n Z, оскільки на відрізку [0; 2 ], довжина якого дорівнює найменшо­му додатному, періоду 2 , функція додатна на проміжку (0; ). Синус від'ємний на проміжках ( + 2п ; 2 + 2п ), оскільки на відрізку [0; 2 ] він від'ємний на проміжку ( ; 2 ).

7. Синус досягає максимуму, що дорівнює 1 в точках + 2 п, де n Z, а мінімуму, що дорівнює -1, у точках + 2 п, де n Z.

Вивчення показникової функції

Введення поняття показникової функції доцільно здійснювати за тією самою методичною схемою, за якою вивчалися всі попередні функції .

На етапі мотивації доцільно навести приклади залежностей, які виражаються через показникову функцію.

Приклад. Кількість мешканців міста з мільйонним населенням через .(років обчислюється за умови, що кожного року спостерігається приріст населення на 2 % за формулою y = 1 000 000 • 0,02^x.

Означення. Показниковою функцією називається функція у=a^х, де а - задане додатне число, не рівне одиниці, х і у – змінні.

Властивості функції учні спочатку «читають» за графіком, а відтак учитель доводить їх аналітичне. Попередньо треба повто­рити властивості степенів.

Властивість 1. Областю визначення функції у=а^х є множина всіх дійсних чисел, оскільки вираз а^х за а > 0 визначений для будь-якого х.

Властивість 2. Показникова функція набуває лише додатних значень.

Властивість 3. Якщо а>1, то за х>0 а^х>1, за х<0 0 < а^х <1. Якщо а <1, то, навпаки, за х > 0 0< а^х < 1, а за х < 0 а^х>1.

Властивість 4. Якщо х = 0, то при будь-якому а>0 у=а^х=1, що випливає з означення степеня з нульовим показником.

Властивість 5. Показникова функція при а > 1 зростаюча, а при 0 < а < 1 - спадна.

Властивість 6. Якщо а > 1, то за х + значення y + , а при х - значення у 0, залишаючись додатним. Враховую­чи монотонність функції, можна стверджувати, що в цьому випа­дку функція монотонне зростає від 0 до + .

Якщо 0<а<1,то за х + значення у 0, залишаючись додатними, а за х- значення у . Враховуючи моно­тонність, можна стверджувати, що в цьому випадку у = а^х монотонно спадає від + до 0.

Властивість 7. Областю значень функції є множина всіх до­датних чисел.

Вивчення логарифмічної функції

Перш ніж вводити логарифмічну функцію як функцію, обернену до показникової, доцільно ввести означення логарифма числа в за основою а (а>0, а 1) як показника степеня, до якого треба піднести число а, щоб дістати число в, і запрова­дити символ log_ab. Треба звернути увагу учнів на те, що лога­рифмічна рівність log_ab=х і показникова а^x=b виражають те саме співвідношення між числами а,b і х. За цими рівностями можна знайти одне з трьох чисел, яке до них входить.

Можна запропонувати учням самостійно знайти функцію, обернену до показникової функції y=a^х, скориставшись відомим їм алгоритмом відшукання формули функції, оберненої до даної, з яким вони могли ознайомитися раніше під час вивчення обер­нених тригонометричних функцій. Учні самі доходять означення логарифмічної функції як оберненої до показникової, виконуючи три кроки.

1. Функція у = а' зростаюча за а > 1, спадна - за 0 < а < 1, то­му вона є оборотною на всій області визначення. Враховуємо, що х є К, у є (0;+ ).

2. Розв'яжемо рівняння з двома невідомими у = а' стосовно невідомої х. Оскільки х - показник степеня, то, за означенням логарифма, х = 1оgау = у (у).

3. Поміняємо позначення незалежної і залежної змінних. Діс­танемо

у =log_ax , де х є (0; + ), у є К.

Означення. Функція, обернена до показникової функції у = a^х (а>0, а 1), називається логарифмічною і позначається у =log_ax

Побудувавши графік логариф­мічної функції як кривої, симетрич­ної графіку функції у = a^х стосовно прямої .у = х, учні «прочи­тають» спочатку властивості цієї функції за графіком, а потім дове­дуть їх аналітичне, послуговуючись теоремою про властивості взаємно обернених функцій.

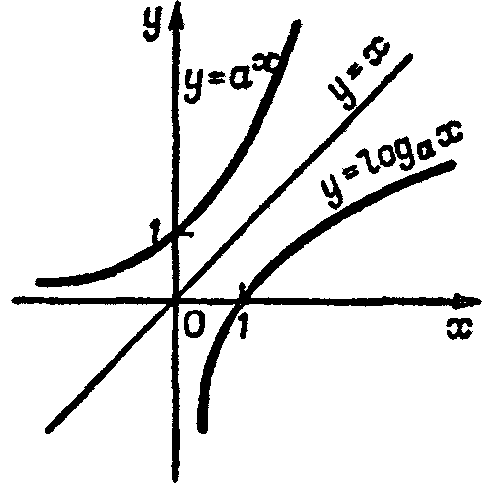
Степенева функція

З окремими випадками степеневої функції учні ознайомлювалися в 7 і 8 класах (у = х², у =х³ , у = ). Однак на тому етапі навчання термін «степенева функція» і відповідне означення ще не вводились, оскільки ще не відбулось розширення поняття степеня до степеня з дійсним показником.

Ввівши степінь з дійсним показником х^р, бачимо, що при за­даному дійсному значенні р кожному додатному х можна поставити у відповідність числове значення степеня х^р. Отже, при стало­му дійсному показнику р і змінному додатному х маємо функцію у = х^р, яку називають степеневою.

Властивості степеневої функції залежать від заданого значення р.

Доцільно розглянути різні можливі множини значень.

І. Нехай р — натуральне число.

Назвімо властивості функції.

1. Область визначення функції - множина всіх дійсних чисел. Область значень залежить від парності чи непарності р.

Якщо р — парне, то область значень у=х^р є множиною невід'ємних чи­сел, а якщо непарне, то – множиною R всіх дійсних чисел.

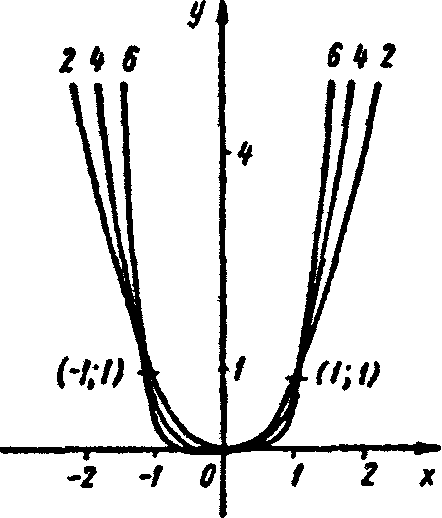
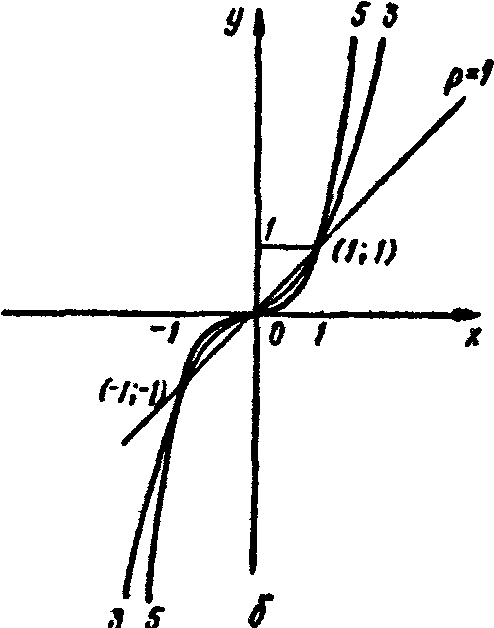
2. Функція парна при парному р і непарна - при непарному р.

3. При х = 0 і у = 0, при х = 1 і у = 1, тобто всі графіки степене­вих функцій проходять через початок координат і точку (1; 1).

4. При парному p функція зростає на проміжку [0; + ) і спадає на проміжку (- ; 0].

При непарному p функція зростає на всій області визначення.

5. При парному р графіки степеневих функцій схожі з графі­ком функції у = x² ,а при непарному - з графіком функції у=x³.

II. Нехай p - ціле від'ємне число.

У цьому випадку функція у = х^p визначена на множині всіх дійсних чисел, крім х=0. Коли p - парне від'ємне число, множиною значень функції є множина всіх додат­них чисел. Функція парна на області визначення і графік, скла­даючись з двох віток, симетричний щодо осі у; y=x^p зростає за x (- ; 0) і спадає за х (0; + ). Коли р - непарне від'єм­не число, множиною значень функції є об'єднання двох числових проміжків (- ; 0) і (0; + ). Функція непарна, спадна на всій області визначення, графік її симетричний стосов­но початку координат.

III. Нехай р - дробове додатне число, тобто р = , де т і п - натуральні числа.

З урахуванням означення степеня з дробовим показником сте­пенева функція матиме вигляд у=х = . 3 окремим випадком такої функції (у= ) учні ознайомились в курсі алгебри 8 класу.

При р = , р = степенева функція має вигляд у= , у= відповідно. Графіки двох останніх функцій схожі за формою з графіком функції y= . Неважко довести, що всі функції зроста­ючі, їхня область визначення залежить від показника кореня. Для парних п функція визначена лише для невід'ємних значень х, для непарних - за будь-якого дійсного х. У загальному випадку функ­ція у= розглядається лише при х 0.

Варто звернути увагу учнів на те, що функції у=х² і y= при х 0, у=х^з і у= при х R - взаємно обернені.