3 Корреляционно-регрессионный анализ

Создадим таблицу исходных данных (таблица 3.1). Построим корреляционную модель связи жилищного фонда по РБ (У) с включением трех факторов – численности постоянного населения (Х1), числа семей, нуждающихся в жилых помещениях (Х2) и ввода в действие водопроводных сетей (Х3).

Таблица 3.1 Исходные данные для корреляционно-регрессионного анализа
Годы	Жилищный фонд, тыс. м2	Численность постоянного населения, чел.	Число семей, состоящих на учете в качестве нуждающихся в жилых помещениях на конец года, единиц	Ввод в действие объектов коммунального хозяйства - водопроводные сети, км
	У	Х1	Х2	Х3
2000	71851,8	4119810	207375	77,09
2001	73471,9	4115176	202505	26,26
2002	74609,6	4108249	196272	90,52
2003	75930,3	4102274	192665	47,14
2004	77003	4094215	168126	119,79
2005	77834,5	4081349	131085	89,91
2006	79287,9	4066257	124663	112,47
2007	80864,8	4053439	63348	90,83
2008	83172	4054821	64697	55,19
2009	85783,8	4059373	73900	93,35
2010	87441,8	4068545	78345	48,66
2011	89380,1	4072085	74082	44,5
2012	91580,1	4064245	75593	111,2

Выполним корреляционно-регрессионного анализа с использованием ПП EXCEL. Для удобства анализа разобьем результаты статистической обработки на отдельные фрагменты.

Таблица 3.2 Корреляционная матрица
	У	Х1	Х2	Х3
У	1
Х1	-0,78233	1
Х2	-0,87594	0,96213	1
Х3	0,048591	-0,24024	-0,10205	1

Корреляционная матрица (таблица 3.2) содержит частные коэффициенты корреляции. Коэффициенты второго столбца матрицы характеризуют степень тесноты связи между результативным (У) и факторными признаками (Х1, Х2, Х3). Например, связь между жилищным фондом и численностью постоянного населения(r_УХ1 = -0,782) обратная, сильная; связь между жилищным фондом и числом семей, нуждающихся в жилых помещениях (r_УХ2 = -0,875) обратная, сильная; связь между жилищным фондом и вводом в действие водопроводных сетей (r_УХ3 = 0,048) прямая, слабая. Коэффициенты корреляции между факторами свидетельствуют об отсутствии мультиколлинеарности.

Таблица 3.3 Регрессионная статистика
Множественный R	0,907863
R-квадрат	0,824215
Нормированный R-квадрат	0,76562
Стандартная ошибка	3078,903
Наблюдения	13

Множественный коэффициент корреляции R = 0,907 показывает, что теснота связи между жилищным фондом и факторами, включенными в модель, сильная. Множественный коэффициент детерминации (R-квадрат) D = 0,8242, т.е. 82,42% вариации уровня жилищного фонда объясняется вариацией изучаемых факторов.

Таблица 3.4 Дисперсионный анализ
	df	SS	MS	F	Значимость F
Регрессия	3	400030050	133343350	14,06628	0,000958
Остаток	9	85316791,6	9479643,516
Итого	12	485346842

Проверим значимость коэффициента множественной корреляции, для этого воспользуемся F-критерием, для чего сравним фактическое значение F с табличным значением F_табл. При вероятности ошибки α = 0,05 и степенях свободы v1=k-1=3-1=2, v2=n-k=13-3=10, где k – число факторов в модели, n – число наблюдений, F_табл = 4,10. Так как F_факт = 14,06 > F_табл = 4,10, то коэффициент корреляции значим, следовательно, построенная модель в целом адекватна.

Таблица 3.5 Коэффициенты регрессии
	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	-1009106	655488,743	-1,539471673
Х1	0,272767	0,16217023	1,68198152
Х2	-0,1988	0,0634801	-3,131700829
Х3	22,00128	34,8585572	0,631158637

Продолжение таблица 3.5 Коэффициенты регрессии
P-Значение	Нижние 95%	Верхние 95%	Нижние 95,0%	Верхние 95,0%
0,158074	-2491925	473712,2	-2491925	473712,2
0,126867	-0,09409	0,639622	-0,09409	0,639622
0,012089	-0,3424	-0,0552	-0,3424	-0,0552
0,543631	-56,8543	100,8568	-56,8543	100,8568

Используя таблицу 3.5 составим уравнение регрессии:

У = - 1 009 106 +0,272Х₁ – 0,198 Х₂ + 22,001 Х₃.

Интерпретация полученных параметров следующая:

а0 = 11,9 – свободный член уравнения регрессии, содержательной интерпретации не подлежит;

а1 = 0,004 – коэффициент чистой регрессии при первом факторе свидетельствует о том, что при увеличении численности постоянного населения на 1 чел. жилищный фонд увеличится на 0,272 %, при условии, что другие факторы остаются постоянными;

а2 = -0,198 – коэффициент чистой регрессии при втором факторе свидетельствует о том, что при увеличении числа семей, нуждающихся в жилых помещениях на 1 ед. жилищный фонд сократится на 0,198 %, при условии, что другие факторы остаются постоянными;

а3 = 0,0049 – коэффициент чистой регрессии при третьем факторе свидетельствует о том, что при увеличении ввода в действие водопроводных сетей на 1 км жилищный фонд увеличится на 22%, при условии, что другие факторы остаются постоянными.

Проверку значимости коэффициентов регрессии осуществим с помощью t-критерия Стьюдента; для этого сравним фактические значения t-критерия с табличным значением t-критерия. При вероятности ошибки α = 0,05 и степени свободы v= n-k-1=13-3-1 =9, где k – число факторов в модели, n – число наблюдений, tтабл = 2,2622. Получим

t1факт = 1,681 < tтабл = 2,2622,

t2факт =-3,131 < tтабл = 2,2622,

t3факт = 0,631 < tтабл = 2,2622.

Значит, статистически значимыми не является ни один фактор.

Таблица 3.6 Описательная статистика
	У	Х1	Х2	Х3
Среднее	80631,6615	4081526	127127,385	77,4546154
Стандартная ошибка	1763,85875	6546,59513	16319,7395	8,34564416
Медиана	79287,9	4072085	124663	89,91
Мода	#Н/Д	#Н/Д	#Н/Д	#Н/Д
Стандартное отклонение	6359,68318	23604,0844	58841,6575	30,0906479
Дисперсия выборки	40445570,1	557152801	3462340658	905,447094
Эксцесс	-1,08389808	-1,39409	-1,87673783	-1,2385092
Асимметричность	0,38774939	0,45268578	0,27568893	-0,23469024
Интервал	19728,3	66371	144027	93,53
Минимум	71851,8	4053439	63348	26,26
Максимум	91580,1	4119810	207375	119,79
Сумма	1048211,6	53059838	1652656	1006,91
Счет	13	13	13	13
Уровень надежности(95,0%)	3843,11808	14263,8054	35557,6577	18,1835965

Средние значения признаков, включенных в модель У = 80 631,661 тыс. м2; Х1 = 4081 526 чел.; Х2 = 127 127,385 ед.; Х3 = 77,454 км.

Стандартные ошибки коэффициентов регрессии Sа0 = 1 763,858; Sа1 = 6 546,59; Sа2 = 16 319,739; Sа3 = 8,345.

Средние квадратические отклонения признаков σУ = 6 359,683 тыс. м2; σХ1 = 23 604,08 чел.; σХ2 = 58 841,65 ед. ; σХ3 = 30,09 км.

Зная средние значения и средние квадратические отклонения признаков, рассчитаем коэффициенты вариации для оценки однородности исходных данных

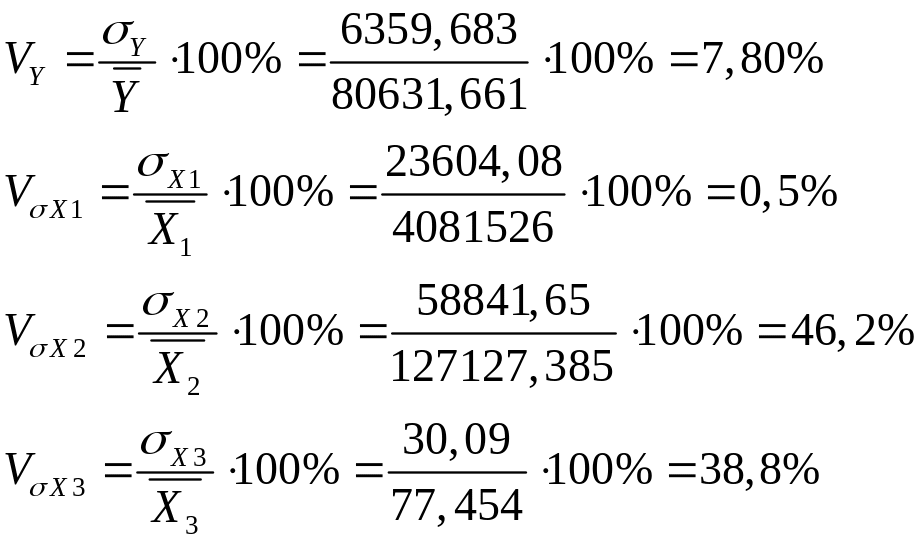
Вариация жилищного фонда и факторов, включенных в модель превышает допустимых значений (33-35%). В данном случае необходимо проверить исходную информацию и исключить те значения, которые значительно отличаются от средних значений.

Разные единицы измерения делают несопоставимыми коэффициенты регрессии, когда возникает вопрос о сравнительной силе воздействия на результативный признак каждого из факторов чистой регрессии. Выразим их в стандартизированной форме в виде бета-коэффициентов и коэффициентов эластичности.

Каждый из β-коэффициентов показывает, на сколько средних квадратических отклонений изменится уровень жилищного фонда , если соответствующий фактор изменится на свое среднее квадратическое отклонение.

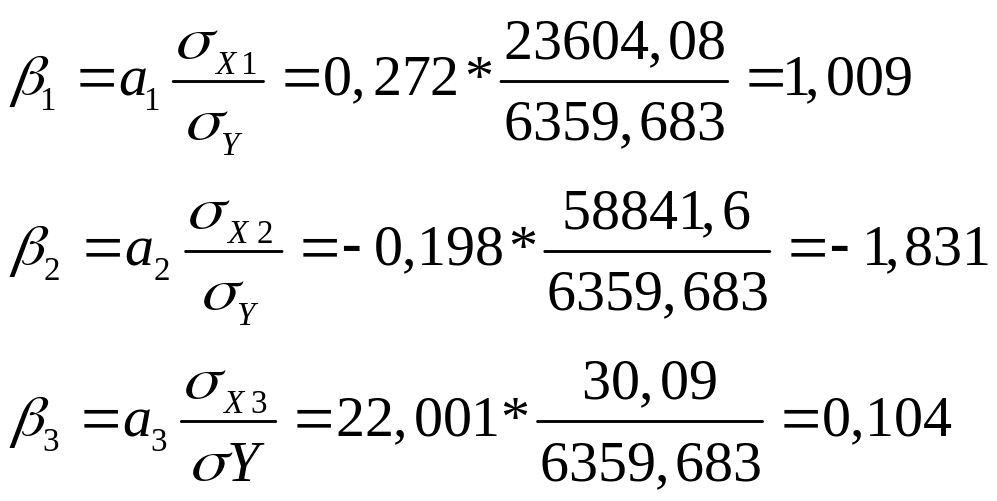
При увеличении численности постоянного населения и вводом в действие водопроводных сетей на 1 свое среднее квадратическое отклонение жилищный фонд увеличится соответственно на 1,009 и 0,104 от своего среднего квадратического отклонения. При увеличении числа семей, нуждающихся в жилых помещениях на 1 свое среднее квадратическое отклонение, жилищный фонд уменьшится на 1,831 от своего среднего квадратического отклонения.

Сопоставление β-коэффициентов показывает, что наиболее сильное влияние на варьирование жилищного фонда оказывают - численность постоянного населения, вторым – ввод в действие водопроводных сетей, третьим – число семей, нуждающихся в жилых помещениях.

Каждый из коэффициентов эластичности показывает, на сколько процентов изменится в среднем уровень жилищного фонда, если соответствующий фактор изменится на 1%.

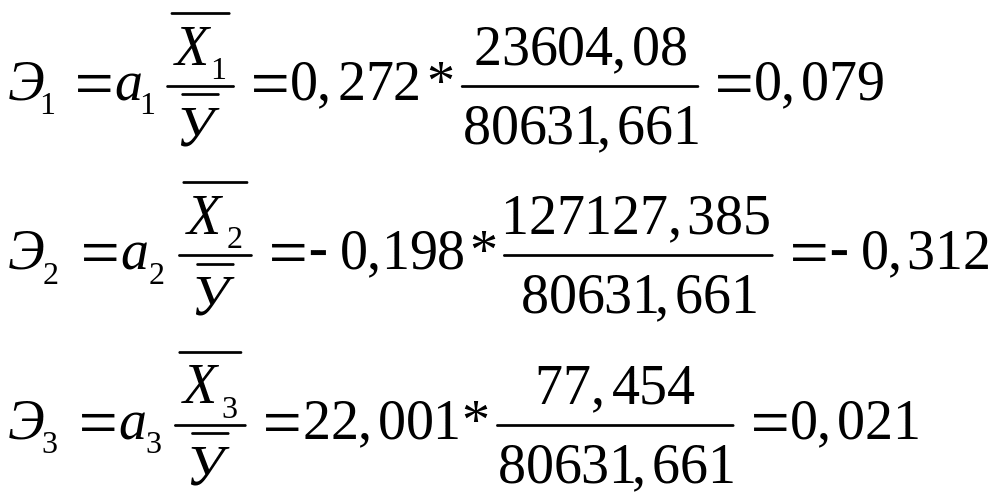
При увеличении численности постоянного населения и вводом в действие водопроводных сетей на 1% уровень жилищного фонда увеличится соответственно на 0,079% и 0,021%; при увеличении числа семей, нуждающихся в жилых помещениях на 1% уровень жилищного фонда снизится на 0,312%.

В таблице 3.7 приведены расчетные значения уровня жилищного фонда и отклонения фактических значений от расчетных. Расчетные значения получены путем подстановки значений факторов жилищного фонда в уравнение регрессии.

Если расчетное значение жилищного фонда превышает фактическое значение (остатки отрицательные), то имеются резервы увеличения жилищного фонда за счет факторов, включенных в модель, в противном случае (остатки положительные), имеются отсутствуют резервы увеличения жилищного фонда за счет факторов включенных в модель.

Таблица 3.7 Вывод остатка
Наблюдение	Предсказанное У	Остатки
1	75112,98	-3261,18
2	73698,81	-226,91
3	74462,28	147,32
4	72595,15	3335,15
5	76873,69	129,31
6	80070,64	-2236,14
7	77727,08	1560,82
8	85944,11	-5079,31
9	85268,76	-2096,76
10	85520,41	263,39
11	86155,32	1286,48
12	87876,88	1503,22
13	86905,48	4674,62

Так в 1, 2, 6, 8, 9 годы имелись резервы увеличения жилищного фонда .