2.4.6.2 Пример

Следующая иллюстрация показывает ключ к входным данным для типовой сети. Если для поиска выбраны следующие параметры:

• Число итераций поиска = 5,

• Сигма = 8^* квадратный корень (полное сопротивление R’),

тогда на единственной внешней итерации, все три мыслимых маршрута будут найдены.

Номер связи	Тип	Длина (м)	v0 (км/ч)	Пропускная способность (Pkw-E)	Imp*0 (мин)	Imp*0 (c)
1	20	5000	100	1200	03:00	180
2	20	5000	100	1200	03:00	180
3	20	5000	100	1200	03:00	180
5	20	5000	100	1200	03:00	180
6	20	5000	100	1200	03:00	180
7	20	5000	100	1200	03:00	180
8	30	16000	80	800	12:00	720
9	30	5000	80	800	03:45	225
10	40	10000	60	500	10:00	600
11	40	5000	60	500	05:00	300
Маршрут	Связи	Длина			Imp*0
1	1+8+9	26000			0:18:45	1125
2	1+2+3+5+6+7	30000			0:18:00	1080
3	10+11+5+6+7	30000			0:24:00	1440
Введите параметры: BPR функция пропускной способности при a = 1, b = 2, c = 1 Δbottom = 0.5, Δtop = 0.5 →Δ = 0.5 Назначение с Logit,  = 0.001

Иллюстрация 23: Импеданс в разгруженной сети, входные параметры для стохастического назначения

После завершения поиска определена независимость каждого маршрута. Она основана на подобии индивидуальных пар маршрутов, относительно времени t₀. Следующая иллюстрация показывает коэффициенты общности C. Они используются, чтобы вычислить независимость маршрутов:

Маршрут 1:

Маршрут 2:

Маршрут 3:

Пары маршрутов	t0ij	t0i	t0j	Cij
1,1	1125	1125	1125	1.00
1,2	180	1125	1080	0.16
1,3	0	1125	1440	0.00
2,1	180	1080	1125	0.16
2,2	1080	1080	1080	1.00
2,3	540	1080	1440	0.43
3,1	0	1440	1125	0.00
3,2	540	1440	1080	0.43
3,3	1440	1440	1440	1.00

Иллюстрация 24: Вычисление коэффициентов общности С для всех пар маршрутов

Доля для каждого маршрута вычислена от показателей его независимости и полного сопротивления Imp₀^* в разгруженной сети. Для Маршрута 1 доля вычислена, с использованием Logit-модели следующим образом:

Таким же образом, доли, показанные в таблицах, приводятся для Маршрутов 2 и 3. Интенсивность для каждого маршрута RVol₁ в первом итеративном шаге следует из произведения доли P и спроса F. Для Маршрута 1 вычисления следующие: 0.425 × 2000 = 849.4 PCU. Тогда полное сопротивление сети может быть вычислено, исходя из интенсивности маршрута и интенсивности связей (сравни c Иллюстрацией 42). Это приводит к полному сопротивлению Imp₁ маршрутов. Эти временные (промежуточные) результаты могут быть проверены в VISUM, если максимальное число внутренних итераций устанавливается к М = 1 в параметрах назначения.

маршрут	E	Imp*0	exp(Imp*0)×E	Доля P	RVol1	Imp1
1	0.8596	1125	0.279079049	0.425	849.4	2470
2	0.6264	1080	0.212737561	0.324	647.5	1961
3	0.6978	1440	0.165335421	0.252	503.2	2848
∑			0.657152032	1.000	2000

Иллюстрация 25: Интенсивность в первом шаге внутренней итерации m = 1

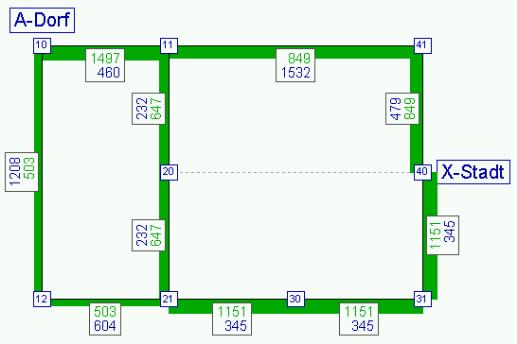
Иллюстрация 26: Интенсивность и времена прохождения связей после первого шага внутренней итерации m = 1

Для выбора маршрута во втором итеративном шаге вычисляется предполагаемый импеданс Imp₁^*. Начиная с Δ = 0.5, импеданс следует из формирования среднего значения Imp₀^* и Imp₁. На основе Imp₁^*, как в первом итеративном шаге, назначение сделано для 3 маршрутов. Для каждого маршрута временный (промежуточный) результат – RVol₂^′. Чтобы сгладить интенсивности между двумя итеративными шагами, используется метод MSA – Method of Successive Averages (метод Последовательных Средних Чисел)

Для m = 2, это приводит к следующей интенсивности для Маршрута 1:

Эта интенсивность маршрута тогда приводит к интенсивности связей и полному сопротивлению вторых итеративных шагов. Итерации повторяются, до тех пор, пока критерии завершения не станут удовлетворительными.

маршрут	E	Imp*1	exp(Imp)×E	Доля P	RVol2′	RVol2	Imp1
1	0.8596	1797.6	0.142432	0.3944	788.8	819.1	2405.2
2	0.6264	1520.7	0.136919	0.3791	758.3	702.9	2016.0
3	0.6978	2144.0	0.081775	0.2264	452.9	478.0	2785.6
∑			0.361126			2000

Иллюстрация 27: Интенсивности на втором шаге внутренней итерации m = 2