9.З. Резонансы в системе связанных контуров. Частные и сложные резонансы

Резонансом в системе связанных колебательных контуров на­зывается явление, при котором наступает максимум амплитуды любого из токов в контурах или напряжений на элементах кон­туров.

В системе связанных идеальных колебательных контуров (без потерь) амплитуда колебаний стремится к бесконечности. При этом максимум амплитуды наступает одновременно для всех ве­личин: токов в обоих контурах, напряжений на всех элементах. Условием резонанса в этом случае, как следует из выражений (9.8) и (9.9), является равенство нулю определителя Δ системы уравнений (9.5). Это равенство возможно при отсутствии потерь в схеме. При Δ = 0 амплитуды обоих токов I_т1 и I_т2 делаются бес­конечно большими.

При наличии потерь в контурах амплитуды токов в них имеют максимумы при разных значениях частоты. В таких случаях трудно говорить о резонансе во всей системе на какой-то частоте. Однако при малом затухании частоты максимумов практически совпадают. Поэтому при наличии затухания приближенно можно считать, что резонанс наступает во всей системе, когда наступает максимум амплитуды тока в любом из контуров. При решении практических задач иногда пользуются и другими приближенными определениями резонанса в системе, например: равенство нулю реактивной части комплексного сопротивления эквивалентного контура. Этому также приближенно соответствуют максимумы токов в обоих контурах.

Ограничимся рассмотрением высокодобротных контуров с ма­лым затуханием. Из соотношений (9.8), (9.9) и (9.18) следует, что в системе возникают резонансы при выполнении любого из условий:

или

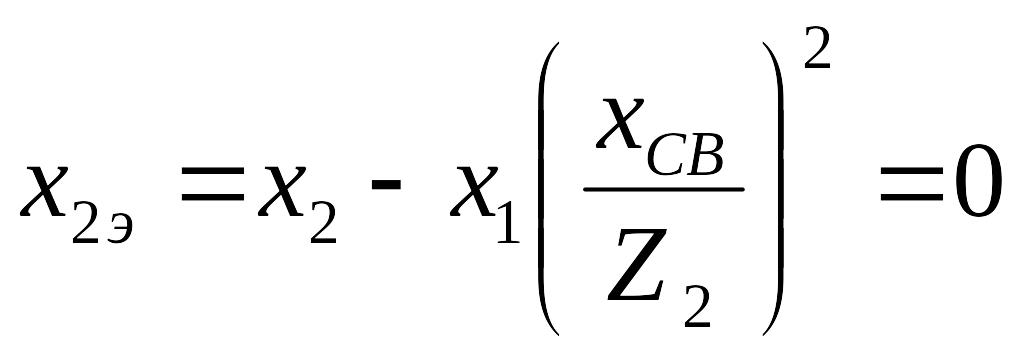. (9.25)

Кроме того, каждое из этих условий выполняется, если

, (9.26)

что также соответствует резонансу. При этих условиях токи в кон­турах, и в частности во втором контуре, принимают максимальные значения.

При настройке системы контуров в резонанс, если частота источника задана, эти условия могут быть выполнены разными путями: изменением реактивных параметров первого контура, второго контура или обоих контуров. Дополнительно, подбором сопротивления "связи между контурами, можно обеспечить наи­большее значение максимума амплитуды тока во втором контуре, достигаемого при резонансе, что следует непосредственно из вы­ражений (9.9), (9.12) и (9.18).

В соответствии с этим в системе различают: частные резонансы (первый, второй и основной, или индивидуальный) и слож­ные резонансы (первый, второй и полный).

Настройкой системы связанных контуров в резонанс при за­данной частоте сигнала называется подбор значений их парамет­ров, обеспечивающих выполнение условий резонанса, и в частно­сти достижение максимального значения тока во вторичном кон­туре. При настройке на частный резонанс выполнение условий резонанса достигается подбором значений параметров раздельно того или иного контура либо обоих контуров. Настройка на слож­ный резонанс осуществляется после настройки на один из частных резонансов путем подбора связи между контурами. При этом до­полнительно к условиям резонанса выполняются и условия пере­дачи максимально возможной мощности из первого контура во второй.

Первый частный резонанс в системе связанных контуров до­стигается изменением реактивных параметров первого контура. Параметры второго контура и глубина связи при этом остаются неизменными:

.

Резонанс достигается при выполнении условия (9.24), когда

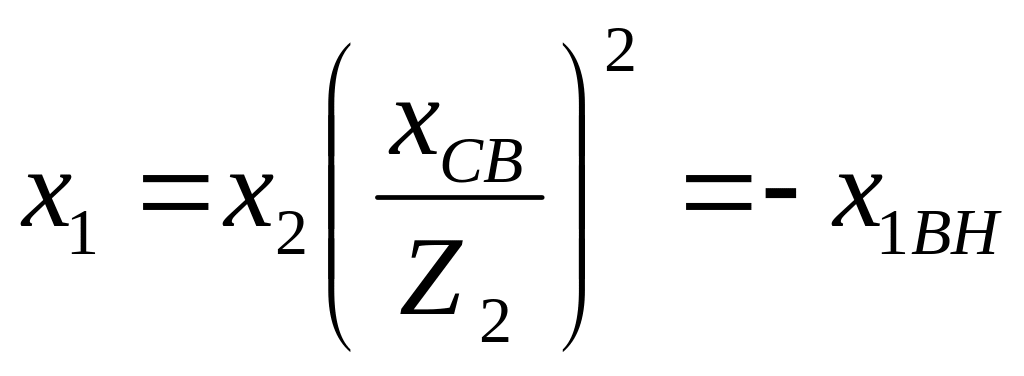(9.27)

что и является условием первого частного резонанса.

Максимум вторичного тока находим из соотношения (9.13) с учетом выражений (9.8), (9.11) и (9.24):

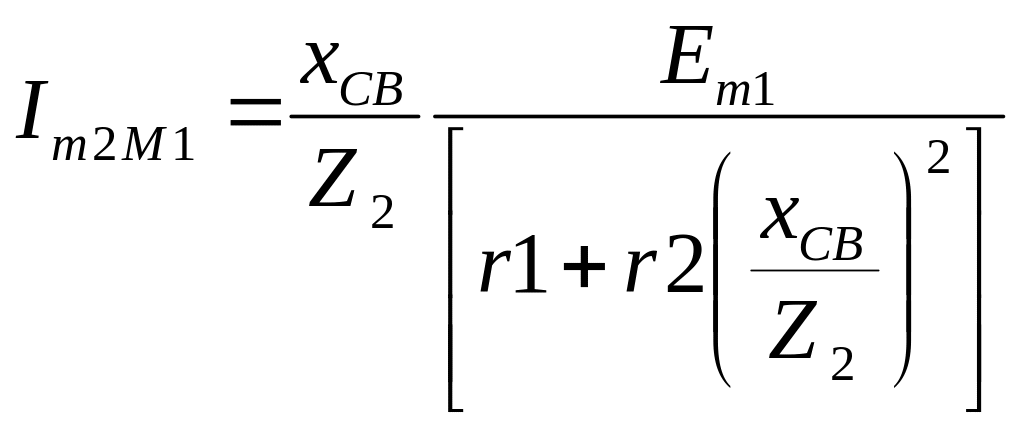(9.28)

Примером использования первого частного резонанса служит настройка выходного колебательного контура генератора сигналов высокой частоты (ГСВЧ), индуктивно связанного с емкостной на­грузкой, например с антенной (рис. 9.5).

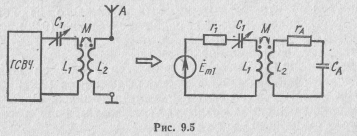
Второй частный резонанс достигается изменением реактивных параметров второго контура. Параметры первого контура и глу­бина связи остаются неизменными:

.

Резонанс достигается при выполнении условия (9.25), когда

, (9.29)

что и является условием второго частного резонанса.

Максимум вторичного тока в этом случае находим из выраже­ния (9.9) с учетом формул (9.12), (9.18) и (9.25):

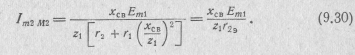
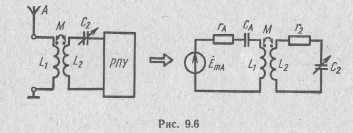
Примером использования второго частного резонанса служит настройка входного колебательного контура радиоприемного уст­ройства (РПУ), индуктивно связанного с антенной (рис. 9.6). Первым контуром здесь является антенна, а вторым — перестраи­ваемый входной контур приемника.

Основной или индивидуальный резонанс достигается, если оба контура, будучи взяты раздельно, при отсутствии связи между ними индивидуально настроены в резонанс:

.

При этом реактивные сопротивления каждого из контуров в отдельности равны нулю и выполняется условие (9.26) или

. (9.31)

т. е. при основном резонансе оказываются также одновременно выполненными и условия обоих частных резонансов (9.27) и (9.29). Равенство (9.31) есть условие основного резонанса. Практически индивидуальная настройка контуров производится при очень сла­бой связи между ними.

Значение амплитуды вторичного тока при основном резонансе получаем из выражения (9.28) или (9.30), учитывая формулу (9.31):

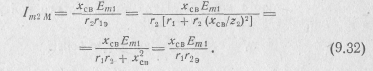
Сравнивая амплитуды вторичного тока в формулах (9.28), (9.30) и (9.32) при частных резонансах, отметим, что при основ­ном резонансе амплитуда значительно превосходит значения, до­стигаемые при частных резонансах. Поэтому обычно стремятся настроить на частоту сигнала каждый из контуров индивидуально, если конструкция всей системы это позволяет.

Пример 9.2.

Известны параметры двух индуктивно связанных колебательных контуров (см. рис. 9.1,a): r₁= 15 Ом; r₂=100 Ом; L_l = 250 мкг; L₂=300 мкг; С₂=1150 пФ. При такой емкости С₁ будет выполнено условие первого частного резонанса, если частота сигнала f=O,6 мгц, а коэффициент связи K=16,5%?

Решение.

1. Из условия первого частного резонанса (9.27)

Поэтому

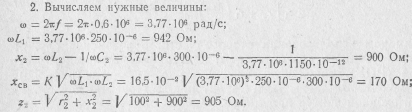
3. Вычисляем требуемое значение емкости C_l:

Анализируя выражения для амплитуды вторичного тока при частных резонансах в формулах (9.28), (9.30) и (9.32), лёгко cеделать вывод, что при соответствующем подборе сопротивления связи можно увеличить достигаемый максимум тока I_т2.

Режим системы, при котором выполнено условие одного из частных резонансов и подобрана наивыгоднейшая связь между контурами, называется сложным резонансом.

Первый сложный резонанс достигается после настройки си­стемы на первый частный резонанс путем подбора оптимальной связи. Обращаясь к выражению (9.28) и исследуя функцию на экстремум, находим условие первого сложного резонанса:

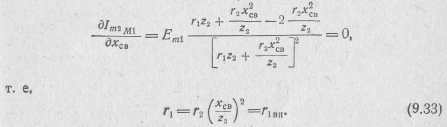
Этому условию соответствует оптимальная связь с

. (9.34)

Подставляя ее значение в формулу (9.28), получаем значение вторичного тока, достигаемое при подборе наивыгоднейшей связи:

(9.35)

Здесь

- (9.35)

модуль передаточной проводимости системы, настроенной на сложный резонанс.

Такое же значение вторичного тока будет получено, если пер­воначально предположить, что система контуров настроена на вто­рой частный резонанс. Разница будет лишь в требуемой оптималь­ной связи.

Второй сложный резонанс достигается после настройки си­стемы на второй частный резонанс подбором оптимальной связи.

Обращаясь к выражению (9.30) и исследуя на экстремум функ­цию , находим условие второго сложного резонанса:

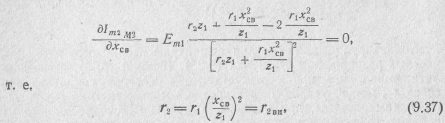
чему соответствует оптимальная связь с

(9.38)

Подстановка выражения (9.38) в формулу (9.30) приводит к равенству (9.35).

При настройке на первый или второй сложный резонанс изме­нение х_св нарушает условие соответствующего частного резонанса (9.27) или (9.29). Поэтому после изменения х_св контуры подстраи­вают для восстановлення этого условия, после чего связь изме­няется и т. д. Таким образом, методом последовательных прибли­жений достигается максимально возможное значение вторичного тока, хотя это и усложняет настройку.

Полный резонанс в системе связанных контуров достигается после ее настройки на основной резонанс путем дальнейшего под­бора оптимальной связи. При этом наибольшее значение вторич-· ного тока будет достигнуто, когда

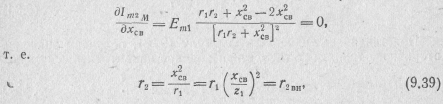
что соответствует условию полного резонанса и оптимальной связи:

. (9.40)

Подставляя это значение сопротивления связи в формул) (9.32), также придем к выражению (9.35). Таким образом, при всех сложных резонансах достигается одно и то же максимально возможное значение вторичного тока .

Полным резонансом называется разновидность сложного резо­нанса, при котором каждый из контуров настроен индивидуально Настройка на полный резонанс проста. Она не требует последова тельных приближений, так как условие основного резонанса (9.31) не зависит от величины х_св.

Сравнение формул сопротивлений связи (9.34), (9.38) и (9.40), при которых достигается тот или иной сложный резонанс, показы­вает, что для получения наибольшего значения вторичного тока I_m2MM при полном резонансе требуется наименьшая связь:

так как

так как

Сложные резонансы достигаются при одновременном выполне­нии двух условий: частного резонанса (9.27), (9.29) или (9.31) и оптимальной связи (9.34), (9.38) или (9.40). Учитывая это, усло­вия сложного резонанса можно выразить в более общей форме:

или . (9.41)

Эти условия одновременно являются и условиями передачи максимума активной мощности из первого контура во второй.

Активное сопротивление второго контура r₂ обычно представ­ляет сумму собственного сопротивления контура r_K2 и сопротив­ления нагрузки r_H, причем r_K2<<r_H. Поэтому а мощность, выделяемая во втором контуре, представляет активную мощность в нагрузке . При сложных резонансах в нагрузке выделяется наибольшая активная мощность

(9.42)

Этому соответствует КПД, равный 50%. Мощность, отдаваемая источником сигнала в таком режиме, потребляется поровну в ак­тивных сопротивлениях первого и второго контуров.

Наименьшее возможное значение сопротивления связи (9.40), при котором обеспечивается максимум вторичного тока, назы­вается оптимальным. Степень отклонения связи от оптимальной оценивается с помощью фактора связи:

. (9.43)

Фактор связи можно выразить через коэффициент связи, учи­тывая выражения (9.4) и (9.40):

Связь называется оптимальной, если А =1. Ей соответствует оптимальный коэффициент связи

· (9.45)

При идентичных контурах ( )

. (9.46)

Оптимальный коэффициент связи тем меньше, чем больше доб­ротность контуров. Для радиотехнических контуров Q=100÷500 и коэффициенты связи обычно исчисляются единицами или долями процента,

Пример 9,3.

Антенный контур L_l, С_а, r_a индуктивно связан с входным контуром радио­приемника l₂, С₂, r₂ (см. рис. 9.6). Оба контура настроены на частоту сигнала f₀=2,5 МГц. В антенном контуре наводится э. д. с. Е_{m а}=100 мкВ. Параметры контуров: r₁=10 Ом; L_l = 200 мкг; r₂=20 Ом; L₂=400 мкг. Определить напря­жение на емкости С₂ при настройке системы на полный резонанс и коэффициент связи, который для этого требуется.

Решение.

1. Требуемый коэффициент связи: