9.2. Эквивалентные схемы и комплексные функции системы двух связанных контуров

Для анализа процессов в системе из двух связанных контуров обратимся к методу вносимых сопротивлений, являющемуся раз­новидностью метода преобразований цепи. Суть этого метода за­ключается в эквивалентной замене системы связанных контуров одноконтурной схемой, анализ которой не представляет трудности. Такую замену делают следующим образом:

одним из известных методов определяют токи в обоих кон­турах;

полученным выражениям приводят в соответствие две эквива­лентные схемы (на базе тока в первом и на базе тока во втором контуре).

Название методу дают компоненты комплексных сопротивле­ний получаемых эквивалентных схем.

Для составления системы уравнений, описывающих систему связанных контуров, обратимся к Т-образной обобщенной схеме

(рис. 9.3, а), для которой справедливы контурные урав­нения¹:

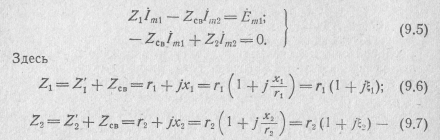
сумма сопротивлений элементов первого и второго контуров соот­ветственно.

Решение этой системы уравнений дает токи в связанных кон­турах:

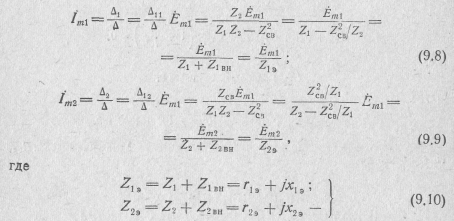
эквивалентные сопротивления первого и второго контуров;

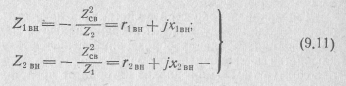
¹ Для схемы, например, с индуктивной связью (см. рис. 9.1, а):

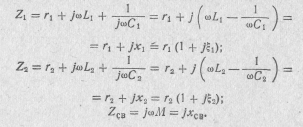
вносимые сопротивления;

-- (9.12)

э. д. с., наводимая во втором контуре.

Ток во втором контуре можно выразить через ток в первом контуре с помощью выражений (9.8) и (9.9):

(9.13)

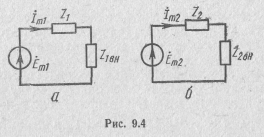
Выражениям (9.8) и (9.9) соответствуют одноконтурные схемы (рис. 9.4). Схема (рис. 9.4,а), в которой ток определяется выра­жением (9.8) и равен току в первом контуре, называется эквива­лентной схемой системы связанных контуров на базе тока в пер­вом контуре. Схема (рис. 9.4,6), в которой ток в соответствии с формулой (9.9) равен току во втором контуре, называется экви­валентной схемой на базе тока во- втором контуре. С помощью этих схем токи в контурах определяются непосредственно по за­кону Ома.

Рассмотрим параметры эквивалентных схем для наиболее часто встречающегося на практике случая, когда r_СВ= 0, т. е.

(9.14)

Из формулы (9.11) с учетом выражений (9.6) и (9.7) получаем:

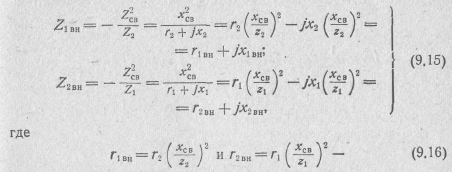
активные составляющие вносимых сопротивлени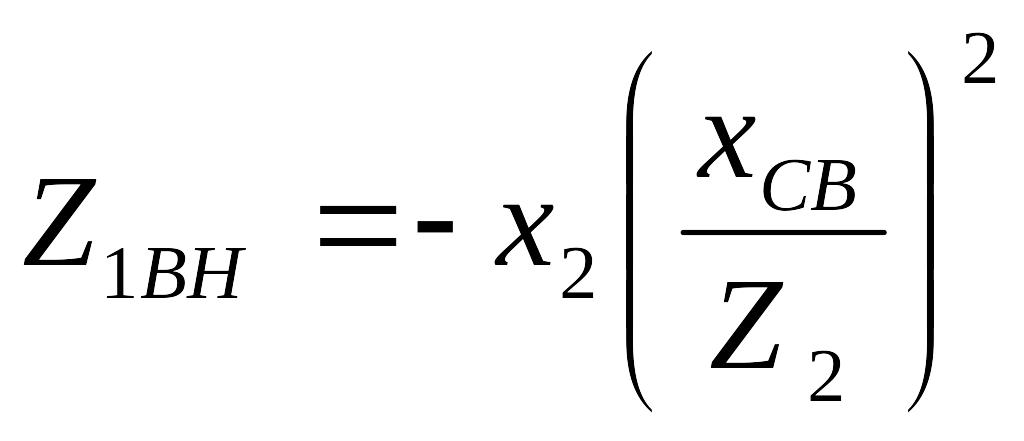й;

и 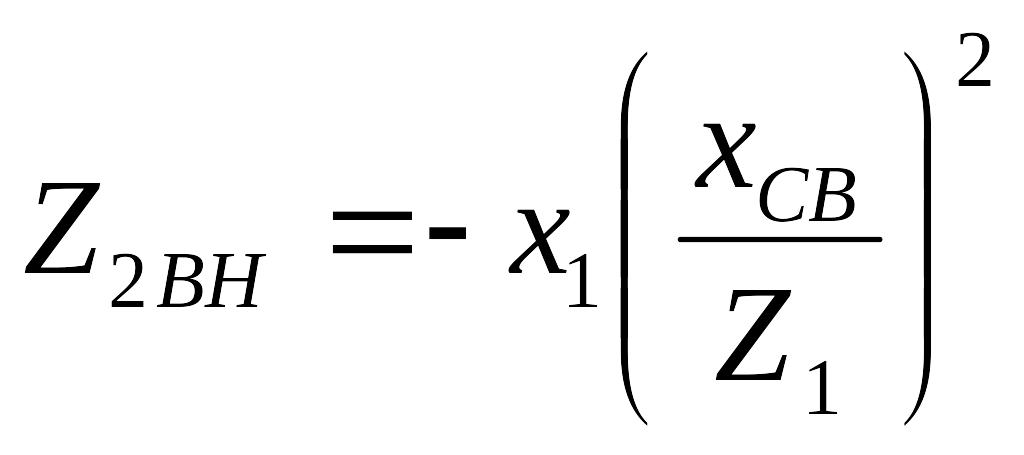(9.17)

реактивные составляющие вносимых сопротивлений.

Вносимые сопротивления учитывают взаимное влияние связан­ных контуров друг на друга. Сопротивления и учитывают влияние соответственно второго контура на первый и первого — на второй. Сопротивление r_lBH в первой эквивалентной схеме (см. рис. 9.4,а) учитывает потери во втором контуре. Сопротив­ление r_2BH во второй эквивалентной схеме (рис. 9.4, б) учитывает потери в первом контуре.

Реактивные сопротивления x_lBH и x_2BH представляют реактив­ность, вносимую в один из контуров за счет другого, и таким об­разом учитывают влияние расстройки одного из контуров на другой, Значения этих сопротивлений всегда обратны по знаку реактивности контура, влияние которого они учитывают. Напри­мер, сопротивление x_lBH всегда обратно по знаку реактивности второго контура x₂. Это значит, что при индуктивной расстройке второго контура ( и ) в первый контур вносится емкостная расстройка, так как при этом 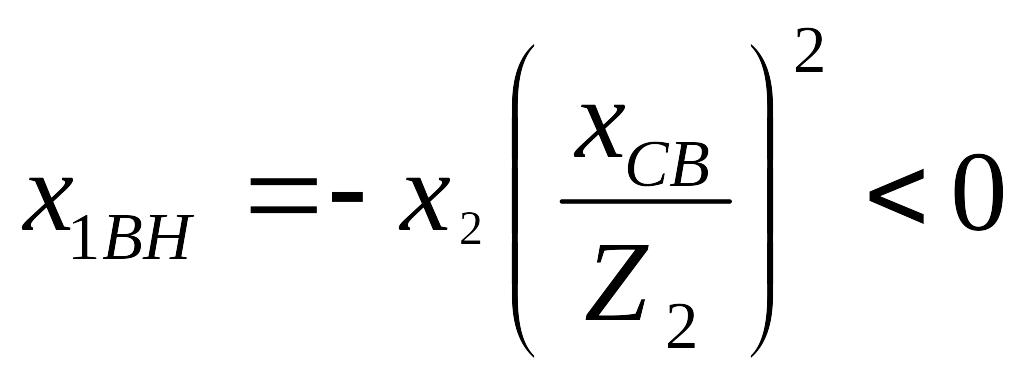и , и наоборот.

Таким образом, для эквивалентных сопротивлений каждого из контуров на основании выражений (9.8) — (9.17) можно записать:

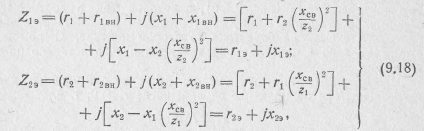
Выражения (9.8), (9.9) для токов в контурах можно представить и иначе, выразив токи через комплексные входные и передаточные функции системы:

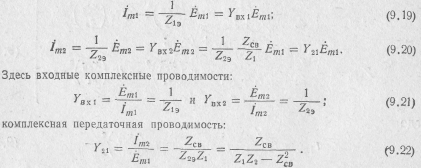
Соотношения (9.5) — (9.22) получены для Т-образной обобщен­ной схемы. Для дуальной ей П-схемы легко получить дуальные выражения и прийти к выводам, аналогичным для случая Т-схем.

В качестве примера найдем передаточное сопротивление для П-образной обобщенной схемы (см. рис. 9.3,6), используя ее матрицу узловых проводи-мостей:

Как следует из выражения (6.24),