8.5. Особенности применения параллельных колебательных контуров

Основным назначением параллельных колебательных контуров является обеспечение частотной избирательности. В радиотехниче­ских устройствах они применяются для выделения колебаний, за­нимающих определенную частоту или полосу частот. Примерами могут служить различные избирательные усилители на электрон­ных лампах и транзисторах, входные каскады радиоприемников, смесителей частоты, автогенераторы гармонических колебаний и др.

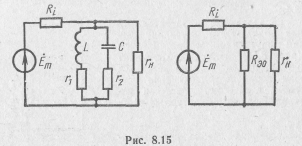
Чаще параллельный колебательный контур включается парал­лельно нагрузке и источнику (рис. 8.15). При этом выходное на­пряжение снимается с контура, а его частотно-избирательные свойства описываются резонансными характеристиками по напря­жению. Нагрузка и внутреннее сопротивление источника в такой схеме шунтируют колебательный контур, снижая его эквивалент­ную добротность и расширяя полосу пропускания. Учет влияния сопротивления нагрузки r_н на контур аналогичен учету сопротив­ления R_ш в схеме (см. рис. 8.11). Чтобы снизить шунтирующее Действие нагрузки и источника в такой схеме, необходимо, чтобы

значения их сопротивлений были достаточно высокими. Этому удовлетворяют, например, схемы на электронных лампах. Однако в транзисторных схемах, характеризующихся, как правило, низ-

к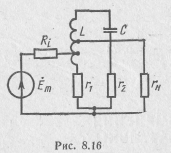 ими внутренними сопротивлениями, эффективное использование простого параллельного контура из-за сильного шунтирования практически невозможно. В этих случаях используются сложные

параллельные контуры (рис. 8.16). Соответствующий выбор коэффициентов включения позволяет значительно сни­зить эквивалентное сопротивление сложного параллельного колебательно­го контура относительно точек подклю­чения и избежать его шунтирования. Параллельный контур используется и в схеме с последовательным вклю­чением нагрузки и источника сигнала (рис. 8.17). При этом выходной сигнал пропорционален току, потребляемому контуром, а частотно-избирательные свойства схемы описываются резонансными характеристиками по току. Использование парал­лельного колебательного контура между источником и нагрузкой

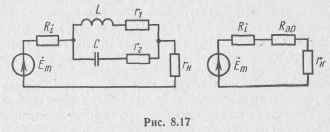
эффективно, если внутреннее сопротивление источника и включен­ной последовательно с ним нагрузки мало. Эквивалентная доб­ротность контура в таких схемах невелика.

Основой для определения полосы пропускания в схеме с последовательным включением контура являются резонансные кри-

вые по току (рис. 8.18). Полоса пропускания параллельного кон­тура по току рассчитывается как интервал частот вблизи резо­нанса, на границах которого ток, потребляемый контуром, увели­чивается в раза от своего минимального значения при резонансе.

П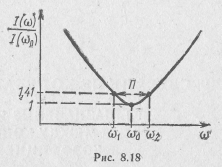 римером последователь­ного включения параллельного колебательного контура явля­ется фильтр-пробка на входе радиоприемника (рис. 8.19,а). Контур в этой схеме задержи­вает сигналы с частотами в пределах полосы пропускания по току, так как в этом интер­вале частот его эквивалентное сопротивление наибольшее. Для подавления нескольких сигналов на разных частотах последо­вательно включаются соответственно несколько параллельных кон­туров (рис. 8.19, б), настроенных на подавляемые частоты,

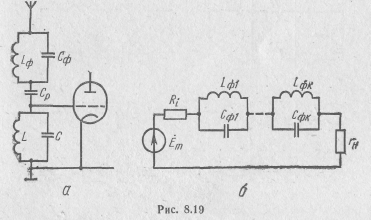
Если при параллельном включении параллельный контур слу­жит для выделения сигналов, то при последовательном включе­нии, наоборот, для их подавления. Параллельный колебательный контур, как и последовательный, широко используется также в электрических фильтрах различного назначения.

9. СВЯЗАННЫЕ КОЛЕБАТЕЛЬНЫЕ КОНТУРЫ

9.1. НАЗНАЧЕНИЕ И ВИДЫ СВЯЗИ

МЕЖДУ КОНТУРАМИ.

КОЭФФИЦИЕНТ СВЯЗИ

Частотно-избирательные свойства одиночных колебательных контуров невысоки (Kп=0,1). Более высокая избирательность

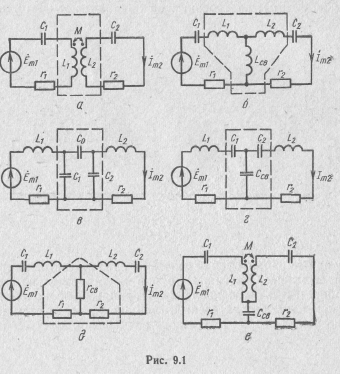
достигается в системе связанных колебательных контуров. Про­стейшей является система из двух связанных контуров (рис. 9.1 и 9.2), анализом которой и ограничимся ниже. Колебательные

контуры являются связанными, если процессы, протекающие в них, влияют один на другой.

Контур, к которому подключают источник сигнала, называется первичным, а контур, с которого снимается выходной сигнал,— вторичным. По отношению к колебательному контуру источник

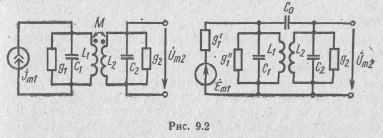
может быть включен последовательно или параллельно. В зави­симости от этого различают схемы последовательного (см. рис. 9.1) и параллельного (см. рис. 9.2) питания. В первом слу­чае источник сигнала удобно представлять источником э.д.с., а во втором — источником тока.

Наиболее распространенным видом связи является индуктив­ная связь, осуществляемая путем взаимоиндукции (рис. 9.1,а). К числу других видов связи относятся кондуктивная (рис. 9.1,6), емкостная (рис. 9.1,в, г), резистивная (рис. 9.1,д), комбинирован­ная (рис. 9.1, в).

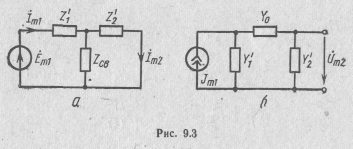
Любую систему связанных контуров можно представить Т- или П-образной эквивалентной обобщенной схемой (рис. 9.3). Эти схемы дуальны и могут быть взаимно преобразованы одна в дру­гую. В Т-схеме (рис. 9.3,а) сопротивления и представ­ляют комплексные сопротивления первого и второго контура без учета сопротивления Z_CB ветви, общей для обоих контуров. В П-схеме (рис. 9.3, б) проводимости и представляют комплексные проводимости первого и второго контура без учета проводимости Y₀ ветви, связывающей оба контура.

Связь между контурами характеризуют сопротивлением связи Z_CB. Сопротивлением связи называется сопротивление, общее для обоих контуров. Эта величина легко находится из Т-образной эквивалентной схемы. Для расчета сопротивления связи в П-схемах их нужно предварительно преобразовать в, эквивалентную T-схему. Однако при достаточно слабой связи для таких схем можно считать .

Более удобным и универсальным параметром количественной оценки любого вида связи между контурами является коэффициент связи. Для его определения выделяют участок схемы, образован­ный элементом связи и элементами связанных контуров, одно­именными с элементом связи, например, как показано пунктиром на рис. 9.1. Такой участок имеет четыре внешних зажима и назы­вается четырехполюсником связи. Коэффициентом связи назы­вается среднее геометрическое значение модулей передаточных функций по напряжению четырехполюсника связи в прямом и об­ратном направлениях:

. (9.1)

Для индуктивной связи с помощью схем рис. 9.1, а, 9.3, а по­лучаем:

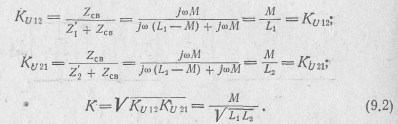
В общем случае при реактивном сопротивлении связи для ко­эффициента связи можно записать

(9.3)

где х₁ и х₂ — реактивные сопротивления элементов первого и вто­рого контуров, одноименных с элементами связи.

Коэффициент связи не может быть больше единицы. Его зна­чения находятся в пределах . Так как в радиотехнике наибольший интерес представляют режимы контура вблизи резо­нанса, когда индуктивное и емкостное сопротивления его элемен­тов , выражение (9.3) можно переписать:

. (9.4)

Па практике пользуются следующей условной оценкой связи между контурами: очень слабая связь ( ), слабая связь ( ), сильная связь ( ), очень сильная связь ( ).

Системы связанных колебательных контуров чаще работают при слабой связи. Связь между контурами обычно осуществляют через реактивность. Резистивная связь используется, когда тре­буется, чтобы сопротивление связи не зависело от частоты.

Пример 9.1.

Определить емкость конденсатора связи в схеме с внутренней емкостной связью (пи. рис. 9.1,г), если С₁ = С₂=100 пФ, а коэффициент связи равен 0,1. Решение. Из формулы (9.3) следует:

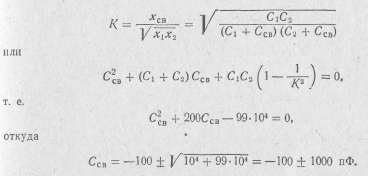
Так как физический смысл имеют лишь положительные значения емкости С_св, то С_св =900 пФ.