8.3. Полоса пропускания и коэффициент прямоугольности

Г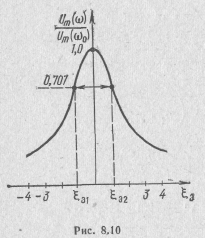 лавным назначением параллельного резонансного контура является выделение на контуре колебаний напряжения в опреде­ленной полосе частот. Поэтому основой для определения его по­лосы пропускания является резо­нансная кривая по напряжению. Полосой пропускания параллель­ного колебательного контура назы­вается интервал частот вблизи ре­зонанса, на границах которого ам­плитуда напряжения на контуре снижается до уровня = 0,707 своего максимального значения (рис. 8.10).

Для нахождения граничных ча­стот подставим в уравнение (8.19) значение этого уровня:

(8.20)

Отсюда следует, что границам полосы пропускания соответ­ствует эквивалентная обобщенная расстройка . Далее ана­логично выражениям (7.42) — (7.47) получаем сходные выражения:

(8.21)

. (8.22)

Полоса пропускания параллельного контура определяется его эквивалентной добротностью Q_э и, следовательно, зависит не только от собственной добротности контура Q, но и от внутреннего сопро­тивления r_i источника. Чтобы расширить полосу пропускания, не­обходимо уменьшить эквивалентную добротность контура. Как следует, например, из формулы (8.15), это возможно двумя пу-

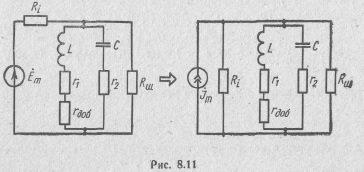
тями (рис. 8.11): увеличением активного сопротивления г включением в ветви контура добавочного сопротивления r_ДОБ и дополнительным шунтированием контура сопротивлением R_ш = 1/g_ш·

Включение в ветви контура добавочного сопротивления приводит к снижению его добротности:

Дополнительное шунтирование контура уменьшает общее ее противление, шунтирующее контур:

В итоге исходя из выражения (8.15) находим

где

Отсюда выражение для полосы пропускания

(8.24)

В нем дополнительные слагаемые учитывают влияние сопро­тивлений и на ширину полосы пропускания.

Коэффициент прямоугольности параллельного колебательного контура численно равен коэффициенту прямоугольности последо­вательного контура:

(8.25)

Это свидетельствует о том, что их избирательные свойства оди­наковы.

Пример 8.3.

Рассчитать полосу пропускания параллельного контура в схеме (см. рис. 8.8, пример 8.2) и определить значение шунтирующего сопротивления R_ш, необходимого для расширения этой полосы в 1,5 раза.

Решение.

1. Полоса пропускания контура в схеме:

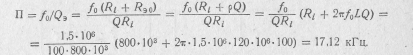
2. В соответствии с (8.24) включение R_ш увеличивает относительную полосу пропускания на величину ρ/ R_ш, что по условию задачи составляет 0,5П₀. Отсюда

т. е. для расширения полосы пропускания в k=1,5 раза необходимо выбрать

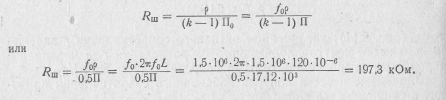
8.4. Сложные параллельные колебательные контуры

Если хотя бы в одной из ветвей простого параллельного коле­бательного контура (см. рис. 8.1) включить две разнородные ре­активности (рис. 8.12), то полученные схемы приобретают важные

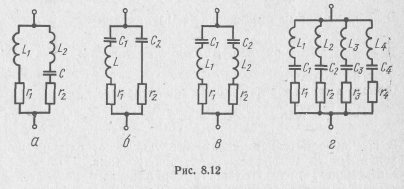
для их практического применения свойства. Такие схемы назы­ваются сложными параллельными колебательными контурами II вида (рис. 8.12,а), III вида (рис. 8.12,б) и IV вида (рис.8.1.2, в)•

Они позволяют согласовать эквивалентное сопротивление контура с сопротивлением нагрузки, уменьшить эффект шунтирования кон­тура, а также обладают свойством подавления дополнительных ча­стот. Обратимся к наиболее общей схеме (рис. 8.12, в) для ана­лиза особенностей таких контуров.

Подставляя в условие резонанса токов (8.1) значения реактив­ных сопротивлений ветвей контура и пренебрегая в случае высоко-добротных контуров сопротивлениями r₁ и r₂, получим

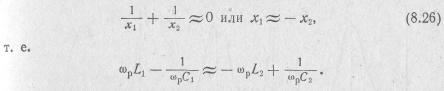
Отсюда следует, что резонансная частота сложного параллель­ного колебательного контура определяется его эквивалентной ин­дуктивностью l = l₁ + l₂ = l_э и эквивалентной емкостью

(8.27)

Аналогично определяются и его волновое сопротивление, доб­ротность, затухание:

где r = r₁ + r₂.

Эквивалентную индуктивность, емкость, активное сопротивление сложного параллельного контура можно определить путем после­довательного обхода его ветвей.

Так как при резонансе реактивная проводимость контура b = b₁ + b₂ равна нулю, то его эквивалентное сопротивление при резонансе имеет активный характер и определяется суммой актив­ных проводимостей ветвей:

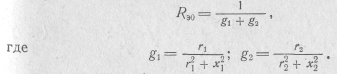
Отсюда, учитывая выражение (8.26) и пренебрегая и из-за малости, находим

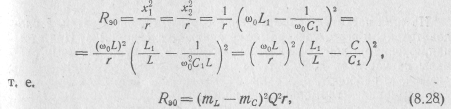
где -коэффициент включения индуктивности;

-коэффициент включения емкости.

Эквивалентное сопротивление сложного параллельного колеба­тельного контура при резонансе зависит от коэффициентов вклю­чения и и может быть значительно меньшим, чем у про­стого параллельного контура.

Коэффициенты включения и могут быть в пределах . Это позволяет в широких пределах менять эквивалент­ное сопротивление сложного контура, не изменяя его вторичные параметры Q, ρ, ω₀, что имеет важное практическое значение.

В схемах контуров II и III вида коэффициенты и соответственно равны нулю.

Анализируя схемы сложных параллельных колебательных кон­туров, можно выявить в них возможность дополнительных резонансов, которые возникают в параллельных ветвях контура, содер­жащих последовательное соединение разнородных реактивностей L и С. Частоты дополнительных резонансов определяются пара­метрами этих ветвей:

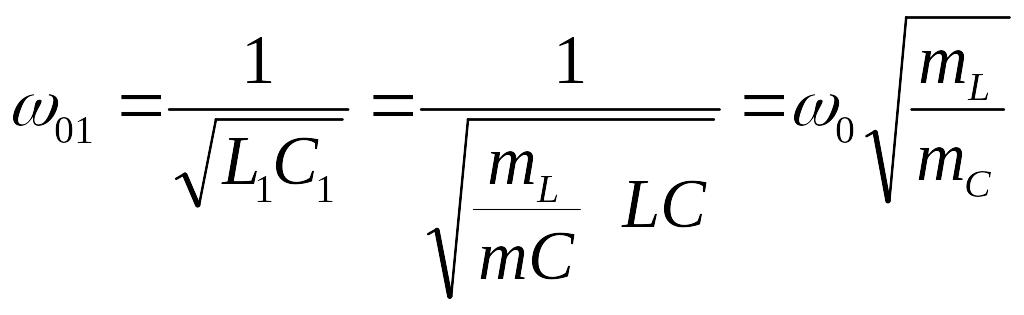(8.29)

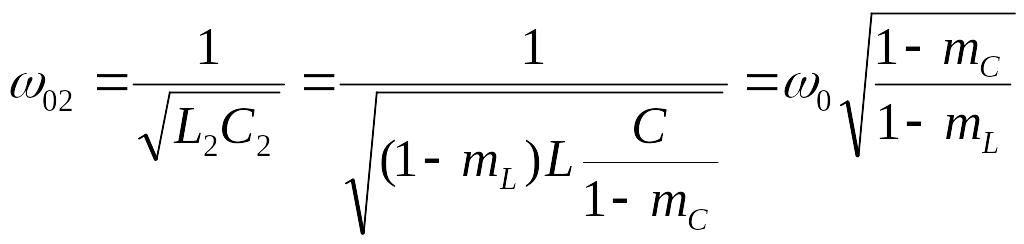(8.30)

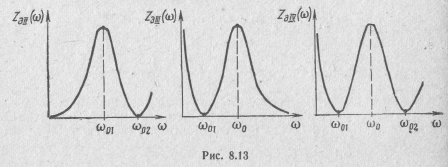
На этих частотах сопротивление соответствующей ветви, а, сле­довательно, и всего контура резко снижается (рис. 8.13). При этом напряжение на контуре падает практически до нуля. Поэтому сиг­налы на частотах дополнительных резонансов контуром не выде­ляются, а, наоборот, подавляются. Это используется для фильтра­ции гармоник — гармонических колебаний с кратными частотами.

Для подавления ряда гармоник применяются многозвенные кон­туры, содержащие несколько параллельных ветвей, настроенных на частоты, которые необходимо подавить (см. рис. 8.12,г).

Пример 8.4.

С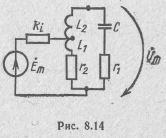 ложный параллельный колебательный контур II вида подключен к источнику сиг­нала с низким внутренним сопротивлением R_i = 2 кОм (рис. 8.14). Найти коэффициент включения, при котором на частоте резонанса в контур будет передана максимально воз­можная мощность, т. е. будет обеспечен ре­жим согласования. Параметры контура: Q=150; ρ = 2,5 кОм.

Решение.

1. Для согласования необходимо выпол­нить условие передачи максимально возмож­ной мощности:

.

2. Так как в данной схеме тс = 0, то заданное условие будет выполняться, если

Отсюда

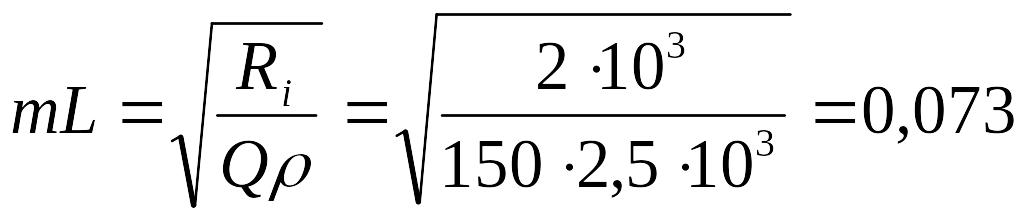
или .