8.2. Комплексные входные и передаточные функции; частотные характеристики

Для описания частотно-избирательных свойств параллельного контура (см. рис. 8.1) наиболее удобны его комплексное входное сопротивление Z(jω) и комплексные передаточные функции по току K₁(jω). Компоненты этих функций определяют входные и переда­точные частотные и резонансные характеристики контура.

Комплексное входное сопротивление является основной харак­теристикой параллельного контура:

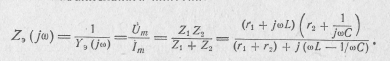
Пренебрегая из-за малости произведением r₁r₂ в числителе и обозначив полное активное сопротивление контура r = r₁ + r₂, на­ходим

где —добротность параллельного контура;

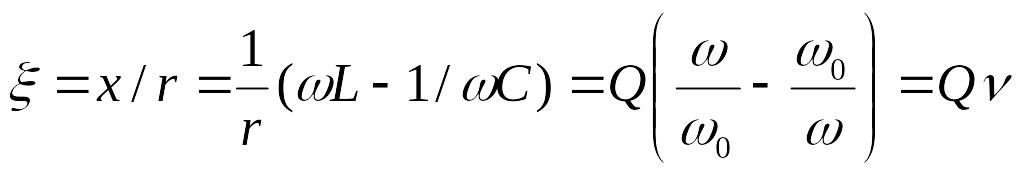— его обобщен­ная расстройка.

Для высокодобротных параллельных колебательных контуров значения ρ, Q, ξ, ν, δ, ω₀ совпадают с их значениями для последо­вательных контуров.

При резонансе, когда ξ=0, эквивалентное сопротивление па­раллельного колебательного контура имеет резистивный характер:

и в Q² раз больше активного сопротивления г.

Таким образом, для комплексного входного сопротивления контура получаем

или после нормирования

Зависимость модуля входного сопротивления параллельного колебательного контура от частоты называется его амплитудно-частотной характеристикой (АЧХ)

Зависимость аргумента входного сопротивления контура от частоты называется его фазо-частотной характеристикой (ФЧХ)

. (8.9)

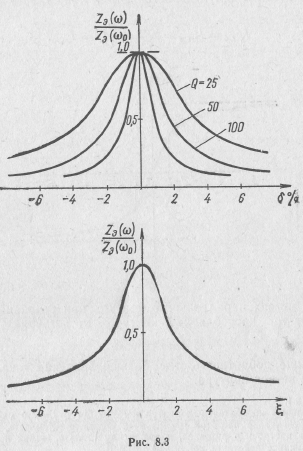
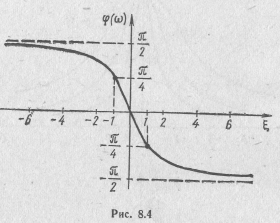
Нормированные АЧХ параллельного (рис. 8.3) и последова­тельного (см. рис. 7.7 и 7.8) контуров совпадают, а их фазо-частотные характеристики отличаются лишь знаком (рис. 7.8 и 8.4). В отличие от последовательного контура параллельный контур на частотах ниже резонансной носит индуктивный харак­тер, а на частотах выше резонансной — емкостной.

Анализ полученных соотношений и характеристик показывает, что при резонансе (ξ==0) ток, потребляемый контуром, очень мал:

(8.10)

В то же время, так как

и т.е.

ток I_mL0 в ветви с индуктивностью равен току I_mC0 в ветви с ем­костью

(8.10)

Токи в ветвях параллельного контура при резонансе в Q раз превышают ток, потребляемый контуром от источника:

. (8.12)

Чем выше добротность, тем больше значение тока, циркули­рующего в ветвях контура.

Пример 8.1.

Параллельный колебательный контур с r=10 Ом и L=230 мкг подключен к источнику сигнала с частотой f₀=465 кГц. Определить емкость, при которой контур будет настроен в резонанс, и амплитуду токов в ветвях при резонансе если при резонансе действует напряжение 120 В.

Решение.

1. Так как , контур будет настроен в резонанс при

пФ.

2. Добротность контура:

3. Ток, потребляемый контуром от источника;

4. Ток в ветвях контура при резонансе:

B реальных радиотехнических цепях параллельный контур ра­ботает от источника с конечным внутренним сопротивлением, на­пример в анодной цепи радиолампы. Эквивалентные схемы такого включения контура приведены на рис. 8.5. B таких схемах нали-

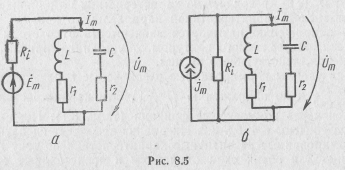
чие конечного внутреннего сопротивления источника R_i не позво­ляет обеспечить режим работы контура с заданным током или заданным напряжением. Значения тока, потребляемого контуром, и напряжения на нем в этих цепях связаны между собой и оказы­вают взаимное влияние.

Поэтому на практике для описания частотно-избирательных свойств параллельного контура нашли применение его частотные и резонансные характеристики с учетом внутреннего сопротивле­ния источника R_i. Практический интерес для расчетов представ­ляют эквивалентные схемы двух видов: с источником э. д. с. (рис. 8.5, α) и с источником тока (рис. 8.5,6). Установим связь между комплексными функциями этих схем.

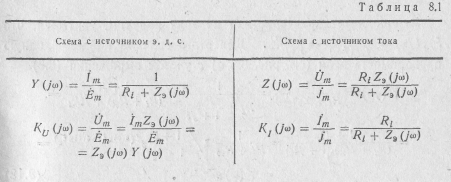
Выражения для комплексных функций обеих Схем легко уста­новить, они приведены в табл. 8.1. Модули и аргументы этих функций являются разновидностями АЧХ и ФЧХ исследуемых це-

пей. Все приведенные функции определяются эквивалентным со­противлением контура Z_э(j) и внутренним сопротивлением источ­ника r_i.

В зависимости от режима работы контура, т. е. от того, что является выходной величиной (ток, потребляемый от источника, или напряжение, действующее на контуре), различают два вида резонансных характеристик: I_т(ω)—резонансную характеристику по току; U_m(ω) —резонансную характеристику по напряжению.

Резонансной характеристикой параллельного контура по току или по напряжению называется зависимость от частоты ампли­туды тока, потребляемого контуром от источника, или амплитуды напряжения, действующего на нем.

Очень удобны нормированные резонансные характеристики: по току и по напряжению . Эти характеристики опре­деляются через комплексные функции (табл. 8.1). Нужные соотношения сведены в табл. 8.2. Их анализ позволяет сделать вывод, что нормированные резонансные характеристики по току и по на­пряжению для обеих схем одинаковы и представляют собой не что иное, как их нормированные входные и передаточные комплексные функции.

Резонансные характеристики по току получим, учитывая, что . Для этого сначала найдем входную проводимость цепи (см. рис. 8.5, а) с учетом выражения (8.6),

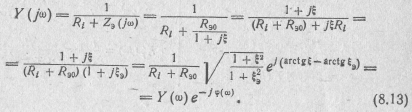
Здесь

эквивалентная обобщенная расстройка;

эквивалентная добротность параллельного контура (g=1/ρ)..

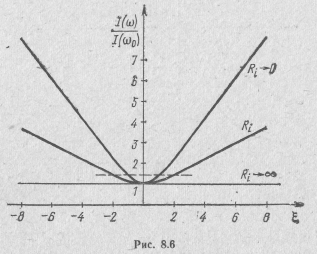
Эквивалентная добротность Q₃ учитывает влияние внутреннего сопротивления источника на резонансные свойства колебательной системы.

После нормирования из формулы (8.13) находим

Модуль этого выражения представляет нормированную резо­нансную характеристику параллельного контура по току:

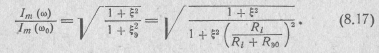
Резонансные кривые по току (рис. 8.6) тем острее, чем меньше внутреннее сопротивление источника. Объясняется это тем, что при малом внутреннем сопротивлении источника параллельный контур работает практически в режиме заданного напряжения. При этом ток, потребляемый от источника, определяется в основ­ном эквивалентным сопротивлением Z_э(jω), а напряжение на кон­туре изменяется слабо. При большом R_i, полное сопротивление цепи дополняется внутренним сопротивлением источника и парал­лельный контур работает практически в режиме заданного тока. Ток, потребляемый контуром в этом случае, определяется в основ-

ном сопротивлением R_i, слабо зависит от сопротивления контура Z_э(jω) и поэтому остается почти неизменным. В этом случае гово­рят о дополняющем действии внутреннего сопротивления R_i источ­ника сигнала на контур.

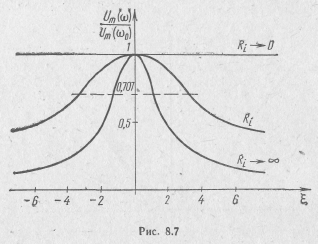
Резонансные характеристики по напряжению находим с по­мощью выражений (8.6), (8.13) и соотношений, приведенных в табл. 8.1:

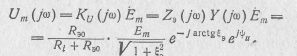
Отсюда

или после нормирования

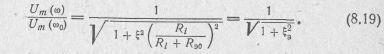
В отличие от резонансных кривых по току резонансные кривые по напряжению параллельного контура тем острее, чем больше внутреннее сопротивление R_i источника (рис. 8.7). Это объясясняется шунтирующим действием сопротивления R_i на контур. Будучи включенным параллельно контуру, оно снижает эквивалентную добротность Q_э и делает резонансные кривые более поло­гими. Чем меньше R_i по сравнению с R_э0, тем меньше напряже­ние на контуре зависит от его входного сопротивления Z_э(ω), тем сильнее сопротивление источника шунтирует контур.

Из резонансных характеристик (см. рис. 8.6 и 8.7) следует, что о настройке параллельного колебательного контура в резонанс можно судить по минимуму потребляемого им тока и по макси­муму действующего на нем напря­жения.

С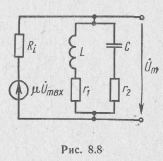 ледует заметить, что напряжение на параллельном контуре (8.18) всегда меньше э. д. с. источника сигнала. Этим, в частности, он отличается от последовательного контура, на выходе которого при резонансе действует на­пряжение, значительно превышающее э.д. с. источника. Параллельный резо­нансный контур в отличие от последо­вательного не может быть использо­ван как усилитель колебаний.

Пример 8.2.

С помощью эквивалентной схемы (рис. 8.8) лампового усилителя высоко­частотного сигнала определить его коэффициент усиления и напряжение на вы­ходе, если известны параметры контура: L=120 мкГ; Q=100; f₀=l,5 МГц; электронной лампы: R = 800 кОм; S = 2 ма/В; μ=1600 и амплитуда выходного сигнала U_{m вх}=30 мкВ.

Решение.

1. Эквивалентное сопротивление параллельного контура при резонансе:

кОм

2. Амплитуда эквивалентной э. д. с. источника в схеме:

мВ

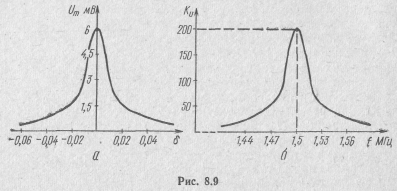
3. Резонансная характеристика по напряжению (рис. 8.9, а):

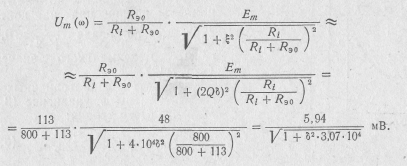
При резонансе на выходе каскада действует напряжение U_m = U_m (ω) = 5,94 мВ.

4. Коэффициент усиления каскада в функции частоты (рис. 8.9,6):

При резонансе коэффициент усиления по напряжению

K_U =K_U(ω) = 198.