7.4. Особенности применения последовательных колебательных контуров

Одним из основных применений последовательного колебатель­ного контура в радиоустройствах является его использование в качестве избирательной резонансной системы. Примером может

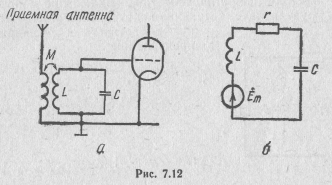
служить входная цепь радиоприемного устройства (рис. 7.12, а). Выходной сигнал в ней снимается с емкости, а входной наводится в контуре за счет магнитной связи с антенной. При этом э. д. с, входного сигнала оказывается включенной последовательно с эле­ментами контура (рис. 7.12,б). Поэтому данный контур является последовательным.

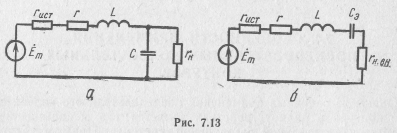
Входное сопротивление усилительного каскада является на­грузкой по отношению к контуру и шунтирует выход контура. Учитывая внутреннее сопротивление источника сигнала r_ИСТ, можно составить эквивалентную схему (рис. 7.13,а). Заменив в ней па­раллельное соединение емкости С и сопротивления нагрузки r_н на эквивалентное ей последовательное соединение емкости С_э и вно­симого сопротивления нагрузки r_н.вн, получим эквивалентный по­следовательный контур (рис. 7.13,6). В нем

,

где

и

Обычно выбирают r_н>>x_c. Поэтому , т. е. . Чем больше значение r_H, тем меньше шунтируется выход контура и тем

м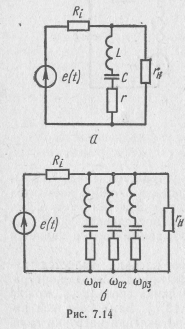 еньше вносимое сопротивление r_н.вн. Включение сопротивлений r_ист и r_н.вн увеличивает затухание контура, снижая его эквивалент­ную добротность и расширяя полосу пропускания:

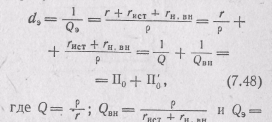
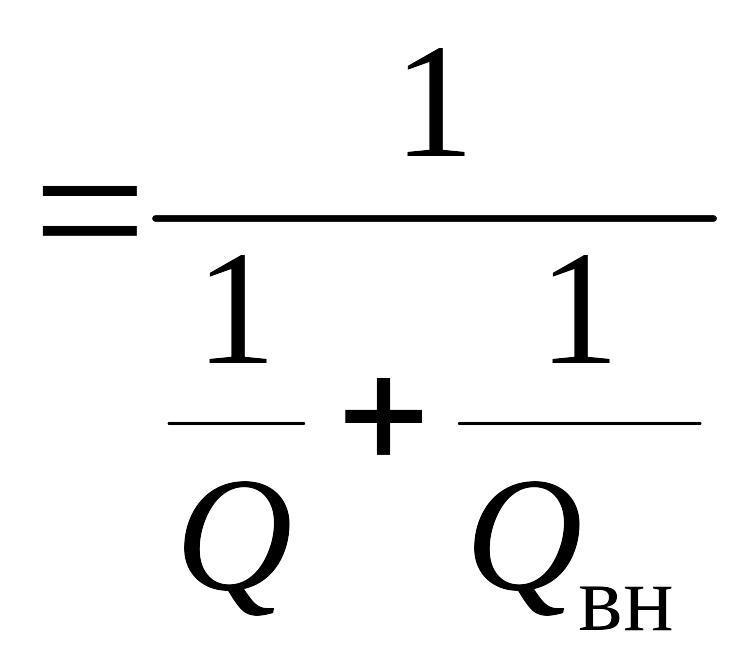- соответственно собственная, внешняя и эквивалентная, или нагруженная, добротность.

В результате снижаются избира­тельные свойства контура. Чтобы этого не происходило, последователь­ный колебательный контур должен работать от источника с малым внут­ренним сопротивлением и на нагрузку, практически не шунтирующую его выход, т. е. вносящую в контур слабые потери.

Колебательный контур является нагрузкой для источника сиг? нала. При настройке в резонанс в нагрузку будет передана мак­симальная мощность сигнала при условии .

Другим примером применения последовательного колебатель­ного контура может служить схема фильтрации, в которой

контур шунтирует нагрузку на частоте подавляемой гармоники (рис. 7.14, а). Для этого он настраивается на частоту данной гар­моники. Шунтирование тем более эффективно, чем меньше актив­ное сопротивление контура по сравнению с сопротивлением на­грузки на данной частоте. Для подавления ряда гармоник парал­лельно нагрузке включаются несколько резонансных контуров (рис. 7.14,6), каждый из которых настраивается на частоту соот­ветствующей гармоники. Подобные схемы широко используются и в электротехнических силовых устройствах в качестве фильтров. В приведенных на рис. 7.14 схемах колебательный контур вклю­чается параллельно нагрузке и работает более эффективно от источника с большим внутренним сопротивлением.

8. Параллельный колебательный контур

8.1. Условие резонанса и резонансная частота

Параллельным колебательным контуром называется цепь, со­стоящая из параллельного соединения ветви с индуктивностью и ветви с емкостью (рис. 8.1). Потери в этих ветвях учитываются сопротивлениями r₁ и r₂.

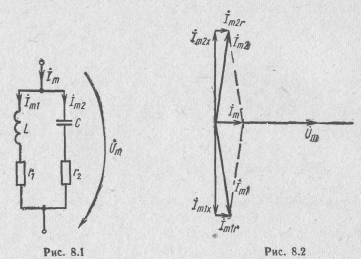
В параллельном колебательном контуре может возникать ре­зонанс токов, т. е. явление, при котором токи в реактивных эле­ментах значительно превышают ток, потребляемый контуром от источника.

Это является следствием того, что при резонансе сдвиг фаз между токами и в параллельных ветвях контура близок к 180° (в идеальном контуре с r₁ = r₂ = 0 сдвиг фаз равен 180°). Поэтому результирующий ток оказывается по величине очень мал (рис. 8.2),

Резонанс токов наступает, когда реактивные составляющие этих токов взаимно компенсируются, а ток , потребляемый кон­туром, совпадает по фазе с действующим на контуре напряже­нием . Сопротивление параллельного контура при резонансе становится активным.

Реактивные составляющие токов и прямо пропорцио­нальны реактивным проводимостям b_L и b_с ветвей контура. По­этому условием резонанса токов в параллельном колебательном контуре является равенство нулю¹ его реактивной проводимости:

b_p=b_Lp+b_Cp=0. (^8J)

Здесь b_p, b_Lp, b_Cp — реактивные проводимости контура и его ветвей при резонансе (ω = ω₀).

Выражая реактивные проводимости ветвей через их реактаные сопротивления, из выражения (8.1) получим

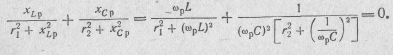
Отсюда, учитывая выражения (7.2) и (7.4), находим резонанс­ную частоту параллельного контура

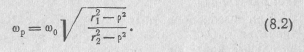
Анализируя полученное выражение, приходим к выводу, что резонанс токов в параллельном контуре возможен, еслиr₁ и r₂>ρ или r₁ и r₂<ρ.

Резонансная частота параллельного контура в общем случае отличается от ω₀. Однако в высокодобротных радиотехнических контурах

(8.3)

Ниже ограничимся рассмотрением лишь высокодобротных па­раллельных контуров, для которых условие резонанса токов прак­тически совпадает с условием резонанса напряжений в последова­тельных колебательных контурах.