
- •6.5. Расчет комплексных функций цепи с помощью матриц ее контурных сопротивлений и узловых проводимостей
- •7.2. Комплексные входные и передаточные функции; частотные характеристики
- •7.3. Полоса пропускания, понятие об избирательности, коэффициент прямоугольности
- •7.4. Особенности применения последовательных колебательных контуров
- •8. Параллельный колебательный контур
- •8.1. Условие резонанса и резонансная частота
- •8.2. Комплексные входные и передаточные функции; частотные характеристики
- •8.3. Полоса пропускания и коэффициент прямоугольности
- •8.4. Сложные параллельные колебательные контуры
- •8.5. Особенности применения параллельных колебательных контуров
- •9.2. Эквивалентные схемы и комплексные функции системы двух связанных контуров
- •9.З. Резонансы в системе связанных контуров. Частные и сложные резонансы
- •9.4. Частотные характеристики системы связанных колебательных контуров
- •9.5. Полоса пропускания и коэффициент прямоугольности
- •Понятие о многосвязанных колебательных контурах
- •Применение связанных
- •Колебательных контуров
- •10. Основы теории четырехполюсников
- •10.1. Основные понятия и определения
- •10.2. Уравнения, параметры и схемы замещения четырехполюсника
- •10.3. Комплексные входные и передаточные функции четырехполюсника
- •10.4. Характеристические параметры четырехполюсника
- •10.5. Параметры рассеяния четырехполюсника
7.3. Полоса пропускания, понятие об избирательности, коэффициент прямоугольности
Сигнал занимает определенную полосу частот, т. е. наряд; с основной частотой он имеет составляющие и на дополнительных частотах. Колебательный контур должен пропускать всю занимаемую сигналом полосу частот.
Полоса
пропускания колебательного контура,
как и любой другой частотно-избирательной
системы, — понятие условное. Полосы
пропускания последовательного
колебательного контура называется
диапазон частот вблизи резонанса, на
границах которой амплитуда тока в
контуре снижается до уровня:
![]() 0,707
своей максимального значения. Это
соответствует уменьшению вдвое мощности,
выделяемой в контуре. Полоса пропускания
включает
в
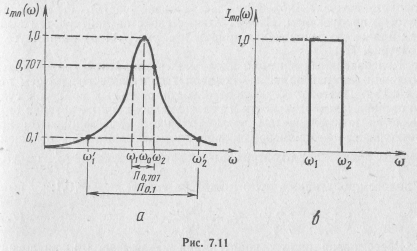
себя частоты от нижней граничной ω1до
верхней граничной ω2
(рис. 7.11,а). Различают абсолютную и
относительную полосы пропускания.
0,707
своей максимального значения. Это
соответствует уменьшению вдвое мощности,
выделяемой в контуре. Полоса пропускания
включает
в
себя частоты от нижней граничной ω1до
верхней граничной ω2
(рис. 7.11,а). Различают абсолютную и
относительную полосы пропускания.
Разность граничных частот
П = ω2-ω1 (7.40)
называется абсолютной полосой пропускания.
Отношение разности граничных частот к резонансной частоте:
![]()
называется относительной полосой пропускания.
Для
нахождения граничных частот подставим
в
уравнение
резонансной кривой (7.29) значение
относительного тока, равное
![]()
![]()
Отсюда следует, что границам полосы пропускания соответствует обобщенная расстройка
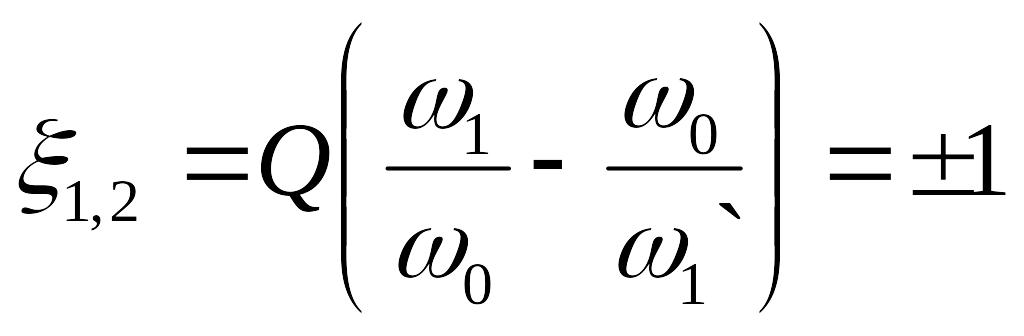 ,
т. е.
,
т. е.
![]()
Решение этого уравнения дает выражения для граничных частот:
![]()
и для полосы пропускания контура:
![]() (7.44)
(7.44)
(7.45)
Таким образом, полоса пропускания колебательного контура определяется его добротностью и обратно пропорциональна ей. Чтобы изменить полосу пропускания контура, необходимо изменить его добротность.
Избирательностью колебательного контура называется его способность выделять колебания в диапазоне частот, ограниченном полосой пропускания. Избирательные свойства контура тем выше, чем ближе его резонансная кривая (см. рис. 7.11,а) к прямоугольной (рис. 7.11,б).
Колебательный
контур с идеальной резонансной кривой
прямоугольной формы полностью
подавляет колебания вне полосы
пропускания. Поэтому об избирательности
реальных контуров судят по степени
прямоугольности их резонансных кривых,
которая определяется коэффициентом
прямоугольности. Коэффициентом
прямоугольности резонансной кривой
контура называется отношение
полосы
пропускания контура, отсчитанной на
уровне -
0,707,
к полосе пропускания, отсчитанной на
уровне
![]()
![]() (7.46)
(7.46)
Рассчитывая полосу пропускания на уровне 0,1 аналогично выражениям (7.42) — (7.45), убеждаемся, что для последовательного колебательного контура коэффициент прямоугольности является постоянной величиной, не зависящей от его параметров:
![]() .
(7.47)
.
(7.47)
Коэффициент
прямоугольности одинаков для всех
последовательных контуров и не
зависит от их добротности. Так как в
идеальном
случае
![]() ,
можно заключить, что избирательность
последовательного контура невысока.
Это ограничивает применение резонансных
контуров такого типа.
,
можно заключить, что избирательность
последовательного контура невысока.
Это ограничивает применение резонансных
контуров такого типа.
Пример 7.3.
Последовательный колебательный контур настроен на частоту f0=1 МГц. Определить добротность, при которой этот контур пропустит полосу частот П=10 кГц.
Решение.
Известно, что
![]() или
или
![]() Гц.
Поэтому
Гц.
Поэтому
![]()
Пример 7.4.
Последовательно в контур с активным сопротивлением r=5 Ом подключено добавочное активное сопротивление rД = 2 Ом. Как изменится полоса пропускания контура?
Решение.
1. Добротность и полоса пропускания контура до включения:
![]() .
.
2, Добротность и полоса пропускания контура после включения:
![]() .
.
3. Полоса пропускания изменится в
![]() раз.
раз.
