7.2. Комплексные входные и передаточные функции; частотные характеристики

Для анализа и описания частотно-избирательных свойств коле­бательных контуров используются комплексные входные и переда­точные функции. Наиболее удобными для последовательных кон­туров являются комплексная входная проводимость Y(jω) и ком­плексные передаточные функции по напряжению K_U(jω). Компо­ненты этих функций определяют частотные и резонансные харак­теристики контура.

Понятия частотных и резонансных характеристик взаимно свя­заны, так же как ток и напряжения в контуре связаны с его ком­плексными функциями. Если частотными характеристиками кон­тура являются зависимости компонентов комплексных функций от частоты, то резонансными характеристиками называют зависи­мость амплитуды тока в контуре или напряжения на его элемен­тах от частоты.

Комплексная входная проводимость последовательного колеба­тельного контура (см. рис. 7.1) легко рассчитывается через его вторичные параметры:

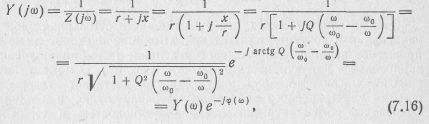
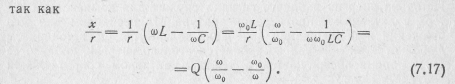
Более удобное выражение получаем после нормирования, от­неся Υ(jω) к его значению при ω = ω₀.

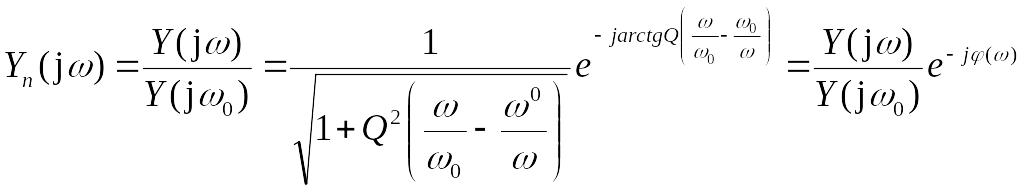(7.18)

Комплексная проводимость контура непосредственно опреде­ляет ток в нем, так как

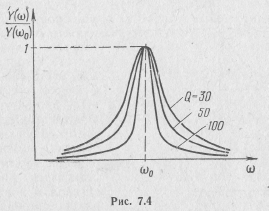
Зависимость полной проводимости последовательного контура Υ(ω) от частоты называется его амплитудно-частотной характери­стикой (АЧХ). Более удобной является нормированная амплитуд­но-частотная характеристика, совпадающая с нормированной резонансной характеристикой:

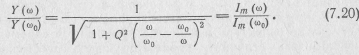
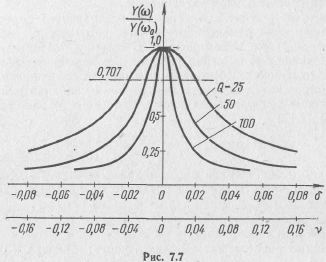
Увеличению добротности контура соответствуют более острые резонансные кривые или усиление его частотно-избирательных свойств (рис. 7.4). При большой добротности резонансные кривые симметричны относительно точки резонанса.

Зависимость аргумента тока в контуре или его проводимости от частоты ω называется фазо-частотной характеристикой (ФЧХ)

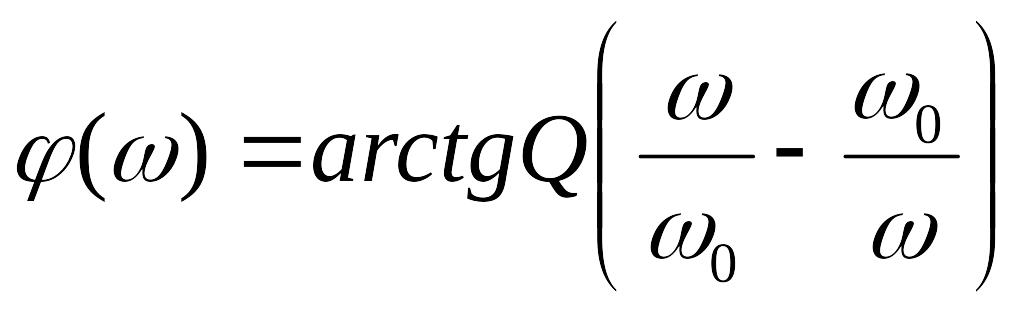(7.21)

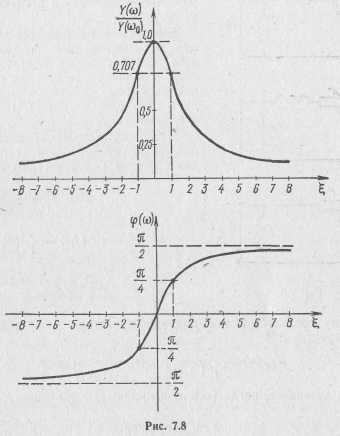
Фазо-частотная характеристика последовательного колебатель­ного контура приведена на рис. 7.5. Из нее следует, что на часто­тах ниже резонансной контур имеет емкостной характер, при ре­зонансе— резистивный, а на частотах выше резонансной — индук­тивный.

Д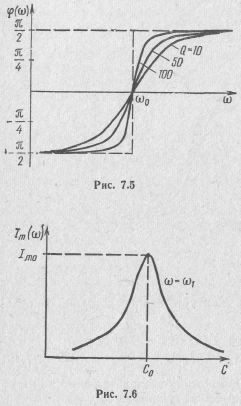 остичь резонанса в кон­туре можно не только изме­нением частоты сигнала (при неизменных параметрах кон­тура), но и настройкой са­мого контура путем измене­ния его емкости или индук­тивности (при неизменной частоте источника). Обычно для настройки контура из­меняется его емкость, для чего в контур включается конденсатор переменной ем­кости. При определенном значении емкости С₀ резо­нансная частота контура ω₀, становится равной частоте сигнала ω и в контуре воз­никает резонанс. Зависи­мость амплитуды тока в кон­туре от значения его емко­сти С или индуктивности L (рис. 7.6) при заданной ча­стоте источника называют настроечной характеристи­кой контура. Вблизи резо­нанса настроечные кривые практически совпадают с ре­зонансными.

В радиотехнике особенно часто применяются колебательные контуры высокой добротности. При этом наибольший интерес пред­ставляет режим контура в диапазоне частот, близких к резонанс­ной. В этом случае при исследовании частотных характеристик ко­лебательного контура в качестве независимой переменной удобно использовать величину, характеризующую расстройку контура, т. е. степень отклонения его резонансной частоты ω₀ от частоты сигнала ω. Такая замена переменных позволяет придать расчет­ным формулам более общий и удобный вид.

Разность между частотой сигнала и резонансной частотой кон­тура

Δω = ω —ω₀ (7.22)

называют абсолютной расстройкой. Она может быть как положи­тельной (ω>ω₀), так и отрицательной (ω< ω₀.).

Отношение абсолютной расстройки к резонансной частоте

(7.23)

называется относительной расстройкой.

Отклонения режима контура от резонансного определяются двумя причинами: изменением частоты источника и изменением параметров контура. С помощью абсолютной и относительной рас­строек оценивают отклонения режима, обусловленные изменением частоты. Отклонения, обусловленные обеими причинами, оцени­вают с помощью обобщенного критерия — отношения реактивного сопротивления контура к активному, равного в соответствии с вы­ражением (7.17)

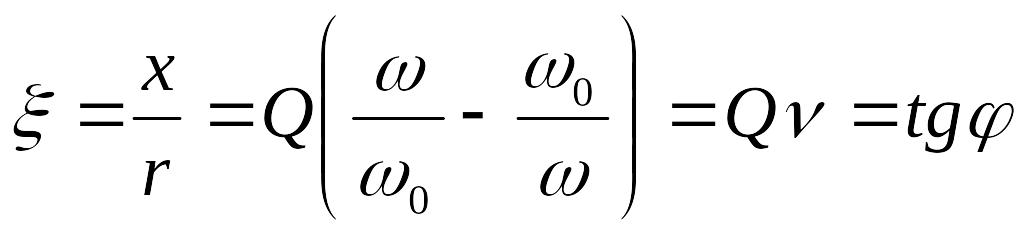(7.24)

и называемого обобщенной расстройкой. Зависимость обобщенной расстройки от частоты сигнала оценивается фактором расстройки

(7.25)

При малых расстройках в области частот, близких к резонанс­ной ( ),

так как . Поэтому вблизи резонанса

(7.26)

и

. (7.27)

Относительная и обобщенная расстройки, как и фактор рас­стройки, — безразмерные величины. Все виды расстроек при резо­нансе (ω = ω₀) равны нулю.

Относительная ошибка при расчетах по приближенной формуле (7.27) имеет значение

(7.28)

Пример 7.2.

На последовательный колебательный контур с параметрами: L=400 мкГ; С=100 пФ; r=5 Ом — поступает сигнал с частотой f=0,8 мгц. Определить абсолютную, относительную и обобщенную расстройки контура.

Решение.

1. Резонансная частота контура

2. Добротность контура:

3. Расстройки контура:

абсолютная

рад/с;

относительная

обобщенная

Подставляя выражения (7.24) — (7.27) в формулы (7.2О), (7.21), получим выражения нормированных частотных характери­стик контура в функции расстройки:

(7.29)

φ (ω) = arctg Qν = arctg ξ (7.30)

или то же для области малых расстроек:

(7.31)

, (7.32)

Соответствующие этим выражениям графики приведены на рис. 7.7 и 7.8. Частотные характеристики являются симметричными

кривыми. Кривые, построенные по приближенным формулам, дают хорошее совпадение для малых расстроек, когда , что вполне достаточно для описания частот-

но-избирательных свойств радиотехнических колебательных кон­туров.

Частотные характеристики, построенные для последовательных контуров в функции относительной расстройки δ или фактора рас­стройки v, совпадают, когда добротности контуров одинаковы. Если в качестве независимой переменной выбрать обобщенную расстройку, то частотные характеристики, построенные для любого последовательного колебательного контура, полностью совпадут. Такие зависимости (см. рис. 7.8) называют обобщенными частот­ными характеристиками. Они описывают частотно-избирательные свойства всех без исключения колебательных контуров данного типа. Обобщенные характеристики не позволяют непосредственно

оценить влияние параметров контура на форму его резонансных кривых, но они очень удобны при сравнении контуров разного типа, например последовательных с параллельными или с систе­мой связанных контуров и т. п. Ис­пользование обобщенной расстройки упрощает уравнения и расчетные фор­мулы.

К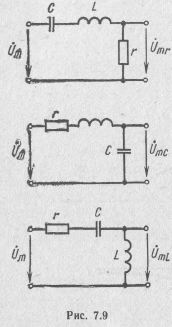 омплексные передаточные функ­ции по напряжению последователь­ного колебательного контура разли­чают в зависимости от того, напряже­ние на каком из его элементов яв­ляется выходным (рис. 7.9). Найдем эти функции.

Для передаточной функции по на­пряжению на активном сопротивле­нии с учетом (7.29) и (7.30) получаем

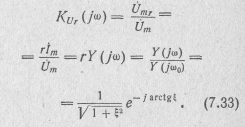
Этому соответствуют амплитудно-частотная и фазо-частотная характеристики:

При резонансе, когда ξ=0, они принимают значения: K_Ur(ω₀) =1; φ_r(ω₀) = 0.

Передаточная функция по напряжению на емкости

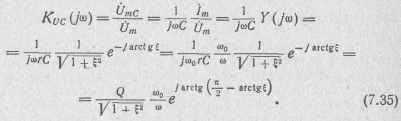
Ей соответствуют частотные характеристики:

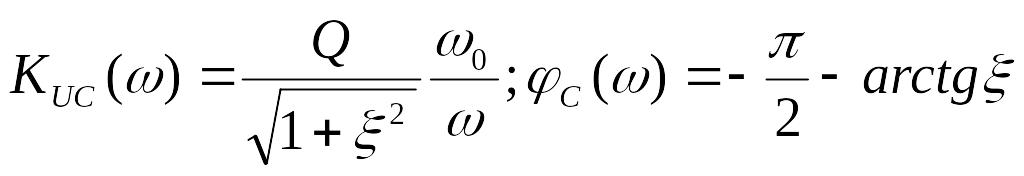. (7.36)

Их значения при резонансе:

.

Для передаточной функции по напряжению на индуктивности

находим

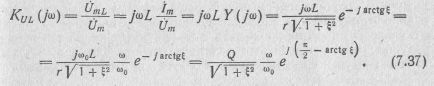
Частотные характеристики в этом случае:

. (7.38)

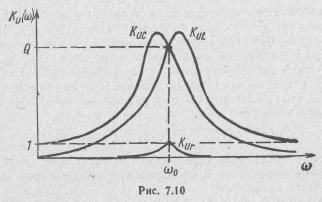
При резонансе они имеют значения К_UL(ω₀) = Q и φ(ω₀) = π/2. Графики соответствующих характеристик приведены на рис. 7.10. Численно передаточные функции, или коэффициенты пе­редачи по напряжению, показывают, во сколько раз напряжение на соответствующем элементе больше напряжения, действующего на входе контура. Из полученных соотношений, в частности, сле­дует, что при резонансе напряжения на реактивных элементах в Q раз превышают входное напряжение, а напряжение на актив­ном сопротивлении равно ему.

Интересно, что напряжения на реактивных элементах дости­гают своего максимального значения в стороне от резонанса. Ис­следования функций К_UC(ω) и К_UL(ω) на экстремум показывают, что максимума они достигают на частотах:

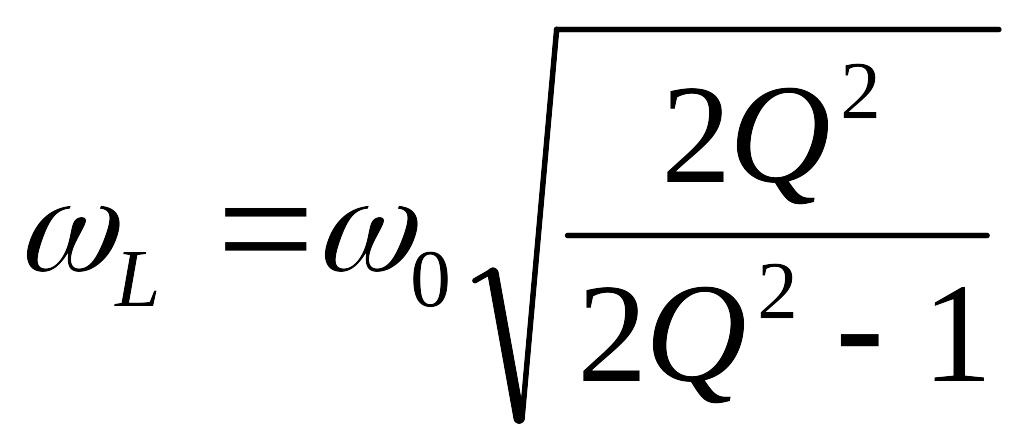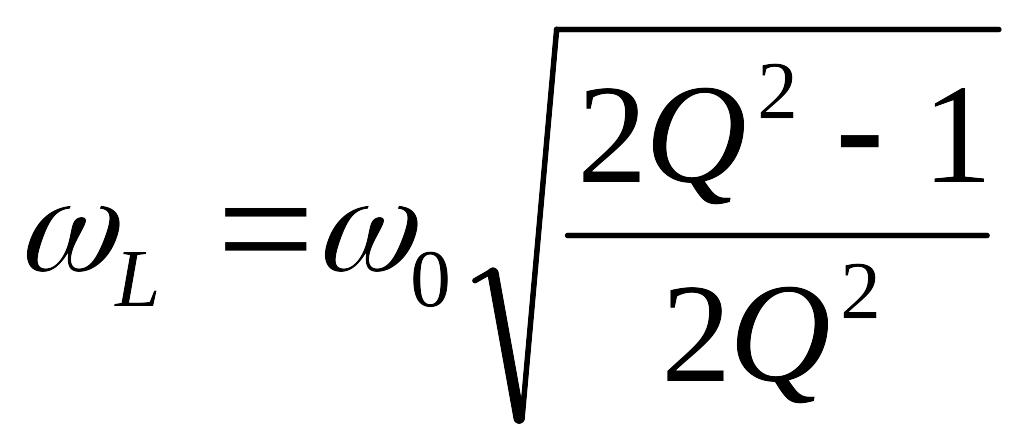и . (7.39)

Максимальные значения этих функций одинаковы:

.

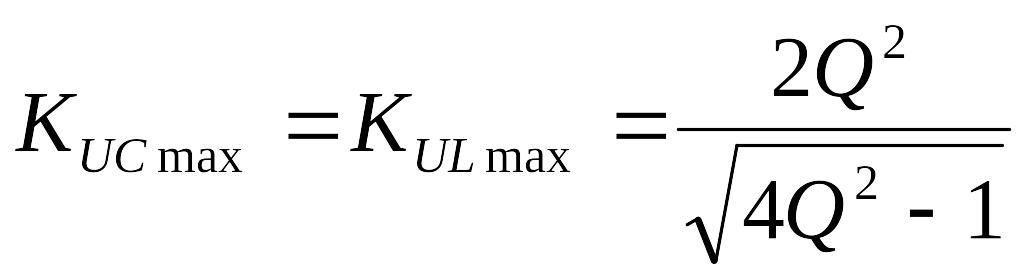Из приведенных частотных характеристик (см. рис. 7.10) лишь К_ur(ω) имеет экстремум при резонансе. Поэтому о настройке последовательного контура в резонанс можно судить по максимуму напряжения на активном сопротивлении или тока в нем. Степень смещения ω_L, и ω_с относительно резонансной частоты шо опреде ляется добротностью контура. Например, уже при Q=10 получаегу ω_L = 1,01 ω₀, a ω_с =0,99 ω₀. Поэтому для высокодобротных контуров можно считать

и

что позволяет достаточно точно судить о настройке высокодобротных контуров в резонанс и по максимуму напряжения на любом из реактивных элементов.

Из всех комплексных коэффициентов передачи последовательного контура практический интерес представляет передаточная; функция по напряжению на емкости Kuc(ω)· Объясняется это тем что в реальном контуре его активное сопротивление определяете активным сопротивлением индуктивной катушки, в частности провода, который на ней намотан. Измерить же напряжение на индуктивности практически нельзя, так как активное сопротивление катушки нельзя отделить от ее индуктивности. Обычно выходное, напряжение в последовательном контуре снимается с емкости.