10.5. Параметры рассеяния четырехполюсника

Общепринятые параметры четырехполюсника в целом ряде случаев являются неудобными. Многие схемы не могут быть опи­саны с их помощью. С другой стороны, на частотах выше 100—200 МГц осуществление холостого хода и короткого замыкания при измерениях параметров четырехполюсника вызывает серьез­ные трудности. Этих недостатков лишен волновой подход к опи­санию четырехполюсников. Сейчас он приобретает особый интерес для анализа транзисторных схем на сверхвысоких частотах (СВЧ). В его основе лежат соотношения так называемых падающих и от­раженных волн напряжений, токов или мощностей.

По аналогии с явлением отражения электромагнитных волн от поверхностей раздела сред параметры, описывающие отражение и поглощение потоков мощности на зажимах многополюсника, на­зывают волновыми параметрами или параметрами рассеяния. Их удается измерить до частот порядка 12 ГГц.

С параметрами рассеяния связаны две важные операции: нор­мирование величин и определение переменных рассеяния. Норми­рование напряжений и токов, действующих, например, на зажимах двухполюсника, соответствует включению идеального нормирую­щего трансформатора с коэффициентом трансформации

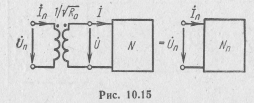
как это показано на рис. 10.15. Оно осуществляется следующим способом:

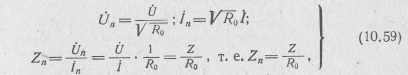
где R₀ — базисное сопротивление или сопротивление нормирования. Значение этого сопротивления может быть выбрано произвольным, однако обычно выбирается с учетом параметров внешней цепи, например равным внутреннему сопротивлению источника или вол­новому сопротивлению соединительного волновода, что упрощает расчеты.

Переменные рассеяния представляют линейные комбинации нормированных напряжений и токов и определяются как их полу­сумма и полуразность:

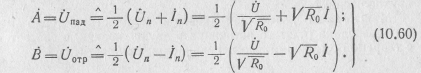
Эти величины называют соответственно падающей и отражен­ной волнами нормированного напряжения. Следует заметить, что квадрат их модуля имеет размерность мощности.

Складывая и вычитая переменные рассеяния, можно выразить напряжение и ток, действующие в цепи:

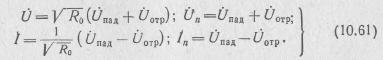
Падающую волну на входе произвольного двухполюсника можно всегда выразить через параметры источника з. д. с. Е_вх с внутренним активным сопротивлением z_bh=R₀. считая его подключенным к зажимам двухполюсника. Представляя двухполюс-

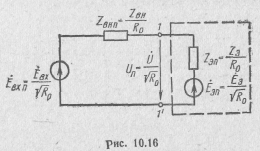
ник эквивалентным генератором с внутренним сопротивлением Z_э э.д. с. Е_э (рис. 10.16), получаем

Отсюда находим

Если выбрать т. е. , то

(10.62)

Таким образом, если к двухполюснику подключить источник с внутренним сопротивлением Z_BH=R₀, то падающая волна , на его зажимах будет равна половине нормированной э.д.с, источника и совершенно не будет зависеть от параметров двухполюсника.

Максимально возможная активная мощность, которая может быть передана от этого источника в двухполюсник, в соответствии с теоремой о максимально передаваемой мощности

т. е. равна квадрату модуля падающей волны.

Мощность, рассеиваемую в пассивной цепи, можно выразить через переменные рассеяния:

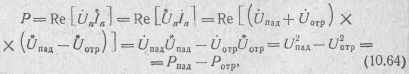
так как

.

Рассеиваемая в цепи мощность выражается разностью двух составляющих: падающей и отраженной мощности. Когда Р_отр=0, отражение отсутствует и цепь потребляет всю максимально воз­можную мощность Р = Р_пад = U²_пад.

Для описания двухполюсника достаточно одного параметра. Отношение отраженной волны нормированного напряжения на за­жимах двухполюсника к падающей волне называется его коэф­фициентом рассеяния или отражения:

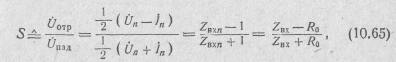
где -нормированное входное или внутреннее сопротивление двухполюсника.

Коэффициент отражения двухполюсника является мерой откло­нения значения его входного сопротивления от оптимального, ко­торое определяется условием передачи максимума мощности от источника с внутренним активным сопротивлением R₀ в данный двухполюсник.

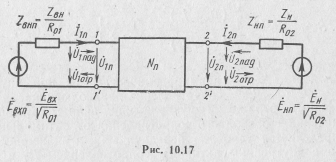
Для четырехполюсника характерно наличие двух систем пере­менных рассеяния: и на первичной стороне и , и на вторичной (рис. 10.17):

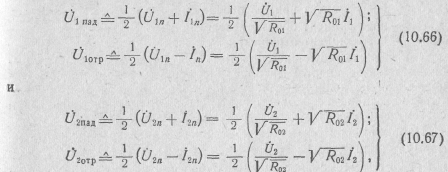
где R₀₁, R₀₂— сопротивления нормирования.

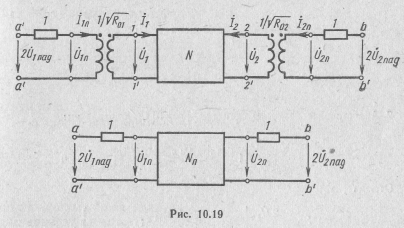
Если в качестве независимых переменных выбрать падающие волны, а в качестве зависимых — отраженные, то для четырехпо­люсника можно записать систему волновых уравнений:

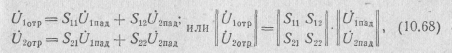
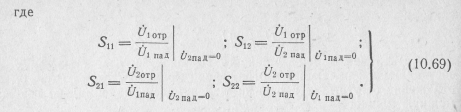
Здесь — матрица рассеяния четырехполюсника, элементы которой являются его параметрами рассеяния,

Физический смысл S-параметров ясен из формул (10.69), Исходя из него, параметры получили названия:

S₁₁ — коэффициент отражения на входе;

S₂₁ — коэффициент прямой передачи;

S₁₂ — коэффициент обратной передачи;

S₂₂ — коэффициент отражения на выходе.

Так как нормирующие сопротивления R₀₁ и R₀₂ могут быть вы­браны произвольно, то матрица рассеяния для данного четырех­полюсника не является единственной. Поэтому для описания че­тырехполюсника необходимо знать его матрицу рассеяния ||S|| и систему выбранных базисных величин R₀₁ и R₀₂.

Параметры рассеяния четырехполюсника легко определить из формул (l·0.69). Для этого уясним смысл условий и . Рассматривая четырехполюсник на рис. 10.17 относительно зажимов 1—1´ как двухполюсник, с помощью выражения (10.62) устанавливаем, что равенству соответствует усло­вие согласования на входе Z_BHn=l при . Отмечая, что на вторичной стороне падающая волна по отношению к двух­полюснику, которым является нагрузка, представляет отражен­ную волну, аналогично установим, что равенству соот­ветствует условие согласования на выходе при .

Коэффициенты отражения четырехполюсника находим, исполь­зуя формулы (10.66) и (10.67):

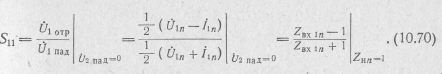
Здесь — входное сопротивление нормированного четырехполюсника, нагруженного на единичное сопротивление, т. е. в режиме согласования на выходе.

Нормирование четырехполюсника осуществляется включением с обеих его сторон нормирующих трансформаторов с коэффициен­тами трансформации и если их внешние обмотки считать первичными.

Аналогично

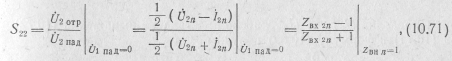
где - выходное сопротивление нормированного четырехполюсника, нагруженного со стороны 1—1' на единичное сопротивление, т. е. в режиме согласования на входе.

Коэффициент отражения S_jj на j-й стороне четырехполюс­ника— это мера отклонения ее режима от оптимального, который определяется условием потребления максимума мощности от источника с внутренним сопротивлением, равным ее базисному сопротивлению R₀j, если на противоположной i-й стороне четырех­полюсник нагружен на соответствующее ей базисное сопротивле­ние R_0i.

Коэффициенты передачи четырехполюсника находим с по­мощью выражения (10.69). Для этого в схеме рис. 10.17 сначала примем и , что соответствует условию согласования на выходе . В этом случае в соответствии с равенством получим

. (10.72)

Формула (10.69) для S₂₁ не содержит . Поэтому коэффициент S₂₁. может быть найден при произвольном значении .

В рассматриваемом случае, учитывая (10.61) и (10.70), на­ходим

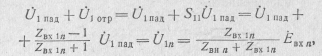
откуда

Удобно выбрать , что в нашей схеме возможно при , чему соответствует .

Для определения коэффициента S₂₁ падающую волну выбирают такой, какой она была бы в режиме согласования на входе ( ). т. е. в соответствии с равенством (10.62):

Определив Ù_2oTp и ^_пад,после подстановки выражений (10.72) и (10.74) в формулу (10.69) получим

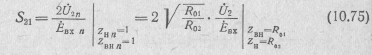
Совершенно аналогично при =0, чему соответствует и , находят коэффициент обратной передачи:

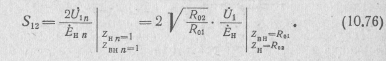
Сравнивая полученные выражения для волновых коэффициен­тов передачи S₂₁ и S₁₂ с формулой (10.34), можно установить, что каждый из них равен удвоенному нормированному рабочему коэффициенту передачи четырехполюсника по напряжению в пря­мом или обратном направлении при условии и .

В общем случае волновой коэффициент передачи S_ji четырех­полюсника N — это удвоенная передаточная функция по напряже­нию нормированного четырехполюсника N_n, дополненного единич­ным активным сопротивлением с одной стороны и нагруженного таким же сопротивлением с другой стороны (рис. 10.18), т. е. в режиме согласования на входе и выходе.

Нормированный четырехполюсник становится дополненным, если подключить последовательно каждому из его входов единич-

ное активное сопротивление (рис. 10.19). Параметры рассеяния представляют, по сути, параметры короткого замыкания норми­рованного и дополненного четырехполюсника. Но характеризуют

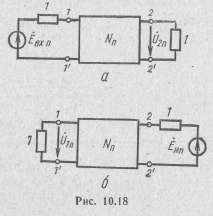
они данный четырехполюсник без предварительного нормирова­ния и дополнения.

Пример 10.7.

Найти матрицу рассеяния идеального трансформатора. Решение.

1. Поочередно замыкая зажимы нормированного и дополненного идеаль­ного трансформатора (рис. 10.20), находим:

где — нормированный коэффициент трансформации.

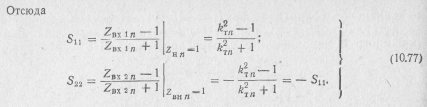
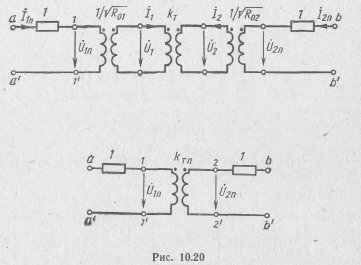
2. Аналогично с помощью схем (см. рис. 10.18) определяем:

Отсюда

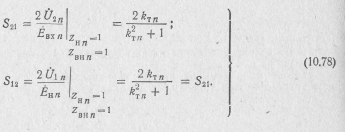
Все S-параметры безразмерны. Для взаимных четырехполюс­ников выполняется равенство S₂₁=S₁₂ указывающее на равен­ство условий передачи в обоих направлениях, т. е. взаимный че­тырехполюсник является обратимым,

200