10.4. Характеристические параметры четырехполюсника

Анализ линий связи, линий задержки, фильтров и других слож­ных четырехполюсников часто основан на их представлении в виде каскадного соединения ряда простых четырехполюсников. Для описания таких схем оказывается удобным использование харак­теристических параметров. Характеристические параметры объеди­няют два вида функций: характеристические сопротивления z_c1. и Z_C2, характеризующие четырехполюсник с одной стороны (1—1' или 2—2'), и характеристический коэффициент передачи у, харак­теризующий соотношение напряжений и токов на входе и выходе четырехполюсника, т. е. его свойства передачи.

Характеристические параметры используются для описания взаимных четырехполюсников. Можно эти параметры определить и для невзаимного четырехполюсника, но в таких случаях харак­теристические параметры не применяются.

Рассмотрим четырехполюсник, показанный на рис. 10.2. Наи­более благоприятным режимом передачи сигнала через него яв-

¹ Конвертором отрицательного иммитанса называется четырехполюсник, описываемый уравнениями:

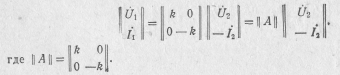
ляется согласованный режим работы, когда ---вн=---.β...• и

Zl·l ⁼ ·-·-BblX·

Первое условие обеспечивает согласование на входе, а вто­рое — согласование на выходе. При выполнении этих условий пол­ная мощность в нагрузке достигает своего максимума и, что более важно, отсутствуют искажения сигнала. Входные сопротивления Z_BX и Z_nix являются функцией сопротивлений Z_H и Z_BH соответ­ственно.

Характеристическими сопротивлениями называются такие со­противления, которые, будучи взяты в качестве Z_H и Z_BH, обеспечи­вают выполнение условий согласования:

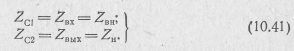
Подставляя выражения (10.30) и (10.31) в эти равенства, с помощью формул, приведенных в табл. 10.1, найдем

и (10.42)

или с учетом формулы (10.23)

и . (10.43)

Для симметричных четырехполюсников

. (10.44)

Характеристическое сопротивление Zc является средним гео­метрическим сопротивлений Z_X и Z_K.

Во всех формулах для Z_C1. и Z_C2 перед корнем взят знак «плюс», так как они являются сопротивлениями пассивных цепей и поэтому не могут иметь отрицательную вещественную часть.

Таким образом, если внутреннее сопротивление источника сиг­нала и сопротивление нагрузки выбрать равными соответствую­щим характеристическим сопротивлениям четырехполюсника, то он будет работать в согласованном режиме.

Характеристический коэффициент передачи γ четырехполюсника определяют с помощью соотношения, записанного аналогично вы­ражению (6.35) в экспоненциальной форме:

. (10.45)

Подставляя в него выражения (10.32) и (10.33), после логариф­мирования получим

(10.46)

В согласованном режиме, когда ,

(10.47)

так как

,

Используя формулы, по которым логарифмы выражаются че­рез гиперболические функции ', можно записать

(10.48)

Пример 10.6

Найти характеристические параметры Т-образной симметричной схемы

(рис. 10.14).

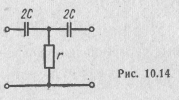
Решение.

Для Т-схемы находим

Поэтому

. (10.49)

В согласованном режиме

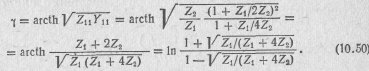
¹ Главные значения обратных гиперболических функций выражаются через логарифмы формулами:

Характеристический коэффициент передачи в общем случае является комплексным числом и имеет вещественную и мнимую части;

. (10.51)

Здесь α—-собственное затухание четырехполюсника, ß — коэф­фициент фазы.

Чтобы выяснить смысл этих компонентов, выразим комплекс­ные передаточные функции четырехполюсника через его характе­ристические параметры. Из формулы (10.45) следует

и (10.52)

так как в согласованном режиме

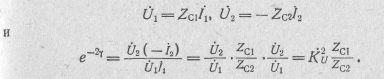
Заметим, что

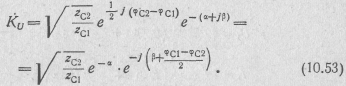
Выражение для К, можно получить в аналогичном виде.

Отсюда следует, что отношение амплитуд напряжения (тока) на выходе и входе четырехполюсника определяется его собствен­ным затуханием α и соотношением модулей характеристических сопротивлений. Сдвиг фаз между напряжениями (токами) на вы­ходе и входе определяется коэффициентом фазы четырехполюс­ника ß и полуразностью аргументов его характеристических сопро­тивлений.

В симметричных четырехполюсниках Z_С1 = Z_С2, т. е. отношения амплитуд напряжений и токов на выходе и входе и их фазовые сдвиги полностью определяются соответственно коэффициентами α и ß:

. (10.54)

Недостатком характеристических параметров, снижающим в ряде случаев их ценность, является наличие в полученных выра­жениях корня квадратного. Характеристические сопротивления, представленные иррациональными выражениями, не могут быть реализованы конечным числом элементов. Цепи, состоящие из ко­нечного числа элементов, всегда имеют сопротивление, выражае­мое рациональной функцией, Поэтому решение задач синтеза с по-

мощью характеристических параметров возможно лишь прибли­женно.

Используя характеристические параметры, уравнения четырехполюсника можно записать в виде, удобном для описания цепей с распределенными па­раметрами. Для этого следует А-нараметры выразить через характеристические параметры.

С помощью формул преобразования (табл. 10.1) находим:

(10.55)

; т. e. . (10.56)

Отсюда

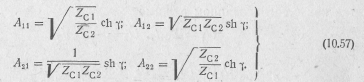
Используя уравнения четырехполюсника (10.17) в Л-форме, с помощью выражений (10.57) получаем уравнения четырехполюсника в гиперболических функциях:

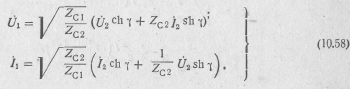
Уравнения такого вида играют важную роль при анализе процессов в длин­ных однородных линиях.