10.3. Комплексные входные и передаточные функции четырехполюсника

Комплексные функции четырехполюсника представляют отно­шения между напряжениями и токами на его зажимах и явля­ются его важными вторичными Параметрами. Они характеризуют

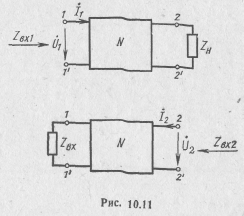
четырехполюсник в любом режиме работы, не накладывая ограничений на параметры внешних цепей.

К входным комплексным функциям четырехполюсника (рис. 10.11) относятся:

входная проводимость и обратная ей величина — входное со­противление:

выходная проводимость и обратная ей величина — выходное сопротивление:

(10.27)

Обращаясь к уравнениям четырехполюсника (10.8), заметим, что

; (10.28)

, т. e. . (10.29)

Выразив U₂ из уравнения (10.29) и подставив его в выраже­ние (10.28), найдем

или (10.29)

Аналогично (предполагая E_BX = 0) получим

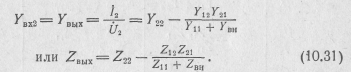
К числу комплексных передаточных функций четырехполюс­ника относятся:

передаточные функции или коэффициенты передачи по напря­жению и по току:

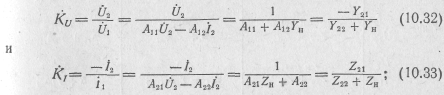
рабочий коэффициент передачи по напряжению, учитывающий как сопротивление нагрузки, так и внутреннее сопротивление источника.

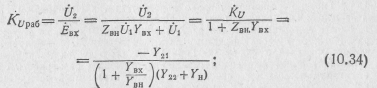
Передаточная проводимость и передаточное сопротивление:

и (10.35)

В табл. 10.3 сведены формулы, необходимые для расчета ком­плексных функций четырехполюсника через его Y- и Z-параметры, а также через определители матрицы его контурных сопротивле­ний (МКС) и определители матрицы его узловых проводимостей (МУП). Они получены с учетом формул (10.9), (10.13), (10.15) и (10.16).

Пример 10.3.

Найти комплексные функции гиратора¹ (рис. 10.12), нагруженного на coпротивление Z_H.

¹ Гиратор — элемент, широко используемый в современном анализе и син тезе цепей. Он применяется в микроволновых и твердотельных системах и мо жет быть практически создан на электронных схемах или за счет использования различных физических эффектов, таких, как эффект Холла в полупроводниках или эффект Фарадея в ферритах. Гирагор характеризуется направлением гирации (стрелкой) и коэффициентом гирации R, имеющим размерность сопротивления. Гиратором называется линейный пассивный невзаимный четырехполюсник, для которого Z₁₁=Z₂₂=0, a Z₂₁= —Z₁₂=R.

Решение.

1. Входное сопротивление нагруженного гиратора

(10.36)

обратно пропорционально сопротивлению нагрузки. Гиратор преобразует сопро­тивление нагрузки как по значению, так и по характеру.

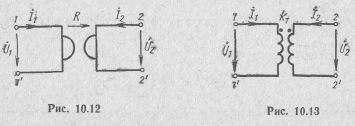
Если на выходе гиратора подключить емкость С_Н, то на его вход она транс­формируется в индуктивность, численно равную при R=1 значению этой ем­кости, и наоборот. Действительно, при Z_H = 1 /jωC_H

т. e. .

Это используется для создания индуктивностей . без индуктивных катушек, что особенно важно при разработке устройств, масса и габариты которых имеют решающее значение, например интегральных схем, в которых применение ин­дуктивных катушек крайне затруднительно.

2. Комплексные передаточные функции гиратора:

(10.37)

Ток на входе гиратора пропорционален напряжению на выходе и не зави­сит ох напряжения на входе, а ток на выходе, наоборот, пропорционален на­пряжению на входе и не зависит от напряжения на его выходе:

Пример 10.4.

Найти комплексные функции идеального трансформатора¹ (рис. 10.13), на-груженного на сопротивление Z_H. Решение. 1. Входное сопротивление нагруженного трансформатора

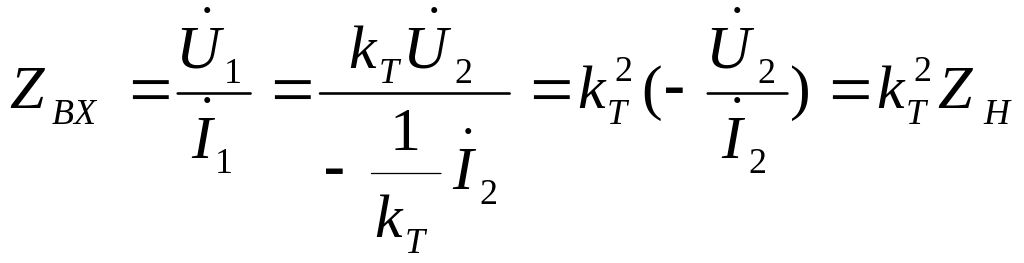(10.38)

¹ Уравнение идеального трансформатора в матричной форме:

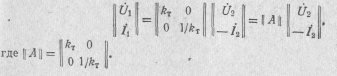
прямо пропорционально сопротивлению нагрузки. Трансформатор преобразует лишь значение сопротивления нагрузки.

2. Комплексные передаточные функции трансформатора:

(10.39)

Напряжение и ток на его выходе прямо пропорциональны соответственно напряжению и току на входе.

Пример 10.5.

Найти входное сопротивление конвертора отрицательного иммитанса (КОИ)¹, нагруженного на сопротивление Z_Н. Решение. Входное сопротивление КОИ

равно значению сопротивления нагрузки, взятому с обратным знаком. КОИ меняет знак (т. е. характер) сопротивления нагрузки. Он также позволяет создать цени с любой реактивностью без использования индуктивных катушек. Так, при Z_H=jωL_H получим