10.2. Уравнения, параметры и схемы замещения четырехполюсника

Пусть к зажимам 1—1´ четырехполюсника, содержащего как пассивные, так и активные элементы, подключен источник э. д. с, с внутренним сопротивлением Z_BH, а к выходным зажимам

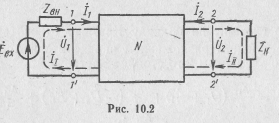
2—2' — нагрузка Z_H (см. рис. 10.2). Найдем соотношения напря­жений Ù_l, Ù₂ и токов и . Для этого запишем для рассматри­ваемой схемы систему уравнений по методу контурных токов:

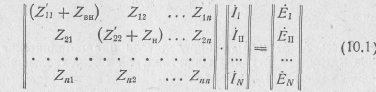
Здесь Z_jk —контурные сопротивления; и — контурные токи и э.д.с.; N = n — число независи­мых контуров в схеме. Заметим, что

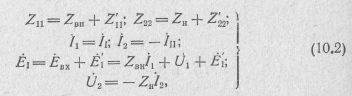
где Z´₁₁—сумма сопротивлений элементов той части I контура,

которая входит в состав четырехполюсника, но не

включает внутреннее сопротивление Z_BH источника

входного сигнала;

Z´₂₂—сумма сопротивлений элементов II контура без учета

сопротивления нагрузки Z_H.

Учитывая формулы (10.2), систему контурных уравнений (10.1) можно переписать, исключив из нее параметры источника сигнала и нагрузки:

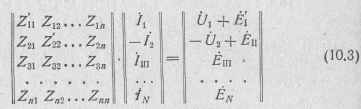
Решение системы по правилу Крамера относительно токов и с последующим разложением определителя Δ₁ по элементам 1-го, а по элементам 2-го столбца дает:

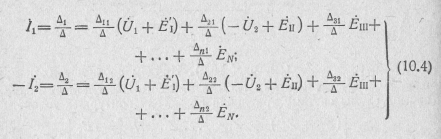
Здесь Δ, Δ₂ и Δ_jk — определители и алгебраические дополне­ния матрицы контурных сопротивлений четырехполюсника, составленной без учета внешних цепей.

Сделав следующие обозначения:

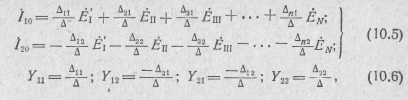
уравнения четырехполюсника (10.4) можно записать в матричной форме:

Заметим, что определители Δ и Δ_jk в формулах (10.6), а следо­вательно, и все Y-коэффициенты в выражении (10.7) являются функцией лишь схемы четырехполюсника и не зависят от пара­метров внешних цепей и действующих напряжений и токов. По­этому коэффициенты (10.6) называются параметрами четырехпо­люсника. Системе уравнений, в которой в качестве независимых переменных выбраны напряжения и , соответствуют его Y-параметры.

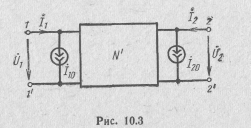
В полученных уравнениях присутствуют токи Ì₁₀ и Ì₂₀, значения которых определяются контурными э. д. с., т. е. независимыми источниками энергии, имеющимися в четырехполюснике. Эти токи равны нулю, если такие источники отсутствуют. Появление состав­ляющих (10.5) в уравнениях характерно для всех автономных активных четырехполюсников. ' Расчет таких четырехполюсников отличается лишь необходимостью учета дополнительных состав­ляющих Ì₁₀ и Ì₂₀, как это показано, например, на схеме рис. 10.3.

На ней через N' обозначен четырехполюсник, не содержащий независимых источников энергии, действие которых заменено источниками тока /ю и /₂₀.

Ниже ограничимся лишь рассмотрением четырехполюсников, не содержащих независимых источников э. д. с. и тока. В этих слу­чаях Ì₁₀ = Ì₂₀=0 и уравнения четырехполюсника упрощаются:

Здесь и в выражении (10.7)

матрица У-параметров четырехполюсника, элементы которой опре­деляются равенством (10.6). Эти параметры называют также па­раметрами короткого замыкания, так как они могут быть найдены

из опыта короткого замыкания на одной из сторон четырехполюс­ника:

в чем легко убедиться с помощью уравнений (10.8),

Пример 10.1.

Рассчитать Y-параметры четырехполюсников (рис. 10.4).

Решение.

Для схемы рис. 10.4, а с использованием матрицы контурных сопротивлений:

1. Выбрав независимые контуры (на схеме показаны пунктиром) таким образом, чтобы первый и второй контуры замыкались соответственно через за­жимы 1—1' и 2—2' четырехполюсника, составляем матрицу контурных сопро­тивлений (МКС) и находим нужные определители:

2. Y-параметры рассчитываем с помощью выражений (10.6):

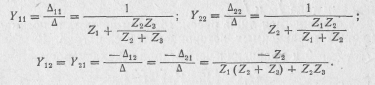
Для схемы рис, 10.4,6 с помощью опытов короткого замыкания:

I. Замыкая накоротко зажимы 2—2', с помощью уравнений (10.10) находим

2. Аналогично, замкнув зажимы 1—1', получим

Как известно, для цепей, удовлетворяющих принципу взаим­ности, Δ_jk=Δ_kj. Поэтому для всех взаимных четырехполюсников yiz — ýzi и для их описания достаточно трех параметров. Если же дополнительно к этому Y₁₂=Y₂₁, то четырехполюсник называется электрически симметричным. Для его описания достаточно лишь двух параметров. Электрическая симметрия может не соответство­вать геометрической или топологической симметрии, но последняя обязательно приводит к первой.

Если в качестве независимых переменных выбрать токи и , то полученным уравнениям соответствуют Z-параметры. Их можно найти, решив уравнения (10.8) относительно напряжений:

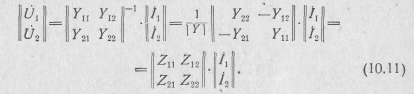
Здесь — определитель матрицы Y-пapaметров.

Таким образом,

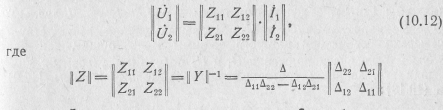
матрица Z-параметров четырехполюсника. Она обратна матрице Y-параметров.

Преобразовав выражение в знаменателе по известной формуле

где Δ_jj,kk — двойное алгебраическое дополнение, получаемое из определителя Δ, и вычеркнув две строки и два столбца с номе­рами j и k, получим

Значения Z-параметров, так же как и Y-параметров, являются функцией лишь схемы четырехполюсника. Эти параметры известны под названием параметров холостого хода, так как они могут быть определены из опыта холостого хода на одной из сторон четырех­полюсника:

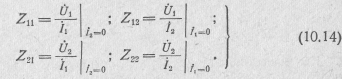
Для взаимных четырехполюсников Z₁₂ = Z₂₁.

С истемы Y- и Z-параметров дуальны. Совместно они образуют группу иммитансных (Immittance) параметров. Смысл каждого из них легко выяснить из фор­мул (10.10) и (10.14). Например, Y₁₁ и Y₂₂ — комплексные входные проводи­мости четырехполюсника относительно зажимов 1—1´ и 2—2' соответственно в режиме короткого замыкания на про­тивоположной стороне, а Y₂₁ и Y₁₂— комплексные передаточные проводимости .в этих режимах. Выражения (10.9) и (10.13) для Y- и Z-параметров найдены из контурных уравнений (10.3) и представляют отношения алгебраи­ческих дополнений и определителя матрицы контурных сопротив­лений. Используя принцип дуальности, получим аналогичные фор­мулы на основе метода узловых напряжений, который дуален методу контурных токов. При этом учтем, что в схеме (см. рис. 10.2) I и II контурам дуальны 1-й и 2-й независимые узлы (зажимы 1 и 2), а контурным токам = и = - дуальны узловые напряжения и . Дуальный случай соответствует четырехполюснику, у которого зажимы 1´-2' общие, так как только тогда оба напряжения и могут быть узловыми. Учи­тывая это, запишем соотношения, дуальные выражениям (10.9) и (10.13):

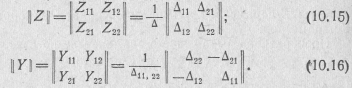
Здесь в отличие от выражений (10.9) и (10.13) алгебраические дополнения и определитель относятся уже к матрице узловых проводимостей четырехполюсника.

Пример 10.2.

Рассчитать Y-параметры четырехполюсника (рис. 10.5).

Решение.

1. Выбрав в качестве независимых 1, 2 и 3-й узлы, составляем матрицу узловых проводимостей схемы и находим нужные определители:

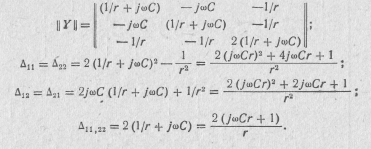
2. Y-параметры четырехполюсника рассчитываем с помощью формулы (10.16);

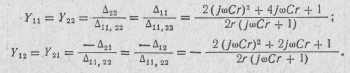
Выбирая в качестве независимых переменных напряжение и ток на выходе или входе четырехполюсника ( ,- или , ), исходя из выражений (10.8), получим еще две системы уравнений:

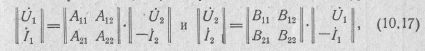
где

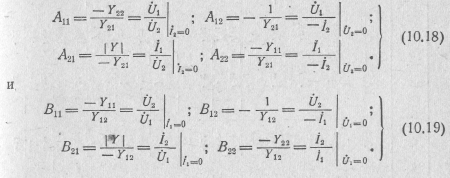
Коэффициенты А и B в этих уравнениях по смыслу представ­ляют комплексные передаточные функции четырехполюсника по напряжению и току в режиме холостого хода или короткого замыкания и называются его параметрами передачи,

Для взаимных четырехполюсников Y₁₂=Y₂₁ и

(10.20)

Если же напряжение и ток выразить через и или наоборот, то соответственно получим:

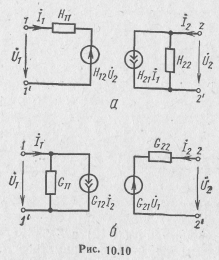
Коэффициенты Н и G в этих уравнениях по смыслу являются комплексными входными и передаточными функциями четырех­полюсника в соответствующих режимах и составляют группу гиб­ридных или смешанных параметров.

Системы H- и G-параметров дуальны. Для взаимных четырех­полюсников, так как Y₂₁ = Y₁₂,

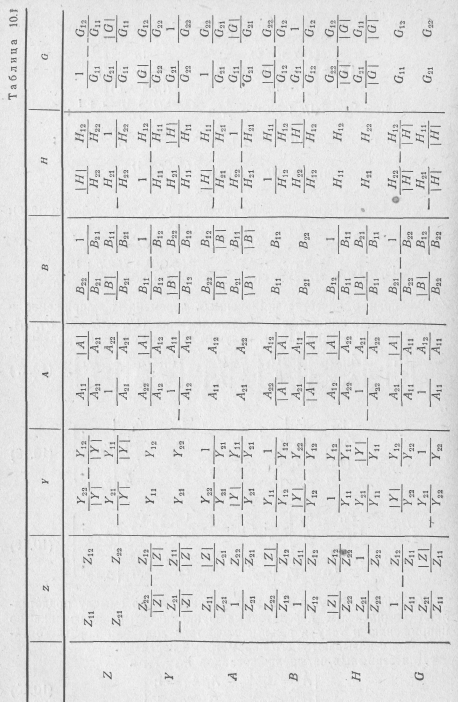
Системы параметров в формулах (10.11), (10.18) и (10.19) вы­ражены через Y-параметры. Аналогично можно выразить каждую систему параметров четырехполюсника через любую другую, полу­чив при этом формулы пересчета (табл. 10.1). Соотношения для взаимных и для симметричных четырехполюсников сведены в табл. 10.2.

Кроме полученных шести систем параметров часто используют еще одну — систему односторонних параметров, т. е. измеренных на одной из сторон четырехполюсника. Она представляет комбина­цию иммитансных параметров:

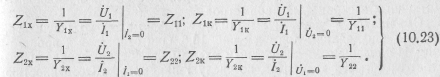
Все измерения, нужные для определения этих параметров, про­изводятся на одной из сторон четырехполюсника. Это особенно удобно, когда геометрические размеры цепи велики, например в линии связи. Первый индекс в принятых обозначениях указывает сторону, на которой производятся измерения, а второй — режим другой стороны: холостой ход или короткое замыкание.

Для симметричных четырехполюсников

(10.24)

Из четырех параметров, приведенных в формулах (10.23), лишь три являются независимыми, так как существует соотношение, связывающее их между собой:

(10.25)

Оно вытекает из равенства , которое следует из формул табл. 10.1. Поэтому односторонних параметров достаточно лишь для описания взаимных четырехполюсников.

Таким образом, линейные соотношения между напряжениями и токами на зажимах четырехполюсника характеризуются шестью разными способами с помощью Υ- и Z-, А- и В-, Н- и G-параметров. Эти параметры называются обычными или общепринятыми. При решении конкретных задач оказывается удобной и приме­няется та или иная система параметров или их комбинация. Па-пример, при расчете транзисторных схем широко применяются Υ-и H-параметры. Для многих четырехполюсников существуют не все виды обычных параметров или даже их вообще не существует. Значения рассмотренных параметров четырехполюсника опреде­ляются лишь его схемой, но зависят от выбора тех или иных вели­чин в качестве независимых переменных, что и определяет разли­чия между системами этих параметров. Поэтому они относятся к числу первичных параметров четырехполюсника. По смыслу все общепринятые параметры четырехполюсника представляют его комплексные входные или передаточные функции в режимах ко­роткого замыкания или холостого хода, т. е. без учета цепей, к которым он подключается.

Каждой из систем уравнений четырехполюсника можно приве­сти в соответствие эквивалентные схемы, схемы замещения или модели четырехполюсника, соотношения напряжений и токов на зажимах которых описываются данной системой уравнений. Наи­большее применение получили эквивалентные схемы на базе иммитансных и гибридных параметров.

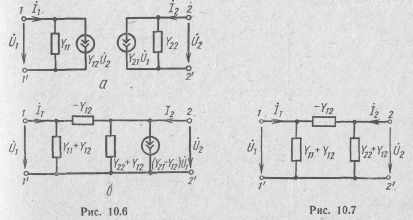
Обращаясь к уравнениям (10.8) в Y-форме, легко убедиться, что они справедливы для схем рис. 10.6. Они относятся к простей­шим П-образным эквивалентным схемам четырехполюсника и со­стоят из четырех элементов, по числу Y-параметров. Особенностью

приведенных схем является наличие зависимых, неавтономных источников энергии. Для взаимных четырехполюсников (Y₁₂= Y₂₁) эквивалентная схема упрощается, становясь трехэлементной (рис. 10.7).

Обращаясь к уравнениям (10.12) в Z-форме, можно построить эквивалентные схемы на базе Z-параметров (рис. 10.8). Они дуальны схемам рис. 10.6. Для взаимных четырехполюсников

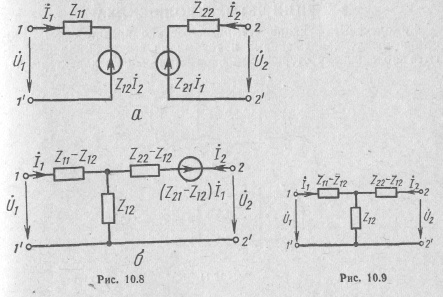
(Z₁₂=Z₂₁) получим трехэлементную Т-образную схему замещения (рис. 10.9). Аналогично можно получить эквивалентные схемы на базе H- и G-параметров (рис. 10.10).

Все схемы замещения эквивалентны одна другой и являются лишь разными формами эквивалентного представления данного четырехполюсника. При замене Четырехполюсника эквивалентной схемой распределение напряжений и токов во внешней цепи остается неизменным.