9.5. Полоса пропускания и коэффициент прямоугольности

Полосой пропускания системы связанных колебательных кон­туров называется интервал частот, в пределах которого_значение тока во втором контуре не снижается ниже уровня своего максимального значения. Ширина полосы пропускания зависит от глубины связи: чем больше фактор связи A, тем шире полоса пропускания (см. рис. 9.10). Ширину полосы пропускания системы можно регулировать изменением связи. Однако это возможно в ограниченных пределах. Наиболее широкой полоса пропускания будет, когда впадина резонансной кривой достигнет уровня , т. е. когда

Этому соответствует значение . При А>2,41 полоса пропускания системы разрывается на части, так как впа­дина резонансной кривой опускается ниже указанного уровня. Установим пределы, в которых может находиться полоса пропу­скания системы двух связанных идентичных колебательных кон­туров.

При А<1 максимальное значение вторичного тока . С учетом выражения (9.63) значения расстроек ξ_ГР, соответствую­щие границам полосы пропускания, найдем из равенства

Это равенство приводит к биквадратному уравнению , решением которого является

Здесь знак «минус» под радикалом приводит к мнимым значе­ниям , лишенным физического смысла, и не должен учиты-

ваться. С помощью выражения (9.60) находим, что значениям ξ_гр соответствуют граничные частоты

и полоса пропускания

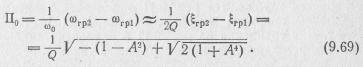
При очень слабой связи ( ), когда ,

(9.70)

При А>1 максимальное значение вторичного тока и граничные значения обобщенных расстроек ξ_гр можно найти из равенства

Ему соответствует уравнение , из которого следует

. (9.72)

Здесь знак «минус» под радикалом соответствует границам раз­рыва полосы пропускания при A = 2,41.

Отсюда аналогично выражению (9.69) находим

Максимальное значение полосы пропускания системы, соответ­ствующее А = 2,41, составляет

. (9.74)

Таким образом, в зависимости от значения фактора связи А полоса пропускания системы связанных контуров может изме­няться по ширине в пределах от 0,64 до 3,1 полосы пропускания одиночного колебательного контура. Это ценное свойство системы связанных контуров широко используется на практике. Еще более расширить полосу пропускания системы можно путем искусствен­ного уменьшения добротности контуров Q, внося в них дополни­тельные потери, например шунтирования одного из контуров активным сопротивлением.

Аналогично рассчитывается полоса пропускания системы на уровне 0,1 и коэффициент прямоугольности , ха-

растеризующий ее избирательность. В результате получим: при очень слабой связи ; при критиче­ской связи (A=1) ; при максимально допусти­мой связи (A = 2,41) . Полученные результаты указывают, что избирательность системы двух связанных конту­ров гораздо выше, чем одиночных колебательных контуров.

6. Понятие о многосвязанных колебательных контурах

Многосвязанными называют системы из трех и более связан­ных колебательных контуров. С их помощью удается еще более повысить избирательность резонансной системы. Избирательность

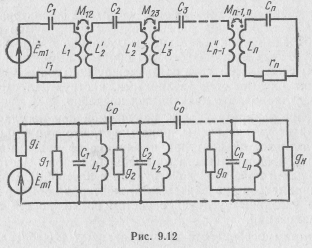
тем выше, чем больше число связанных контуров в системе. Наи­более распространенными видами связи являются индуктивная и емкостная (рис. 9.12).

Резонансные явления в многосвязанных контурах усложняются с увеличением числа связанных контуров. Число независимых пе­ременных, позволяющих описать систему, определяет число ее степеней свободы и количество резонансных частот. Расчет коле­бательных систем с многими степенями свободы с принципиальной стороны несложен. Однако с ростом числа степеней свободы вы­кладки становятся очень громоздкими, и для сложных систем их практически удается провести только с помощью электронных вы­числительных машин.

Частотные характеристики системы связанных контуров имеют несколько максимумов по числу резонансных частот. В общем

случае эти максимумы различаются по величине, что приводит к неравномерности частотных характеристик в полосе пропускания и снижению избирательности системы. Исследование частотно-избирательных свойств многосвязанных контуров показывает, что наибольшая избирательность в них достигается, если потери во всех промежуточных контурах отсутствуют.

Контуры без потерь, из которых должна состоять высокоизби­рательная система, практически осуществить нельзя. Тем не ме­нее, если промежуточные контуры имеют достаточно высокую доб­ротность, влияние потерь на избирательность системы сильно сни­жается. Этим влиянием можно практически пренебречь, если от­носительная полоса пропускания системы и добротность проме­жуточных контуров связаны соотношением

Однако повышение добротности промежуточных контуров еще не обеспечивает полного выравнивания частотных характеристик и связанную с этим возможность получить наибольшую избира­тельность системы.

Чтобы добиться равномерности частотных характеристик, τ. е. чтобы обеспечить на них равенство всех максимумов и миниму­мов, необходимо дополнительно к условию отсутствия потерь в промежуточных контурах особым образом выбрать и остальные параметры схемы. При этом связь между контурами или реактив­ности в них оказываются различными, а структура схемы стано­вится нерегулярной, что практически неудобно.

Сравнение избирательности, получаемой при регулярной и не­регулярной структуре схемы, показывает, что при выборе одина­ковых реактивностей контуров и одинаковой связи между ними проигрыш в избирательности не очень большой. Часто он оку­пается большей простотой конструкции и настройки всей системы. Выбор параметров колебательных контуров обычно делается исходя из указанных условий с учетом возможностей их практи­ческой реализации.

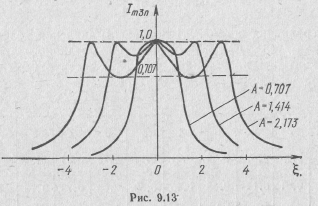
Рассмотрим особенности многосвязанных колебательных кон­туров на примере системы из трех связанных контуров регуляр­ной структуры. Анализ ее частотных характеристик показывает, что на них число экстремумов зависит от фактора связи A. При имеется лишь один экстремум, которому соответ­ствует резонанс в системе и одногорбая резонансная кривая. При резонансная кривая становится трехгорбой (рис. 9.13). Ординаты всех горбов и впадин одинаковы. С увеличением фак­тора связи глубина впадин растет, а горбы раздвигаются. При A>2,173 полоса пропускания имеет разрывы. Значение A = 2,173 определяет максимально допустимую связь, которой соответствует наибольшая полоса пропускания

(9.75)

и коэффициент прямоугольности

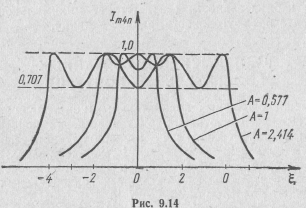
Для сравнения на рис. 9.14 показаны резонансные характери­стики системы четырех связанных контуров регулярной струк­туры при отсутствии потерь в промежуточных контурах, При

кривые трехгорбые, а при A>1—четырехгорбые. Максимально допустимая связь в этом случае определяется зна­чением ,

Существенной особенностью системы связанных контуров в отличие от одиночного колебательного контура является не только более высокая избирательность, но и ее зависимость от парамет­ров схемы. Наиболее высокая избирательность получается при максимальном факторе связи. С уменьшением А полоса пропуска­ния сужается, а коэффициент прямоугольности уменьшается. Во

всех случаях рост числа связанных контуров в системе приводит к улучшению ее избирательных свойств.

Для количественной оценки частотной избирательности высо­коизбирательных систем, которыми являются многосвязанные колебательные контуры, более удобным является коэффициент прямоугольное™, рассчитанный как отношение полосы пропуска­ния на уровне 0,707 к полосе пропускания на уровне 0,01:

Для сравнения в табл. 9.1 приведены значения коэффициентов прямоугольности и для различного числа n свя­занных контуров в системе с регулярной структурой и отсутст­вием потерь в промежуточных контурах.

Таблица 9.1

Часто для оценки частотной избирательности резонансных си­стем пользуются понятием коэффициента прямоугольности, взя­того как величина, обратная коэффициенту (9.76). При этом мак­симальной избирательности соответствует минимальное значение коэффициента прямоугольности, равное единице.