9.4. Частотные характеристики системы связанных колебательных контуров

Обычно при изучении частотно-избирательных свойств си­стемы связанных колебательных контуров, когда вторичный ток является выходной и э. д. с. — входной величиной (см. рис. 9.1, а), используют Т-образную схему замещения (см. рис. 9.3, а), а свойства системы характеризуют передаточной про­водимостью . Если же выходной величиной служит напряже­ние на вторичном контуре, а входной — ток источника (см. рис. 9.2), то пользуются П-образной схемой замещения (см. рис. 9.3,6), а систему характеризуют передаточным сопротивле­нием .

Передаточную проводимость обобщенной Т-схемы находим из выражения (9.22), учитывая формулы (9.6), (9.7), (9.11), (9.36) и (9.43):

(9.47)

При полном резонансе ( ) она имеет значение

(9.48)

Нормируя по этой величине передаточную проводимость си­стемы, получаем

Модуль этой функции представляет нормированную обобщен­ную АЧХ системы связанных контуров, совпадающую с ее норми­рованной резонансной характеристикой:

В случае идентичных контуров |₁ = ^2 ⁼ | и

Передаточное сопротивление обобщенной П-схемы находим из формулы (9.23):

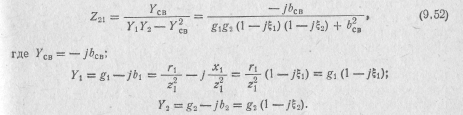
При основном резонансе, когда , функция (9.52) имеет максимум, если

, т. е. при

. (9.53)

Подставляя выражение (9.53) в формулу (9.52), при , получаем значение передаточного сопротивления при резонансе

(9.54)

Нормируя по этой' величине передаточное сопротивление системы, находим

, (9.55)

где

(9.56)

фактор связи.

Модуль этой функции представляет нормированную обобщенную A4X (ре­зонансную характеристику) системы и, как следует из формулы (9.50), совпа­дает с нормированной резонансной характеристикой Т-схеми:

Формулы (9.49) и (9.55) являются наиболее общим выраже­нием частотных характеристик системы связанных колебательных контуров. С их помощью характеристики системы выражаются че­рез обобщенные расстройки и , ко­торые в свою очередь могут быть определены как через частоту ω при заданных первичных параметрах контуров, так и через пер­вичные параметры контуров при заданной частоте ω. Эти формулы позволяют анализировать как резонансные, так и настроечные кри­вые системы независимо от того, состоит она из одинаковых или из разных контуров, настроенных одинаково или по-разному.

Нормированные обобщенные АЧХ, определяемые формулами (9.50) и (9.57), при каждом значении постоянной Л представ­ляют поверхность второго порядка в системе координат или , и . Эти функции стремятся к нулю как при , так и при . Плоскость с координатами и называется пло­скостью расстроек. При изменении фактора связи А обобщенные АЧХ образуют над плоскостью расстроек семейство поверхностей, характер которых зависит от значения А.

Для изучения этих поверхностей пользуются методом сечений. Его суть в том, что исследование поверхности производится путем изучения кривых, образованных при пересечении поверхности пло­скостями, нормальными или параллельными плоскости расстроек.

При первом способе, рассекая поверхность I_m2n = f( ; ; A) плоскостью, нормальной плоскости расстроек, получаем каждый раз след сечения, характер которого зависит от положения секу­щей плоскости (рис. 9.7). Положение секущей плоскости пол­ностью определяется взаимосвязью расстроек и , τ. е. зависит от соотношения параметров контуров.

При заданной частоте сигнала ω изменения \\ и ..₂ определя­ются изменением параметров контуров. Тогда, например, случай =var, = const (рис. 9.7, а) соответствует настройке на первый частный резонанс, а случай = const; = var (рис. 9.7, б) — на­стройке на второй частный резонанс. Следы сечений при этом являются настроечными кривыми.

При неизменных параметрах колебательных контуров измене­ния и определяются изменением частоты ω. Тогда след сечения, получающийся, например, в случае (рис.9.7,б), представляет резонансную кривую системы идентичных связанных контуров, а следы сечений в случаях , когда = var, =var (рис. 9.7,г), — резонансные кривые системы неидентичных кон­туров.

При втором способе исследования поверхности обобщенной АЧХ она рассекается на определенных уровнях, например при I_m2n = 0,l; 0,2; ...; 0,9, плоскостями, параллельными плоскости расстроек. Фиксация получаемых следов сечений приводит к топо­графическим диаграммам (рис. 9.8, 9.9). Каждой поверхности с определенным значением А соответствует своя топографическая диаграмма. С помощью таких диаграмм можно построить резо-

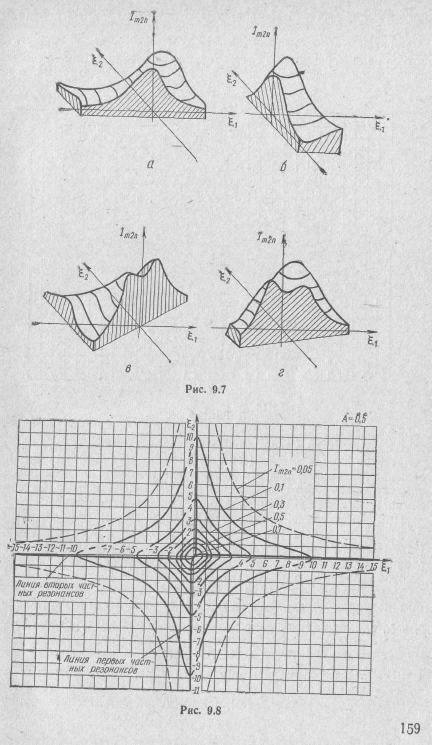
нансные и настроечные кривые для данной системы связанных, контуров.

Участки топографической диаграммы, на которых линии рав­ного уровня сгущаются, соответствуют более крутым участкам исследуемой поверхности, и наоборот. Точки на диаграмме, в ко-

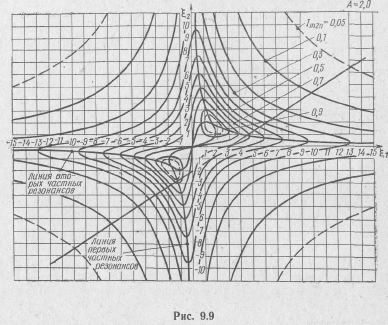
торых достигается максимальное значение аппликаты 1_т2n при пе­ремещении вдоль оси ( = var; = const), соединены линией, называемой линией первого частного резонанса. Аналогичная ли­ния, но соответствующая перемещению вдоль оси ( =const; =var), называется линией второго частного резонанса.

При любых изменениях расстройки и максимум вторич­ного тока соответствует точкам на линиях частных резонансов. Наибольшее значение этого максимума указывает точки сложного резонанса. Частоты, соответствующие точкам на этих линиях, яв­ляются резонансными частотами системы.

Резонансные и настроечные характеристики системы связан­ных контуров по своей форме и виду зависят от соотношения и , т. е. от соотношения параметров обоих контуров и , и

Для простоты анализа обратимся к системе идентичных кон­туров (Q₁= Q₂ = Q; ω₁=ω₂=ω₀), частотные характеристики кото­рых описываются выражением (9.51). Эта функция

при каждом значении А представляет кривую в плоскости коор­динат и ξ. Исследуем ее на экстремум:

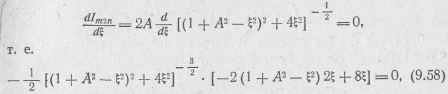
откуда

.

Корни полученного уравнения представляют три значения обобщенной расстройки, соответствующие точкам экстремума:

. (9.59)

Этим значениям соответствуют частоты, которые можно выра­зить через и с помощью формулы (7.27):

, т.е. . (9.60)

В результате получаем частоты экстремумов:

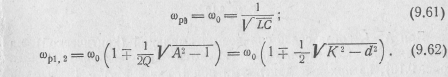
Частота ω_р0 соответствует собственной резонансной частоте кон­туров ω₀. Частоты ω_р1,2 сдвинуты в обе стороны от ω₀ на вели­чину называются частотами связи. С уменьшением связи частоты связи сближаются, и при А=1 совпадают с частотой ω₀. Анализ полученных выражений показы­вает, что число экстремумов на резонансной кривой зависит от значения фактора связи А.

При А<1, когда связь между контурами слабее оптимальной, имеется лишь один экстремум при , так как и — в этом случае мнимые величины и не имеют физического смысла. Этому экстремуму соответствует резонанс в системе на частоте . Вторичный ток в формуле (9.51) при резонансе не достигает своего максимально возможного значения (рис. 9.10), так как

(9.63)

В случае A<1 в системе достигаются лишь частные резонансы.

При А = 1, когда связь оптимальная, имеется также лишь один экстремум при . Ему соответствует резонанс на ча­стоте . В отличие от предыдущего случая вторичный ток

при оптимальной связи достигает своего максимально возможного значения:

В случае A = 1 в системе достигается полный резонанс. Связь с A = 1 называется также критической связью.

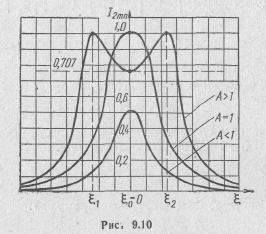
При А>1, когда связь сильнее оптимальной (критической), на резонансных характеристиках имеются три экстремума (см. рис. 9.10), из них два максимума при и один

минимум или впадина при =0. Максимальным значениям вто­ричного тока соответствуют две точки резонанса на частотах связи . Вторичный ток в этих точках достигает своего макси­мально возможного значения:

Этому соответствует настройка системы на первый или второй сложный резонанс.

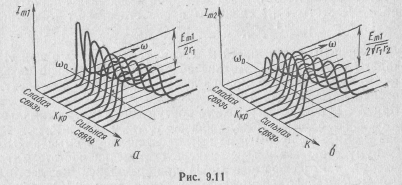
При резонансные кривые — одногорбые, а при A>1 — двугорбые. С увеличением фактора связи A точки максимумов (точки резонанса) раздвигаются, но ординаты максимумов оста­ются неизменными. С раздвиженнем горбов впадина между ними становится глубже. На рис. 9.11,а показана зависимость формы резонансной кривой вторичного тока от коэффициента связи. Для сравнения на рис. 9.11,6 приведена аналогичная зави­симость резонансной кривой первичного тока.