т. е. значения комплексной функции цепи при сопряженных часто­тах являются сопряженными. Действительно, как следует из вы­ражения (6.5):

Исходя из этих выражений, приходим к выводу о четности ве­щественной части R(ω) и модуля K(ω) комплексной функции ли­нейной цепи, а также о нечетности ее мнимой части X(ω) и аргу­мента φ(ω):

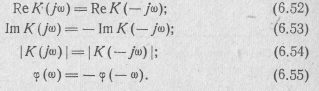
Для входных и некоторых передаточных комплексных функ­ций цепи характерно, что между их компонентами существуют определенные связи. Тогда комплексная функция может быть най­дена, если известен один из ее компонентов. Это особенно важно при решении задач синтеза. Такие функции называются функ­циями минимальной фазы, а соответствующие им цепи — мини­мально фазовыми. Связь между компонентами функций минималь­ной фазы является следствием известного из теории функций комплексного переменного положения, по которому вещественная и мнимая части функции, аналитической в правой полуплоскости комплексного переменного и на мнимой оси ƒω, связаны между собой преобразованием Гильберта.

К числу минимально фазовых относится широкий класс линей­ных цепей. При их проектировании нельзя произвольно задавать АЧХ и ФЧХ во всем диапазоне частот. Свойства комплексных функций широко используются при решении задач синтеза.

6.5. Расчет комплексных функций цепи с помощью матриц ее контурных сопротивлений и узловых проводимостей

Расчет комплексных функций цепи удобно проводить методом контурных токов или узловых напряжений. Выбор метода в каж­дом конкретном случае определяется числом уравнений в системе. Перед расчетом выделяются точки приложения входной величины и действия выходной величины (см. рис. 6.2),

Расчет методом контурных токов сводится к нахождению мат­рицы контурных сопротивлений схемы и определению с ее по­мощью требуемых функций цепи. При составлении матрицы контур­ных сопротивлений учитываются все элементы, за исключением внут­реннего сопротивления источника входного сигнала.

П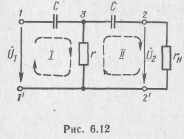 ри расчете этим методом вы­бор независимых контуров удобно сделать так, чтобы точки действия входной и выходной величин вхо­дили в состав внешних контуров (см. рис. 6.2). В этом случае рас­чет комплексных функций цепи проводится по формулам (6.16) — (6.18), сведенным в табл. 6.2.

Пример 6.1.

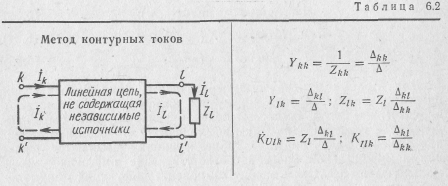
Рассчитать комплексную передаточную функцию по напряжению и соответ­ствующие ей АЧХ и ФЧХ Т-образной rC-цепи (рис. 6.12).

Решение.

1. Матрица контурных сопротивлений схемы:

2. Передаточная функция по напряжению в соответствии с формулой (6.18)

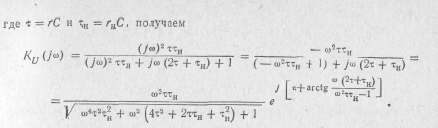
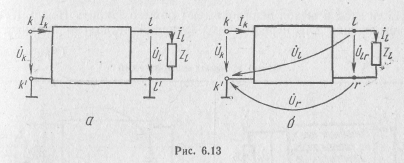
3. Амплитудно-частотная и фазо-частотная характеристики.

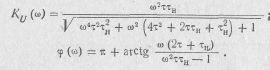
Расчет методом узловых напряжений сводится к нахождению матрицы узловых проводимостей схемы и определению с ее по­мощью требуемых функций цепи. При составлении матрицы узло­вых проводимостей учитываются все элементы схемы, за исключе­нием внутреннего сопротивления источника входного сигнала.

Если напряжения на входе и выходе цепи выбраны в качестве узловых, т. е. один из входных и один из выходных ее полюсов являются общими и выбраны в качестве базисного узла (рис. 6.13,а), то расчет функций цепи проводится по формулам (6.23)-(6.25).

Пример 6.2.

Рассчитать комплексную передаточную функцию по напряжению и соответ­ствующие ей АЧХ и ФЧХ Т-образной rC-цепи (см. рис. 6.12). Решение. 1. Матрица узловых проводимостей схемы:

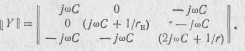
2. Передаточная функция по напряжению в соответствии с формулой (6.25):

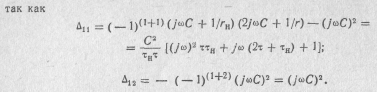
Полученный результат и дальнейший ход расчета совпадают с уже сделан­ным в примере 6.1.

Если вход и выход цепи не имеют общего зажима (рис. 6.13,6), то выражения для передаточных функций несколько изменяются

Таблица 6.3

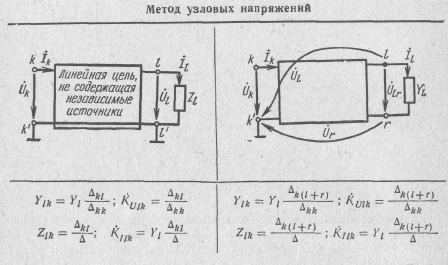
(табл. 6.3). Действительно, в отличие от выражений (6.23) — (6.25) в этом случае получим:

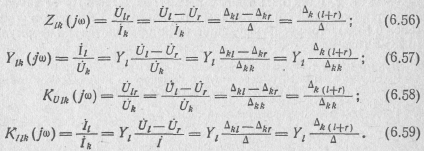
Здесь —суммарное алгебраическое дополнение мат­рицы узловых проводимостей схемы. В нем одиночный индекс k указывает на номер вычеркиваемой строки. Первый индекс l в скобках указывает на номер столбца, элементы которого пере-

носятся со следующим за этим индексом знаком « + » в столбец г, номер которого соответствует второму индексу в скобках. Знак суммарного алгебраического дополнения определяется множите­лем (—1) в степени, равной сумме одиночного индекса и первого из двух индексов, взятых в скобки: (— 1 )^(k+^l),

Пример 6.3.

Рассчитать комплексную передаточную проводимость измерительной мостовой схемы (рис. 6.14).

Решение. _

1. Матрица узловых проводимостей схемы:

2. Передаточная проводимость в соответствии с выражением (6.57):

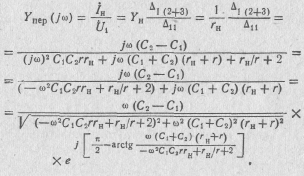
так как

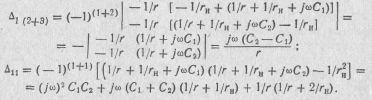
7. ПОСЛЕДОВАТЕЛЬНЫЙ

КОЛЕБАТЕЛЬНЫЙ КОНТУР

7.1. УСЛОВИЕ РЕЗОНАНСА И ОСНОВНЫЕ

ПАРАМЕТРЫ КОНТУРА

П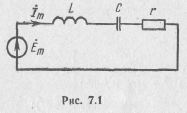 оследовательным колебательным контуром называют цепь, состоящую из последовательного соединения индуктивности L и емкости С .(рис. 7.1). Потери в элементах контура учитываются

сопротивлением г. В таком контуре может возникать резонанс напря­жений, т. е. явление, при котором на реактивных элементах контура появляются напряжения, значи­тельно превышающие напряжения, действующие на входе контура. Это является следствием того, что при резонансе реактивное сопротивле­ние последовательного контура оказывается равным нулю:

. (7.1)

Это равенство и является условием резонанса напряжений. Ре­зонансом называется явление, при котором сопротивление контура становится чисто активным. При этом ток в контуре достигает своего максимального значения, чем и объясняется возрастание напряжений на его элементах. Частота, при которой реактивное сопротивление контура равно нулю, т. е. выполняется условие ре­зонанса напряжении,

(7.2)

называется резонансной частотой контура. Резонансная частота последовательного контура полностью определяется параметрами его реактивных элементов.

Когда частота сигнала совпадает с частотой резонанса (ω = ω₀), говорят, что контур настроен на частоту сигнала. Если же

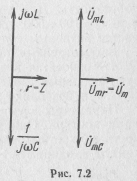, то контур расстроен. Расстройка контура тем сильнее, чем больше его реактивное сопротивление х, и равна нулю, если x = 0. При резонансе реактивные сопротивления индуктивности и емко­сти контура равны между собой:

·

Сопротивление индуктивности или емкости контура при резо­нансе называется волновым или характеристическим сопротивле­нием контура

(7.3)

Учитывая выражение (7.2), получим

(7.4)

Волновое сопротивление является одним из важных параметров контура. Оно не за­висит от частоты и определяется только параметрами его реактивных элементов. Для радиотехнических контуров харак­терны значения Ом.

Сопротивление последовательного коле­бательного контура при резонансе минимально и равно активному сопротивлению контура. Действительно, с учетом формулы (7.1), находим

. (7.5)

Поэтому ток, протекающий в контуре при резонансе, максима­лен и ограничивается лишь активным сопротивлением контура:

. (7.6)

Напряжения на реактивных элементах контура при резонансе равны по амплитуде и обратны по фазе (рис. 7.2):

; (7.7)

(7.8)

По своему значению они тем выше, чем больше волновое сопро­тивление контура ρ. Если ρ>r, то напряжения на реактивных эле­ментах при резонансе значительно превышают напряжение источ­ника.

Отношение напряжения на реактивном элементе контура (ин­дуктивности или емкости) при резонансе к напряжению, действую-

щему на входе контура, определяет эффективность или качество контура и называется его добротностью

(7.9)

Величина, обратная добротности, носит название затухания контура

(7.10)

Чем меньше активное сопротивление контура, тем выше его добротность. Для радиотехнических контуров характерны значе­ния Ом. Добротность контура практически ограничи­вается активным сопротивлением индуктивной катушки.

Рассмотренные параметры колебательного контура: ω₀, ƒ₀, T₀, ρ, Q, d — относятся к числу вторичных параметров. Они характери­зуют основные свойства контура без учета конкретных значений L, С, r и позволяют сравнить различные колебательные контуры.

Параметры элементов L, С, r являются .первичными парамет­рами контура. Они характеризуют данный контур как совокуп­ность конкретных элементов и позволяют отличить его от других контуров, например с такими же ω₀, ρ, Q.

Пример 7.1.

Найти резонансную частоту последовательного колебательного контура и напряжение на его емкости при резонансе, если напряжение входного сигнала U_m= 10 мВ, а параметры элементов; r=5 Ом; L=1 мГ; С=360 пФ.

Решение.

1. Резонансная частота контура:

2. Добротность контура:

3. Напряжение на емкости:

Физику процессов в колебательном контуре удобно рассмотреть на основе анализа энергетических соотношений. Пусть при резо­нансе в контуре протекает ток

i(t) = I_mcos ω₀t.

Тогда на емкости действует напряжение

Энергия, запасаемая в магнитном поле катушки индуктивности,

. (7.11)

Энергия, запасаемая в электрическом поле конденсатора:

Так как при резонансе .x₀ = 0, то

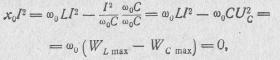
т. е.

При резонансе максимум энергии, накапливаемой в индуктив­ности, равен максимуму энергии, накапливаемой в емкости. Пол­ная энергия, накопленная в контуре при резонансе в любой момент времени, равна сумме

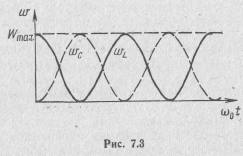
Отсюда следует вывод, что при резонансе суммарная энергия, запасенная в контуре, остается неизменной: происходит лишь не­прерывное периодическое перераспределение (колебание) энергии, запасенной в индуктивности и емкости (рис. 7.3). В момент когда энергия магнитного поля индуктивности достигает максимума, энергия электрического поля емкости равна нулю, и наоборот; происходит обмен энергией между индуктивностью и емкостью. Источник энергии входного сигнала служит для компенсации по­терь в активном сопротивлении контура. Он необходим для воз­буждения и поддержания колебаний в контуре. От источника в любой отрезок времени потребляется столько энергии, сколько ее за это время превращается в тепло в активном сопротивлении контура.

С помощью полученных энергетических соотношений можно определить качество, или добротность, контура.

где P = rI² — активная мощность, рассеиваемая в контуре;

—период колебаний при резонансе.

Добротность Q определяет отношение энергии, запасенной в контуре при резонансе, к энергии потерь в нем. Энергетическое определение добротности является наиболее общим определением для колебательного контура любого вида.