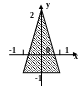Практическая работа №1 задачи на выбор

1. Прочитать и разобраться в первой части первой главы задачника («Задачи без массивов»). Решить задачу с использованием условного оператора.

1. Вводятся три целых числа. Определить, могут ли они являться сторонами треугольника.

2. Заданы два прямоугольника размерами А*В и C*D. Определить, можно ли поместить второй прямоугольник в первый при условии параллельности и перпендикулярности их сторон.

3. Вводятся два целых числа. Определить, одинаковая ли у них четность.

4. Вводятся координаты точки на плоскости (X,Y). Определить, в какой четверти находится эта точка.

5. Вводятся три целых числа. Найти из них максимальное значение.

6. Имеется стол прямоугольной формы размером а*b (а и b - целые числа, а>Ь). В каком случае на столе можно разместить большее количество картонных прямоугольников с размерами c*d (c и d- целые числа, c>d): при размещении их длинной стороной вдоль длинной стороны стола или вдоль короткой. Прямоугольники не должны лежать один на другом и не должны свисать со стола.

7. Заданы размеры плоского прямоугольного отверстия (а*b) и размеры трехмерного кирпича (c*d*e). Определить, можно ли протащить кирпич через отверстие, соблюдая параллельность и перпендикулярность сторон.

8. Вводится номер года. Определить, является ли этот год високосным (год високосный, если его номер кратен четырем, однако из кратных ста високосными являются лишь кратные четыремстам; например, 1700, 1900 - не високосные годы, а 2000 - високосный).

9. Вводятся коэффициенты (к1,b1,к2,b2), определяющие две прямые у=к1*х+b1 и y=k2*x+b2. Найти точку пересечения этих прямых или указать, что они совпадают или параллельны.

10. Даны стороны и диагонали параллелограмма. Определить, является он ромбом, прямоугольником или квадратом.

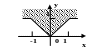
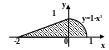
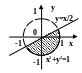
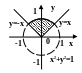
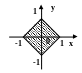
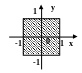
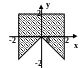
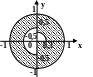
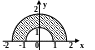
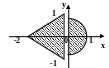
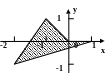
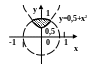
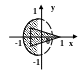
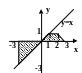
2. С клавиатуры вводится координата точки (х,у). Написать программу, которая проверяет принадлежность точки заданной области.

Номер варианта	Задание		Номер варианта	Задание
1			13
2			14
3			15
4			16
5			17
6			18
7			19
8			20
9			21
10			22
11			23
12			24

Практическая работа №2 циклы

1. Решить задачу с использованием оператора цикла.

1. Даны натуральные числа а и b (а>b). Найти результат и остаток целочисленного деления а на b, не используя стандартных операций DIV и MOD.

2. Вводится натуральное число n. Найти n-ое число Фибоначчи.

3. Вводится натуральное число n. Определить, является ли оно совершенным. Совершенным считается число, которое равно сумме своих делителей (конечно, за исключением себя самого).Например 6 - совершенное число, т.к. 6=1+2+3.

4. Вводится радиус круга R. Подсчитать, сколько точек с целочисленными координатами попадают в круг радиуса R с центром в начале координат.

5. Вводится натуральное n. Получить наименьшее число вида 2R, превосходящее n.

6. Даны натуральные числа а и b, являющиеся соответственно числителем и знаменателем дроби. Сократить дробь, найдя наибольший общий делитель (НОД(а,b)) по алгоритму Евклида. Алгоритм Евклида основан на следующем соотношении: НОД(m,n)=НОД(m mod n,n), если m и n одновременно не равны нулю и m>n, а mod - остаток от деления.

7. Вводится натуральное число n. Найти сумму первых n чисел Фибоначчи.

8. Задан прямоугольник размером А*В (А и В- натуральные). От прямоугольника каждый раз отрезаются квадраты максимальной площади. Найти общее количество квадратов.

9. Вводится факториал некоторого числа N. Найти число N.

10. Вводятся два натуральных числа. Найти их наибольший общий делитель по алгоритму Евклида d = НОД(a,b) и такие целые x и y, что d = a*x + b*y. Алгоритм Евклида основан на следующем соотношении: НОД(m,n)=НОД(m-n,n), если m и n одновременно не равны нулю и m>n.

11. Вводится число Фибоначчи. Найти его порядковый номер в последовательности n.

12. Вводится натуральное число N и цифра А. Определить, сколько таких цифр присутствует в числе N.

13. Составить программу возведения натурального числа в третью степень, учитывая следующую закономерность: 1^3=1, 2^3=3+5, 3^3=7+9+11, 4^3=13+15+17+19.

2. Вводится последовательность целых чисел, признаком окончания ввода является число 0. Определить сумму чисел, их количество, среднее арифметическое, минимальное и максимальное число с их порядковыми номерами среди тех элементов последовательности, которые обладают свойствами, указанными преподавателем:

1. находятся между 11 и 99;

2. имеют четный порядковый номер ввода;

3. кратны пяти;

4. оканчиваются на цифру нуль;

5. имеют нечетный порядковый номер ввода;

6. четные;

7. оканчиваются на цифру семь;

8. нечетные;

9. оканчиваются на цифру один;

10. оканчиваются на цифру три;

11. кратны семи;

12. кратны трем;

13. оканчиваются на цифру пять;

14. однозначные;

15. двузначные;

16. трехзначные.