2.8. Классы функций, сохраняющих 0 и 1

Определение. Говорят, что булева функция сохраняет 0, если .

Обозначим через множество функций от переменных, сохраняющих 0, а через – множество всех булевых функций, сохраняющих 0, т.е. .

Например, ; .

Определение. Говорят, что булева функция сохраняет 1, если .

Обозначим через множество функций от переменных, сохраняющих 1, а через – множество всех булевых функций, сохраняющих 1, т.е. .

Например, ; .

2.9. Класс самодвойственных функций

Определение. Говорят, что булева функция самодвойственная, если .

Обозначим через множество самодвойственных функций от переменных, а через – множество всех самодвойственных функций; т.е. .

Например, ; .

2.10. Класс монотонных функций

Определение. Если для любого ( ), то говорят, что вектор предшествует вектору и пишут .

Например, ; .

Определение. Говорят, что булева функция монотонна, если для любых наборов и значений переменных, таких что , выполняется неравенство .

Обозначим через множество монотонных функций от переменных, а через – множество всех монотонных функций; т.е. .

Например, ; .

2.11. Класс линейных функций

Определение. Говорят, что булева функция линейна, если в ее каноническом полиноме Жегалкина коэффициенты при всех слагаемых, содержащих произведения переменных, равны 0.

Обозначим через множество линейных функций от переменных, а через – множество всех линейных булевых функций, т.е. .

Например, ; .

2.12. Критерий полноты (теорема Поста)

Классы , , , , называют классами Поста.

Утверждение 1. Классы Поста неполны и попарно различны.

Чтобы убедиться в попарном различии классов Поста, составим таблицу, столбцы которой соответствуют классам , , , , , строки – функциям , а в клетках проставляется «+» или «–» в зависимости от того, принадлежит ли функция соответствующему классу или не принадлежит.

	+	–	–	+	+
	–	+	–	+	+
	–	–	+	–	+

Как видно из таблицы, для каждой пары классов найдется функция, принадлежащая одному классу из пары и не принадлежащая другому.

Теорема (Поста). Для того чтобы система функций была полна, необходимо и достаточно, чтобы множество не являлось подмножеством ни одного из классов Поста.

3.1. Начальные понятия теории графов

Определение. Пусть и - конечные множества, ; - отображение множества в множество одно и двухэлементных подмножеств множества . Тройку называют неориентированным графом (или просто графом).

Элементы множества и называют соответственно вершинами и ребрами. Множество вершин и ребер графа будем также обозначать и . Отображение называют отображением инцидентности.

П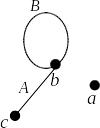 ример 1. : , , , .

Граф удобно представлять в виде диаграмм, на которых вершинам соответствуют помеченные точки плоскости, а ребрам – помеченные непрерывные кривые, соединяющие эти точки. Так, граф из примера 1 можно представить диаграммой, изображенной на рисунке.

Если , где , то говорят, что ребро соединяет вершины и . В этом случае будем писать . Если , то ребро называют петлей в вершине . В этом случае будем также писать и говорить, что соединяет вершину саму с собой.

Если - некоторое ребро данного графа, то вершины , называются смежными; говорят также, что , –концевые вершины ребра .

Ребра и называются смежными, если они имеют общую концевую вершину.

Если - концевая вершина ребра , то ребро и вершина называются инцидентными.

Если и , то ребра и называются кратными. Число ребер, инцидентных вершине , (петля учитывается дважды) называется степенью вершины и обозначается .

Если , то вершина называется изолированной.

Если , то вершина называется висячей. Ребро, инцидентное висячей вершине, называется висячим.

Пример 2. Пусть , а . Отображение инцидентности задано следующим образом: , , , , , .

Д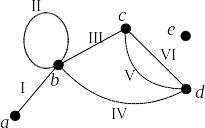 ля наглядности представим граф диаграммой.

Вершины , - концы ребра . Ребра , - кратные. Вершины и - смежные. Вершина инцидентна ребрам , , . , , , , . Вершина - висячая, ребро - висячее, вершина - изолированная.

Лемма (о рукопожатиях). Для любого графа сумма степеней вершин равна удвоенному числу ребер, т.е.

.

Следствие. В любом графе число вершин нечетной степени либо четно, либо равно 0.

Граф без петель и кратных ребер называется обыкновенным графом.

Обыкновенный граф называется полным графом, если любые его две различные вершины смежные. Для полного графа с вершинами применяется обозначение .

Пример 3.

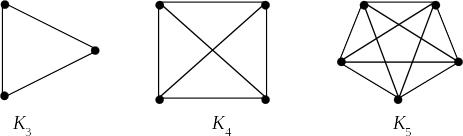
Заметим, что степень каждой вершины полного графа равна , так что

.

Следовательно, число ребер полного графа с вершинами равно .

Определение. Граф H называется подграфом графа G, если .

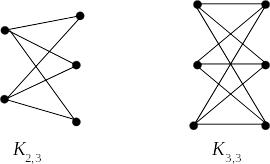
Двудольным графом называется обыкновенный граф, множество вершин которого может быть разбито на два непустых непересекающихся подмножества (доли), так что концы каждого ребра графа принадлежат разным долям.

Двудольный граф называется полным двудольным графом, если любые две его вершины, принадлежащие разным долям, смежные.

Полный двудольный граф с вершинами в одной доле и вершинами в другой ( ) обозначают .

Пример 3.