Абсолютные показатели вариации
Размах вариации R =
Показатель характеризует амплитуду колебаний признака. К его недостаткам можно отнести тот факт, что очень низкое или очень высокое значение признака может быть вызвано каким-либо случайным обстоятельством.
Среднее линейное отклонение
- простое среднее линейное отклонение
для не сгруппированных данных;
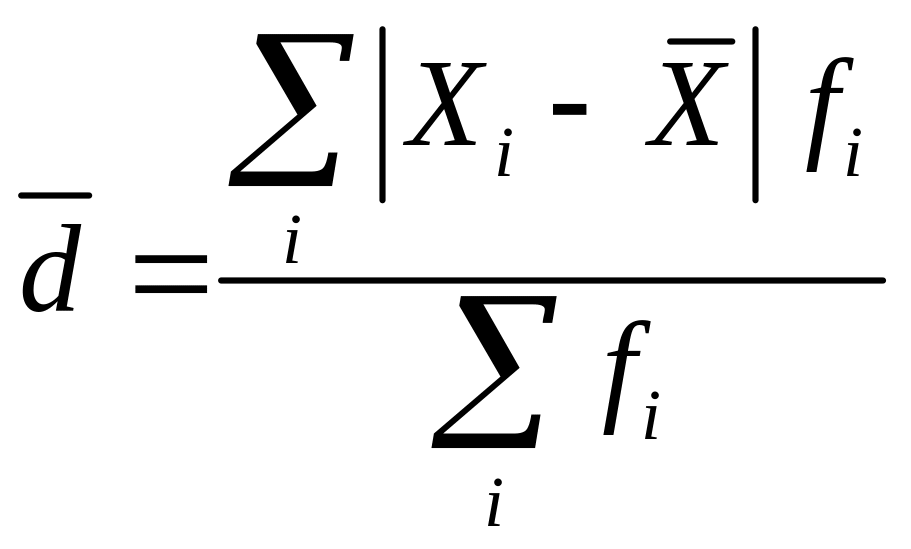- для взвешенных данных.
Дисперсия
- простая;
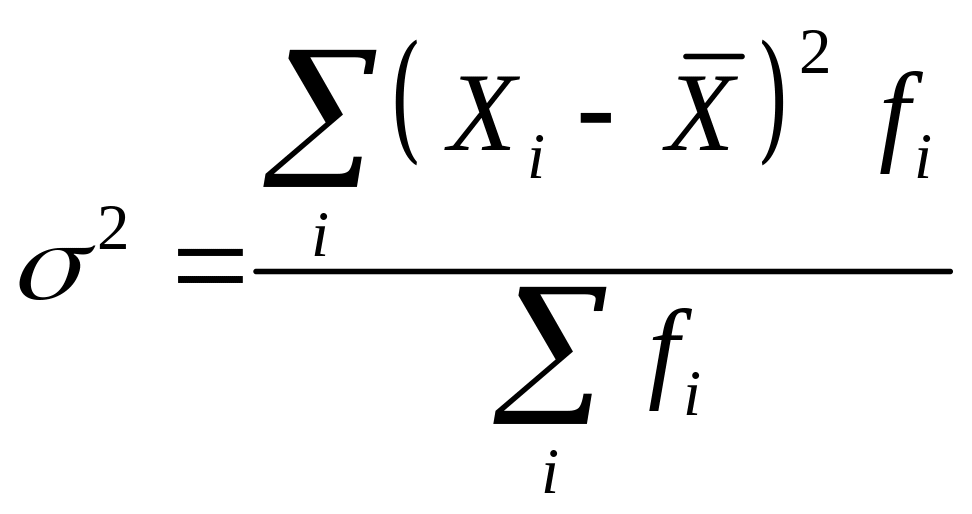- взвешенная.
Относительные показатели вариации
Дают характеристику однородности совокупности. Базой сравнения является либо среднее арифметическое, либо , в зависимости от однородности совокупности.
На практике чаще используется коэффициент вариации.
Коэффициент вариации
;
Для однородных совокупностей
.
Вариация альтернативного признака. Энтропия распределения.
В ряде случаев возникает необходимость в измерении дисперсии альтернативных признаков, т.е. признаков, которыми обладают одни единицы совокупности, а другие единицы не обладают.
Примеры таких признаков: ученая степень преподавателя вузов, работа по полученной специальности.
Значения альтернативного признака обычно задаются следующим образом:
1 – если объект обладает признаком;
0 – если не обладает.
ξ =
, p+q=1
p – доля единиц, которые обладают признаком;
q – доля единиц, которые не обладают признаком.
;
.
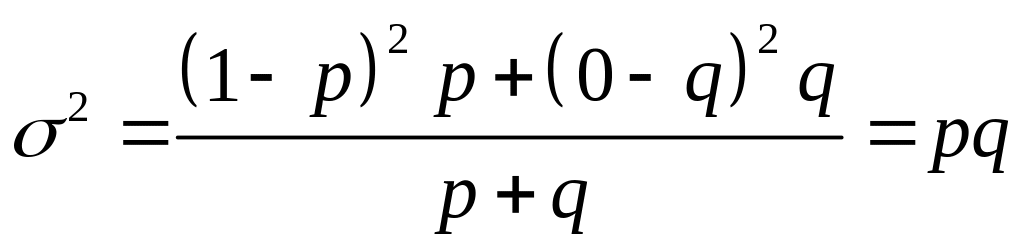p=q=0,5;
.
Энтропия – это мера неопределенности данных наблюдения. Она зависит от числа признаков и от вероятности каждого из них.
- вероятность обладать
-
ым признаком.
Если все варианты равно вероятны, т.е.
,
то энтропия максимальна.
В частности,
.
Часто в задачах рассматривают относительную энтропию:
- чем она больше, тем неопределенности
выше.
Энтропия используется в социальной статистике в качестве меры неопределенности политической ориентации избирателей.
Пример: имеются данные о распределении голосовавших в двух районах области за кандидатов в местное законодательное собрание.
партия |
1-ый район (%) |
2-ой район (%) |
1) СПС |
10 |
6 |
2)Яблоко |
18 |
12 |
3)ЛДПР |
5 |
7 |
4) КПРФ |
20 |
24 |
5)Единая Россия |
47 |
51 |
Итого |
100 |
100 |
В каком районе выше степень неопределенности ориентации избирателей?
Виды дисперсий в совокупности, разделенной на группы. Правила сложения дисперсий.
Если данные представлены в виде аналитической группировки, то можно вычислить следующие виды дисперсий:
1)
- общая дисперсия,
2)
- межгрупповая дисперсия,
3)
- средняя из внутригрупповых дисперсий.
Общая дисперсия – измеряет вариацию признака под влиянием всех факторов.
где
- среднее по всей совокупности.
Межгрупповая дисперсия – характеризует вариацию признака, возникающую под влиянием группировочного признака.
,
- среднее по j-ой группе.
Внутригрупповая дисперсия
– отражает часть вариации, вызванную
влиянием неучтенных факторов и зависящую
от неучтенных признаков.
Теорема о сложении дисперсий:
Эмпирический коэффициент детерминации:
- показывает, какая доля общей дисперсии
приходится на дисперсию, вызванную
группировочным признаком.
Эмпирическое корреляционное отношение:
,
Характеризует связь между группировочным и результативным признаками.
Если
,
то группировочный признак не влияет на
результативный.
Если
,
то результативный признак меняется
только под влиянием группировочного.
Выборочные наблюдения.
Выборочным называется такое не сплошное наблюдение, при котором признаки регистрируются у отдельных единиц совокупности. Полученные результаты с определенным уровнем вероятности распространяются на всю генеральную совокупность.
Отбор единиц в выборочную совокупность может быть повторным и бесповторным.
При повторном отборе, попавшая в выборку, единица подвергается регистрации, а затем возвращается в исходную совокупность и, наравне с другими единицами, участвует в дальнейшей процедуре отбора.
На практике повторный отбор обычно используется, если объем генеральной совокупности неизвестен.
Например, при проведении маркетинговых исследований – неизвестно, сколько покупателей делают покупки в данном магазине (один и тот же покупатель может попасть в выборку дважды).
При бесповторном отборе, попавшая в выборку единица, подвергается исследованию и в дальнейшей процедуре отбора не участвует.
Этот отбор используется, когда объем генеральной совокупности не известен, полученные при этом результаты являются более точными, чем при повторном исследовании.
Например, опрос учащихся в институте.
В выборочную совокупность могут отбираться не только отдельные единицы, но и группы единиц.
В первом случае отбор называется индивидуальным, а во втором – групповым.
Методы отбора единиц в выборочную совокупность.
Процесс формирования выборочной совокупности основан на принципе случайности. Наиболее простой метод обеспечения случайности, который часто используется на практике – метод прямой реализации.
Суть этого метода:
на первом этапе все единицы совокупности, распределенные в случайном порядке, нумеруются цифрами от 1 до N;
на втором этапе с помощью генератора случайных чисел получают n - значений в интервале от 1 до N;
на третьем этапе из сформировавшегося списка отбирают единицы, соответствующие по номеру полученным случайным числам.