Тема 1. Концептуальні аспекти математичного моделювання економіки

Для забезпечення успішної діяльності підприємства під час планування виробничої програми, проведення фінансового контролінгу тощо доцільно використовувати економіко-математичні методи, які поєднують в собі математику, економіку та інформаційні технології. Економіко-математична модель – це опис економічного процесу чи явища у вигляді математичних функцій, нерівностей і рівнянь з метою його дослідження і управління. Економіко-математичні моделі поділяються на такі групи:

- оптимізаційні, які дозволяють обрати найкраще рішення серед декількох можливих;

- економетричні, які присвячені аналізу взаємозв’язку певних явищ і процесів та складанню прогнозів;

• балансові, що узгоджують відповідність ресурсів і потреб у них, доходів і витрат тощо;

• сітьові, які дають можливість закріпити певні роботи за виконавцями.

Основні етапи економіко-математичного моделювання:

1. Аналіз економічної системи та постановка проблеми;

2. Розробка математичних моделей з урахуванням особливостей системи;

3. Реалізація параметрів моделі;

4. Перевірка адекватності моделі, коректування параметрів моделі та системи;

5. Аналіз отриманих результатів та прийняття відповідних рішень.

Питання для самостійного вивчення:

- принципи моделювання;

- якість моделі;

- класифікація моделей (теоретико-аналітичні моделі, прикладні моделі, функціональні моделі, структурні моделі, дескриптивні моделі, нормативні моделі, детерміновані моделі, стохастичні моделі, статичні моделі, динамічні моделі, лінійні моделі, нелінійні моделі).

Тема 2. Оптимізаційні економіко-математичні моделі

На практиці часто трапляються ситуації, коли потрібно обрати економічне рішення, найкраще з точки зору певного критерію в умовах жорстких обмежень. Такі задачі називаються оптимізаційними. Метою їх є знайти такі значення змінних, щоб цільова функція набувала оптимального (максимального чи мінімального) значення.

Область математики, яка присвячена теорії і методам розв’язування задач оптимізації називається математичним програмуванням.

Починати розв’язування оптимізаційних задач слід з побудови економіко-математичної моделі.

Приклад 2.1

Підприємство виготовляє деталі, які мають пройти послідовну обробку на трьох верстатах. Час використання першого верстата – 6 год., другого – 8 год., третього – 10 год. Тривалість обробки деталей наведено в табл. 2.1:

Таблиця 2.1

Тривалість обробки деталей, хв., за верстатами

Деталь	Верстат
	1	2	3
А	20	8	12
В	15	18	14

Прибуток від реалізації однієї деталі кожного виду становить відповідно 30 та 40 у. о. Визначити оптимальні добові обсяги виробництва деталей кожного виду, що максимізують її прибуток.

Записати економіко-математичну модель.

Розв’язання

По-перше, треба визначити, що брати за невідомі.

Шуканими величинами у цій задачі є оптимальні обсяги виробництва деталей А та В. Позначаємо їх за x₁ та х₂. За умовою потрібно максимізувати загальний прибуток, який визначається як добуток прибутку від реалізації однієї деталі на їх кількість. Тому цільова функція (загальний прибуток, який прямує до максимуму), знаходиться за формулою 30x₁+ 40х₂ → max.

Можливі обсяги виробництва деталей обмежуються максимальним часом роботи верстатів. Перший верстат використовується 20x₁+ 15х₂ хв., але не більше 6 год (360 год.). Таким чином, 20x₁+ 15х₂ ≤ 360. Аналогічно знаходимо обмеження за другим та третім верстатами:

8x₁+ 18х₂ ≤ 480;

12x₁+ 14х₂ ≤ 600.

Обсяги виробництва деталей не можуть бути від’ємними, тому x₁≥0 та x₂≥0.

Отже, економіко-математична модель задачі прийме вигляд:

30x₁+ 40х₂ → max

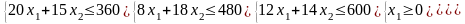
Отриману модель можна розв’язати за допомогою пошуку рішення в Excel, симплекс-методом або графічно.

Зустрічаються також оптимізаційні задачі, коли цільова функція прямує до мінімуму. Наприклад, потрібно знайти мінімальну собівартість продукції, визначити найменшу вартість перевезення тощо.

Питання для самостійного вивчення: задача визначення оптимального розподілу виробничих потужностей, задача про розкрій, задача про дієту, задача про призначення, задача комівояжера, задача оптимального розподілу капіталовкладень.