
- •Поняття границі функції
- •Формули диференціювання
- •Диференціал функції
- •Основні правила диференціювання.
- •Похідні та диференціали вищих порядків
- •Дослідження функції та побудова графіка
- •Невизначений інтеграл
- •Основні методи інтегрування.
- •Безпосереднє інтегрування[ред. • ред. Код]
- •Метод підстановки (заміни змінної)[ред. • ред. Код]
- •Метод інтегрування частинами[ред. • ред. Код]
- •Інтегрування раціональних дробів[ред. • ред. Код]
- •Інтегрування раціональних дробів. Методика
- •Універсальна тригонометрична підстановка
Дослідження функції та побудова графіка
Загально відомою є схема дослідження функції для побудови графіка:
1) знайти область визначення функції та множину її значень;
2) дослідити функцію на парність та непарність, періодичність;
3) знайти точки перетину графіка функції з осями системи координат, точки розриву, проміжки знакосталості функції;
4) дослідити поводження функції біля точок розриву та на нескінченності, знайти якщо вони є, асимптоти графіка;
5) знайти нулі та точки розриву похідної, інтервали монотонності функції, точки екстремуму та екстремальні значення функції;
6) знайти нулі та точки розриву другої похідної, інтервали опуклості графіка функції, точки перегину та значення функції в цих точках;
7) для побудови графіка необхідно знайти достатню кількість контрольних точок, через які він проходить.
Зауважу, що на практиці не завжди є потреба досліджувати функцію за наведеною схемою і в такій саме послідовності.
Так, наприклад, множину значень деяких функцій можна встановити лише після знаходження екстремальних значень функції та її поводження біля точок розриву і на нескінченності.
Можна спочатку знайти нулі функції. Якщо вони розташовані не симетрично відносно нуля, то функція не може бути ні непарною, ні парною, ні періодичною. Такий же висновок можна зробити у випадку, коли функція має область визначення не симетричну відносно нуля, то, зрозуміло, що з такого факту ми не можемо робити висновок про парність або непарність. Проте, якщо нулі функції симетричні відносно нуля, але їх число скінчене, то вона не є періодичною.
Не може бути функція ні парною, ні непарною, ні періодичною, якщо нулі першої або другої похідних розміщені несиметрично відносно нуля.
Зручно користуватися такими твердженнями:
1. сума скінченого числа парних (непарних) функцій є парною (непарною) функцією;
2. добуток парних функцій є парною функцією;
3. добуток непарних функцій є парною функцією, якщо число функцій-множників – парне число, і непарною, якщо число функцій-множників непарне;
4. добуток(частка) парної і непарної функції є функцією непарною.
Невизначений інтеграл
Означення.
Якщо F(x)
– первісна f(x),
x є І, то
вираз F(x)+с,
де с – будь-яке число
називається невизначеним інтегралом
функції f(x)
(або виразу f(x)dx)
і записується
 .
.
Вираз
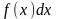 називається підінтегральним виразом,
називається підінтегральним виразом,
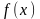 називається підінтегральною функцією.
називається підінтегральною функцією.
Приклад.
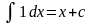 ,
,
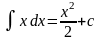 ,
,

Властивості невизначених інтегралів
1.
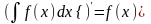 - операція інтегрування і взяття похідної
взаємно обернені.
- операція інтегрування і взяття похідної
взаємно обернені.
2.
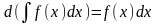 і
і
 ,
значки
,
значки
 і
d взаємно
скорочуються .
і
d взаємно
скорочуються .
3.
 .
.
4.
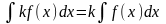 .
.
5. Оскільки формула для
диференціалу
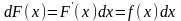 інваріантна відносно х і значки
інваріантна відносно х і значки
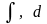 взаємно скорочуються то, взявши з обох
боків інтеграли отримаємо, що формула
для інтеграла має таку ж властивість,
тобто
взаємно скорочуються то, взявши з обох
боків інтеграли отримаємо, що формула
для інтеграла має таку ж властивість,
тобто
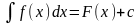 правильна і тоді коли х є внутрішня
функція, тобто
правильна і тоді коли х є внутрішня
функція, тобто
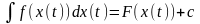
 ,
,
 .
.
Основні методи інтегрування.
1. Безпосереднє інтегрування.
2. Метод заміни змінної
3. Інтегрування по частинах.
Безпосереднім інтегруванням будемо називати інтегрування за допомогою властивостей невизначеного інтеграла, тотожних перетворень підінтегральної функції і таблиці основних інтегралів.
Приклад 1.
 .
.
В основі методу підстановки (або методу заміни змінної) обчислення невизначених інтегралів лежить таке твердження, яке є наслідком правила диференціювання складеної функції:
Нехай дано функції
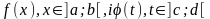 ,
і нехай існує складена функція
,
і нехай існує складена функція
 .
Якщо функція
має первісну
.
Якщо функція
має первісну
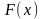 ,
а функція
,
а функція
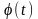 диференційована, то функція
диференційована, то функція
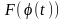 є первісною для функції
є первісною для функції
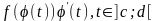 ,
і тому
,
і тому
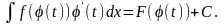
Приклад 1.
Обчислити інтеграл

Розв’язання.
Замінимо змінну
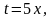 тоді
тоді
 ,
,
отже,
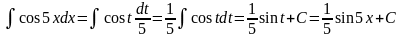 .
.
Приклад 2. Обчислити інтеграл
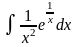 .
.
Розв’язання.
Припустимо, що
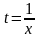 ,
тоді
,
тоді
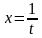 і
і
 .
Отже,
.
Отже,
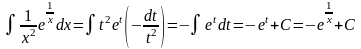 .
.
Інтегрування по частинах.
За правилом диференціювання добутку маємо
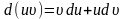 .
.
Тому
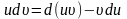
Якщо похідні (або, що те саме, диференціали) двох функцій рівні, то їх невизначені інтеграли збігаються. Тому
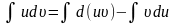
Використовуючи властивість невизначених інтегралів:
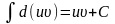 ,
,
дістанемо формулу
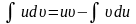 (1)
(1)
Цю формулу називають формулою інтегрування частинами.
Приклад 1. Обчислити
інтеграл
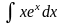
Розв’язання. Припустивши
 ,
,
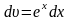 ,
,
тоді
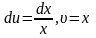
Звідси за формулою (1) матимемо
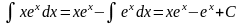
Приклад 2. Обчислити
інтеграл
 .
.
Розв’язання.
Припустимо, що
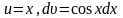
тоді

Тому, використовуючи формулу (1), маємо
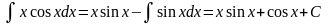
Використовуючи
формулу інтегрування частинами для
відшукання інтегралів від добутку,
важко дати загальне правило для визначення
того, який співмножник в підінтегральному
виразі слід позначити через
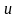 і який через
і який через
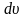 .
Водночас при визначенні інтегралів
необхідно, щоб
.
Водночас при визначенні інтегралів
необхідно, щоб
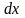 обов’язково входило у вираз для
і цей вираз був легко інтегрованим, а
також щоб інтеграл
обов’язково входило у вираз для
і цей вираз був легко інтегрованим, а
також щоб інтеграл
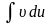 був простішим від вихідного. Так,
наприклад, для інтегралів виду
був простішим від вихідного. Так,
наприклад, для інтегралів виду
 ,
,
 ,
,
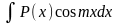 за
беруть многочлен
за
беруть многочлен
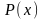 ,
а для інтегралів виду
,
а для інтегралів виду
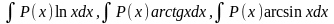 за
беруть відповідно
за
беруть відповідно
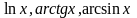
Якщо в інтегралах першого виду многочлен вищий від першого степеня, то формулу інтегрування частинами треба застосовувати кілька разів.
Приклад 3. Знайти
інтеграл

Розв’язання.
Припустимо, що
 і
і
 ,
тоді
,
тоді
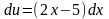 і
і
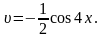 Тому
Тому
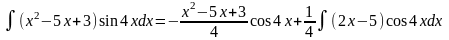

Останній інтеграл знайдемо інтегруванням частинами.
Припустимо тепер,
що
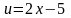 і
і
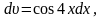 тоді
тоді
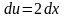 і
і
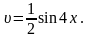 Отже,
Отже,
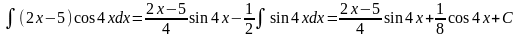
Таким чином,


Формула інтегрування частинами застосована і для знаходження інтегралів виду
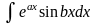 і
і
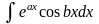 .
Для знаходження таких інтегралів формулу
інтегрування частинами застосовують
послідовно двічі, причому обидва рази
за
беруть або показникові функцію, або
тригонометричну. Після дворазового
інтегрування частинами дістають лінійне
рівняння відносно шуканого інтеграла.
.
Для знаходження таких інтегралів формулу
інтегрування частинами застосовують
послідовно двічі, причому обидва рази
за
беруть або показникові функцію, або
тригонометричну. Після дворазового
інтегрування частинами дістають лінійне
рівняння відносно шуканого інтеграла.
Приклад 4. Обчислити
інтеграл
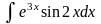
Розв’язання.
Припустимо, що
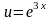 і
і
 ,
звідки
,
звідки
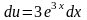 і
і
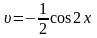 .
Тому
.
Тому
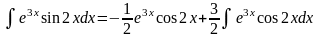 (2)
(2)
Для знаходження останнього інтеграла використаємо ще раз формулу інтегрування частинами:
і

і
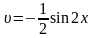
Тоді
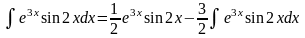
Підставивши цей вираз у рівність (2) дістанемо

Отже,
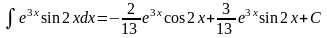
Точне знаходження первісної чи інтеграла для довільних функцій - справа значно складніша, ніж диференціювання, тобто пошук похідної. У загальному випадку подати інтеграл довільної функції в елементарних функціях часто просто неможливо. Тому існує набір методів для пошуку інтеграла окремих груп функцій.
