Поняття послідовності.

Якщо задана закономірність, згідно з якою кожному натуральному числу 1, 2, 3,…, відповідає деяке дійсне число, то говорять, що задана послідовність.

Послідовність можна розглядати як функцію, областю визначення якої є множина натуральних чисел. Послідовність визначається формулою, тобто законом, згідно з яким установлюється спосіб відповідності заданих чисел послідовним натуральним числам. Послідовність із загальним членом 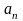позначається або просто .

Границя послідовності

Означення. Число а називається границею послідовності , якщо для кожного як завгодно малого додатного числа 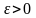знайдеться таке натуральне число 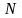, що при всіх 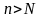виконується нерівність: .

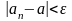Той факт, що число а є границею послідовності записується у вигляді:

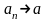, або , якщо .

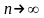Зауважимо, що нерівність рівносильна нерівностям:

, або .

Це означає, що число належить інтервалу 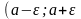). Такий інтервал називається 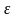- околом точки а.

Означення границі послідовності можна перефразувати наступним чином, надавши йому геометричну наочність: число а називається границею послідовності , якщо в будь-який - окіл числа а попадуть всі члени послідовності, починаючи з деякого номера, яким би вузьким цей окіл не був. Поза - околом може бути скінченне число членів даної послідовності.

Дійсно, якщо при , то для будь-якого знайдеться таке число N, що всі члени послідовності з номерами знаходиться в -околі числа а, поза цим околом можуть знаходитьсь тільки перших N членів послідовності.

Послідовність називається монотонно зростаючою (спадною), якщо .

Послідовність називається обмеженою зверху, якщо існує число m, таке, що при всіх n=1,2,3,…. Виконується нерівність .

Послідовність називається обмеженою знизу, якщо існує число m, таке, що при всіх n=1,2,3,…. Виконується нерівність .

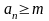Послідовність 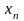не обмежена зверху або знизу, називається необмеженою.

Послідовність, що має границю, називається збіжною, а яка не має границі, називається розбіжною.

сновні властивості границь послідовності :

Якщо послідовності   і   мають границі, то:

Поняття границі функції

Нехай функція  визначена у всіх точках проміжку  , за винятком, можливо, деякої точки  . Побудуємо послідовність значень аргументу функції  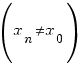: ,     (1) таку, щоб всі члени послідовності належали проміжку  і послідовність збігалась до точки  : . Тоді значення функції 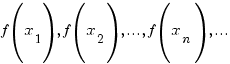 . (2) також утворять деяку числову послідовність. Говорять, що число  є границею функції  при  , що прямує до  , якщо для будь-якої послідовності значень аргументу (1), яка збігається до числа  , послідовність значень функції (2) збігається до числа  , і пишуть . Примітка. Це визначення границі функції називається визначенням границі по Гейне. Існує й інше, еквівалентне тому, що вище, визначення границі функції. Говорять, що число  є границею функції  при  , що прямує до  , якщо для будь-якого додатнього числа  знайдеться таке додатне число  , яке залежить від  , що при всіх  , які задовільняють нерівність , виконується нерівність . Примітка. Це визначення границі функції називається визначенням границі по Коші.

Границя (ліміт, lim) - це основа для вивчення похідних, невласних інтегралів, пошуку асимптот функції, її поведінки поблизу точок розриву і т.д. Розглянемо основні властивості границь, які використовуються прирозв'язанні задач і контрольних.

Границя суммы

Границя суми скінченого числа функцій дорівнює сумі границь доданків (якщо кожна з них існує) 

Границя добутку

Границя добутку скінченого числа функцій дорівнює добутку границь множників (якщо кожна з них існує)    Звідси - наступні дві властивості.

Границя добутку функції на константу

Постійний множник можна винести за знак границі 

Границя функції в натуральному ступені

Границя функції в натуральному ступені дорівнює натуральному ступеню від границі функції 

Границя відношення (дробу)

Границя відношення функцій дорівнює відношенню границь (якщо кожна з них існує і при цьому границя знаменника не дорівнює нулю) 

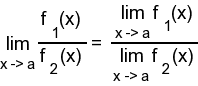
приклад перетворення границі

Спочатку границю відношення розглядаємо як відношення границь, потім кожну границю суми розглядаємо як суму границь і т.д. 

Похідною функції ƒ у точці x₀ називається границя, до якої прямує відношення

,

якщо Δx наближається до нуля.

Отже,

.

Функція, яка має похідну в точці x₀, називається диференційованою в цій точці.

Поняття похідної та диференційованості функції в точці є тотожними. Тому часто операцію знаходження похідної називають диференціюванням функції.

Формули диференціювання

c′ = 0, де c – константа (число)

(x)′ = 1

(x^k)′ = k · x^k-1

(sin x)′ = cos x

(cos x)′ = - sin x

(tg x)′ = 1 ⁄ cos²x

(ctg x)′ = - 1 ⁄ sin²x

(e^x)′ = e^x

(a^x)′ = a^x · ln(a)

(log_ax)′ = 1 ⁄ (x·ln(a))

(ln(x))′ = 1 ⁄ x

Якщо u(x) і v(x) деякі функції, то: