55. Понятие о множественной корреляции.

Корреляционная связь (частный случай стохастической) – связь, проявляющаяся при достаточно большом числе наблюдений в виде определенной зависимости между средним значением результативного признака и признаками-факторами.

Различают: парную корреляцию – это зависимость между результативным и факторным признаком;

частную корреляцию – это зависимость между результативным и одним факторным признаком при фиксированном значении других факторных признаков;

множественную – многофакторное влияние в статической модели

.

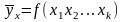Множественный коэффициент корреляции в случае зависимости результативного признака от двух факторов вычисляется по формуле:

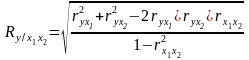, (5.20)

где 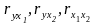– парные коэффициенты корреляции между признаками.

Множественный коэффициент корреляции изменяется в пределах от 0 до 1 и по определению положителен: .

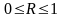Значимость коэффициента множественной детерминации, а соответственно и адекватность всей модели и правильность выбора формы связи можно проверить с помощью критерия Фишера:

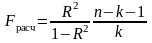, (5.21)

где R² – коэффициент множественной детерминации (R² );

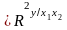k – число факторных признаков, включенных в уравнение регрессии.

Связь считается существенной, если F_расч > F_табл – табличного значения F-критерия для заданного уровня значимости α и числе степеней свободы ν₁ = k, ν₂ = n – k – 1.

54. Понятие криволинейной зависимости, оценка тесноты связи при криволинейной зависимости.

Корреляционная связь проявляется, когда одному и тому же значению факторного признака соответствует ряд значений признака-результата, причем связь обнаруживается в виде тенденции изменения среднего значения результативного признака в зависимости от изменения факторного признака. Это свободная и неполная связь.

Если происходит неравномерное изменение явления в связи с изменением величины влияющего фактора, то такая связь называется криволинейной. Математически криволинейная зависимость может быть выражена уравнением криволинейной связи. В экономическом анализе для ее выражения часто пользуютсяуравнением параболы второго порядка:  

.

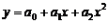Уравнение криволинейной связи может быть выражено и в виде гиперболической функции: 

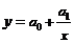
Для оценки тесноты криволинейной корреляции служит выборочное корреляционное отношение 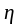_ух, которое далее будем обозначать через η и для простоты речи называть корреляционным отношением.

Связь тем сильнее, чем больше .

Корреляционное отношение удовлетворяет двойному неравенству:

• 0 ≤ η ≤ 1. (6.37)

Если η = 0, то переменная Y с переменной X корреля­ционной зависимостью не связана.Если η = 1, то переменная Y связана с переменной X функ­циональной зависимостью Выборочное корреляционное отношение не меньше абсолютной величины выборочного коэффициента корре­яции:

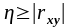• . (6.38)

При криволинейной зависимости Y от Х для оценки той доли вариации зависимой переменной Y, которая определяется влиянием независимой переменной Х, следует употреблять индекс детерминации 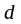, величина которого может быть выражена так:

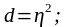(6.39)

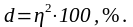(6.40)

Корреляционное отношение η служит мерой тесноты корреляционной связи любой формы, в том числе и линейной.